Цель и объем курсового проекта

Злобина И.В., Бекренев Н.В.

КУРСОВОЕ ПРОЕКТИРОВАНИЕ ПО ДИСЦИПЛИНАМ

«Детали машин» и «Детали машин и основы конструирования»

для направлений: 15.03.02 - Технологические машины и оборудование,

15.03.05 - Конструкторско-технологическое обеспечение машиностроительных производств

23.03.03 - Эксплуатация транспортно-технологических машин и комплексов

(учебное пособие)

для студентов всех форм обучения

Одобрено ученым советом

Института электронной техники

и машиностроения СГТУ

имени Гагарина Ю.А.

от «___» декабря 2015 г. № ___

Саратов 2015

Рецензенты

Кафедра «Технология машиностроения»

Пензенский государственный университет

д.т.н., профессор Загородских Б.П.

Саратовский аграрный университет имени Н.И. Вавилова

Злобина И.В. Учебное пособие по выполнению курсового проекта по дисциплинам

«Детали машин» и «Детали машин и основы конструирования» / И.В. Злобина, Н.В. Бекренев. – учебное пособие для студентов направлений 15.03.02 - Технологические машины и оборудование, 15.03.05 - Конструкторско-технологическое обеспечение машиностроительных производств и 23.03.03 - Эксплуатация транспортно-технологических машин и комплексов . – Саратов: Сарат. гос. техн. ун-т, 2016.- с.

В пособии на основе обобщения методик расчетов и рекомендаций по расчету и конструированию деталей машин и механизмов изложена последовательность проектирования механического привода, состоящего из одноступенчатого редуктора и открытой передачи. Приведен алгоритм автоматизированного расчета одноступенчатого цилиндрического редуктора и открытых передач разных типов в CAD/CAE программной среде APM Winmachine. Приведены таблицы с необходимыми для проектирования справочными данными, что позволяет использовать для выполнения курсового проекта только данное пособие без обращения к другим источникам информации. В приложении приведены примеры оформления чертежей типовых редукторов и их элементов, а также примеры определения исходных данных для проектирования механических передач некоторых наиболее распространенных технологических и транспортных машин.

Пособие предназначено для студентов всех форм обучения, изучающих дисциплины «Детали машин» и «Детали машин и основы конструирования» и может быть полезно также при выполнении практических заданий по СРС.

© Саратовский государственный

технический университет

имени Гагарина Ю.А.

© Злобина И.В., Бекренев Н.В.

Содержание

		Стр.
	Цель и объем курсовой работы. Требования к оформлению
	1.1 Цель и объем курсовой работы
	1.2 Требования к оформлению пояснительной записки и графических материалов.
	1.3 Порядок отчета по выполнению курсовой работы
	Основные сведения о редукторах исполнительных механизмов технологических и транспортных машин
	Кинематический расчет и выбор электродвигателя
	Расчет зубчатых колес редуктора
	4.1 Расчет цилиндрических колес с прямыми и наклонными зубьями
	4.2 Особенности расчета конических колес
	4.3 Особенности расчета червячной передачи
	Предварительный расчет валов. Конструирование валов
	Первый этап компоновки редуктора
	Определение конструктивных размеров зубчатых колес
	Определение размеров конструктивных элементов корпуса редуктора
	Расчет внешней передачи
	9.1 Расчет цепной передачи
	9.2 Расчет ременной передачи
	9.3 Расчет винтовой передачи
	9.4 Расчет открытой зубчатой передачи
	Проверка долговечности подшипников
	Второй этап компоновки редуктора
	Проверка шпоночных соединений
	Уточненный расчет валов
	Выбор типа смазки (сорта масла) и определение ее объема
	Особенности разработки сборочного чертежа редуктора
	Разработка общего вида привода
	Последовательность расчета одноступенчатого цилиндрического редуктора в CAD/CAE программной среде APM Winmachine
	Последовательность расчета клиноременной передачи в CAD/CAE программной среде APM Winmachine
	Последовательность расчета плоскоременной передачи в CAD/CAE программной среде APM Winmachine
	Последовательность расчета цепной передачи в CAD/CAE программной среде APM Winmachine
	Последовательность расчета винтовой передачи в CAD/CAE программной среде APM Winmachine
	Литература
	Приложения
	Форма титульного листа пояснительной записки
	Электродвигатели асинхронные обдуваемые в алюминиевом корпусе
	Подшипники шариковые радиальные
	Подшипники шариковые радиально-упорные
	Подшипники конические роликовые
	Пример оформления сборочного чертежа цилиндрического редуктора
	Пример оформления сборочного чертежа конического редуктора
	Пример оформления сборочного чертежа червячного редуктора
	Пример оформления рабочего чертежа вала
	Пример оформления цилиндрического вала-шестерни
	Пример оформления рабочего чертежа цилиндрического зубчатого колеса
	Пример оформления рабочего чертежа конического вала-шестерни
	Пример оформления рабочего чертежа конического колеса
	Пример определения исходных данных для расчета привода винтового пресса
	Пример определения исходных данных для расчета привода плоскодоводочного станка
	Пример определения исходных данных для расчета коробки подач вертикально-сверлильного станка
	Пример определения исходных данных для расчета привода лебедки автоэвакуатора
	Пример определения исходных данных для расчета привода гаражного подъемника
	Пример определения исходных данных для расчета привода кантователя

1. Цель и объем курсового проекта. Требования к оформлению

И наклонными зубьями

Так как к большинству транспортных и технологических машин общего назначения не предъявляется особых требований в отношении габаритов передачи, можно выбрать материалы со средними механическими характеристиками: для шестерни - сталь 45, термическая обработка — улучшение (твердость НВ 230-260); для колеса — сталь 45, термическая обработка – улучшение (твердость на 30 единиц ниже: НВ 200-230). При больших передаточных числах для шестерни необходимо принять в качестве термической обработки закалку. В случае проектирования передач энергетических машин, или металлорежущих станков, а также двигателей летательных аппаратов и судовых приводов необходимо выбирать легированные стали. Характер термической обработки определяется также условиями работы передачи. При больших окружных скоростях, когда велики контактные напряжения и износ поверхности, а также в случае ударных нагрузок, лучше применять поверхностную закалку или химико-термическую обработку с целью сохранения относительно вязкой сердцевины, обеспечивающей требуемые упруго пластические характеристики. При значительных вращающих моментах, когда велики изгибные напряжения, но при относительно спокойном характере нагрузки требуется объемная закалки для повышения общей прочности зуба.

Допускаемые контактные напряжения находятся из выражения [14]:

σ_H =σ_HlimbK_HL / [S_H] ,

где σ_Hlimb - предел контактной выносливости при базовом числе циклов, выбираемый по табл. 4.1. [13].

Расчеты проводят для шестерни и колеса.

Таблица 4.1 Пределы контактной σ_Hlimb и изгибной σ_Flimb выносливости в зависимости от материала зубчатого колеса и его термообработки

Способ ТО или ТХО зубьев	Сталь	Твердость	σHlimb, Н/мм2	σFlimb, Н/мм2
Отжиг, нормализация, улучшение	Углеродистая	< HB 350	2HB+70	HB+260
Объемная закалка	Углеродистая	HRC 38…55	18HRC+150	550-600
Цементация	Легированная	HRC 32…64	23HRC	750-850
Азотирование	Легированная	HV 550…750	1,5HV	-
Азотирование	Легированная	HRC 23…42	-	19HRC+43

K_HL — коэффициент долговечности; при числе циклов нагружения больше базового, что имеет место при длительной эксплуатации редуктора, принимают K_HL = 1 ; коэффициент безопасности [SH] = 1,10 -1,15.

Для косозубых колес расчетное допускаемое контактное напряжение равно:

[σ_H] = 0,45([σ_H1] + [σ_H2])

где [σ_H1] - для шестерни; [σ_H2] - для колеса.

Для прямозубых колес пределы контактной выносливости рассчитывают раздельно для шестерни и колеса по выражению [14]:

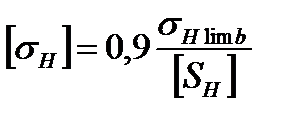
Затем для дальнейших расчетов принимают меньшее значение.

В обоих случаях (для косозубой и прямозубой передачи) должно выполняться условие [σ_H] < 1,23 [σ_H2].

Для дальнейших расчетов определяется коэффициент ширины венца по межосевому расстоянию ψ_ba = b /a_W из следующего ряда значений: 0,1; 0,125; 0,16; 0,2; 0,315; 0,4; 0,5; 0,63; 0,8; 1,0; 1,25. При этом учитывают, что для редукторов общего назначения ψ_ba = 0,2-0,63, для коробок скоростей ψ_ba = 0,1-0,16.

Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев определяется по формуле [14]:

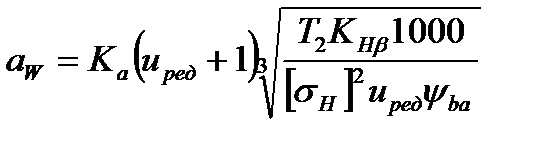
где для косозубых колес К_а = 43, а для прямозубых К_а = 49,5; u_ред – передаточное число редуктора.

Значение коэффициента K_Hβ может быть определено с учетом симметричности расположения колеса на валу редуктора и влияния внешней передачи по табл. 4.2. [13]. Предварительно рассчитывается коэффициент ширины зубчатого венца по диаметру ψ_bd.

Таблица 4.2 Коэффициент симметричности расположения зубчатых колес на валу редуктора относительно опор K_Hβ

Твердость НВ	Коэффициент ширины зубчатого венца ψbd=0,5 ψba(u+1)
0,2	0,4	0,6	0,8	1,0	1,2
Консольное расположение шестерни или колеса
< 350	1,05-1,08	1,12-1,18	1,2-1,3	1,27-1,45	-	-
>350	1,1-1,22	1,25-1,44	1,45	-	-	-
Колеса сдвинуты к одной из опор
< 350	1,02	1,03-1,05	1,04-1,07	1,05-1,12	1,07-1,15	1,1-1,2
>350	1,02-1,05	1,05-1,12	1,08-1,2	1,14-1,28	1,2-1,37	1,25-1,47
Колеса расположены в средней части вала
<350	1,01	1,02	1,025	1,025-1,03	1,03-1,05	1,04-1,06
>350	1,01	1,02	1,025-1,05	1,03-1,07	1,06-1,12	1,08-1,16

Если на валу имеется внешняя передача, то даже при расположении шестерни и колеса в средней части вала в редукторе необходимо принимать K_Hβ как для случая консольного расположения колеса

Полученное значение межосевого расстояния округляется по ГОСТ 2185-81 (желательно из первого ряда чисел) в сторону большего ближайшего значения: a_w = 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400, 500, 630, 800, 1000, 1250, 1600, 2000, 2500.

Модуль зацепления (нормальный модуль для косозубых колес) принимается по следующей рекомендации [13]: m=m_п = (0,01 - 0,02) a_w.

Полученное значение округляется в большую сторону по ГОСТ 9563 — 80: 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; 50.

Число зубьев шестерни определяется из соотношений:

- для прямозубых колес ,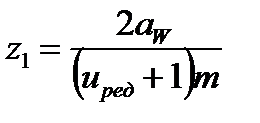

- для косозубых колес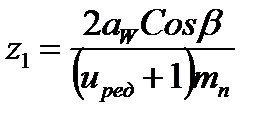

Угол наклона зубьев во избежание больших осевых усилий обычно принимают равным β = 8-15⁰. В исключительных случаях увеличивают угол до 20⁰. Предварительно угол наклона зубьев для определения их числа на шестерне и колесе принимают равным β = 10° .

Минимальное число зубьев на шестерне без подрезания ножки и коррегирования составляет z₁ = 17. Рекомендуют для первой ступени редуктора z₁ = 22-36, для второй и последующих ступеней z₁ = 18-26.

Число зубьев колеса z₂ = z₁ u_ред. Полученное значение округляют до ближайшего целого числа. Проводят проверку фактического передаточного числа: u_Ф = z₂ / z₁. Отклонение фактического передаточного числа от номинального значения не должно превышать 2,5% при u < 4,5 и 4% при u > 4,5.

Уточненное значение угла наклона зубьев с учетов фактического их количества для косозубой передачи определяется из выражения:

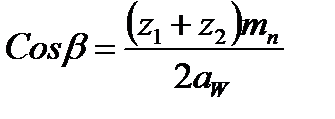
Далее определяются основные размеры шестерни и колеса:

диаметры делительные (колеса с наклонными зубьями):

d₁=m_n z₁ / cosβ;
d₂=m_n z₂ / cosβ.

диаметры делительные (колеса с прямыми зубьями):

d₁=m_n z₁;
d₂=m_n z₂ .

Проверка по определенному ранее межосевому расстоянию:

a_W = 0,5(d₁ + d₂).

диаметры вершин зубьев:

d_a1 = d₁ + 2m_n;
d_a2 = d₂ + 2m_п;

ширина колеса b₂ = Ψ_ba a_W;

ширина шестерни b₁ = b₂ + 5 .

Также следует учитывать что для более узкого колеса должно выполняться условие: b₂ < d₁ (для прямозубых колес), b₂ < 1,5d₁ (для косозубых колес).

Полученное значение ширины шестерни и колеса должно округляться в большую сторону по ряду чисел [13]: 16, 18, 20, 22, 25, 28, 32, 36, 40, 45, 50, 56, 63, 71, 80, 90, 100, 110, 125, 140, 160, 180, 200, 220.

Коэффициент ширины шестерни по диаметру: Ψ_bd = b₁ / d₁ .

Определение степени точности передачи производится в зависимости от окружной скорости, вида передачи и твердости зубьев [13] (Табл. 4.3).

Таблица 4.3 Степени точности зубчатых передач

Вид передачи	Форма зубьев	Твердость зубьев большего колеса, НВ	Степень точности по нормам плавности хода
6 высоко-точная	точная	8 средней точности	9 понижен-ной точности
Окружная скорость VO, м/с
Цилиндри-ческая	Прямые	< 350
>350
Непрямые	< 350
>350
Коничес-кая	Прямые	< 350
>350				2,5

Во избежание чрезмерно высоких коэффициентов нагрузки рекомендуется назначать степень точности на 1 выше, чем указано в данной таблице.

При этом сначала вычисляется окружная скорость колес по выражениям:
V₁ = 0,5 ω₁d₁ и V ₂ = 0,5 ω₂d₂. Вследствие известных кинематических соотношений V ₁ = V ₂. Затем выбирают в соответствии с типом передачи и твердостью зубьев ближайшее к расчетному значение скорости и по нему – степень точности колеса или шестерни.

Коэффициент нагрузки равен K_H = K_HβK_HaK_Hv

Значения K_Hβ находятся по табл. 4.2. Коэффициент K_Ha, учитывающий распределение нагрузки между зубьями, равен для прямозубых колес K_Ha =1, для косозубых колес выбирается в соответствии с табл. 4.4.

Таблица 4.4 Значения коэффициента K_Ha [13]

Степень точности	Коэффициент KHa при скорости V, м/с
	-	1,00	1,005	1,01	1,015	1,020
	1,002	1,007	1,025	1,04	1,05	1,06
	1,02	1,03	1,07	1,085	1,12	-
	1,05	1,09	1,13	-	-	-
	1,1	1,16	2,0	-	-	-

Коэффициент K_Hv учитывает динамическую нагрузку, возникающую в зацеплении. В расчетах передач общего назначения, не имеющих высоких требований к точности, принимают K_Hv = 1.

Проверка контактных напряжений производится по формуле [14]:

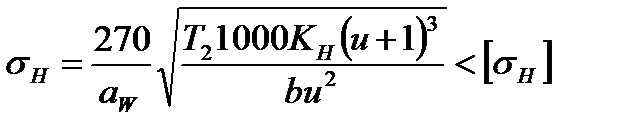
Силы, действующие в зацеплении (рис. 4.1), определяются из выражений:

- для прямозубых колес: окружная F_t = 2T₁ / d₁;
радиальная F_r = F_t tgα.
- для косозубых колес: окружная F_t = 2T₁ / d₁;
радиальная F_r = F_t tgα / cosβ;
осевая F_а = F_t tg β.

Ft Fr Ft Fr	Ft Fа Fа Ft Fr
а	б

Рис. 4.1 Силы, действующие в зацеплении прямозубых (а) и косозубых (б) колес

В этих выражениях α – стандартный угол зацепления, принятый в настоящее время во всех странах мира равным 20⁰. Проверка зубьев на выносливость по напряжениям изгиба производится по формуле [14]:

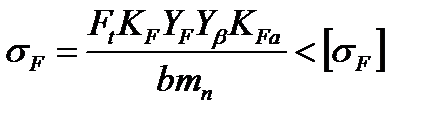
Здесь коэффициент нагрузки равен K_F = K_FβK_Fv.

K_Fβ =a K_Hβ,

где a = 1,2 приконсольном расположении шестерни на валу, a=1,15 при колесах, сдвинутых к одной из опор, a=1,1 при расположении колес в средней части вала.

K_Fv – коэффициент динамичности, зависящий от степени точности, твердости и формы зубьев, а также – вида зацепления и выбираемый по табл. 4.5 и 4.6 [13].

Таблица 4.5 Значения коэффициента K_Fv для прямозубых колес

Степень точности	Твердость зубьев большего колеса НВ	Окружная скорость, м/с
Цилиндри-ческие колеса	Коничес-кие колеса	< 1	1-3	3-8	8-12
	-	< 200		1,1	1,2	1,4
200-350		1,1	1,2	1,3
>350			1,2	1,3
		< 200		1,3	1,5	1,6
200-350		1,2	1,4	1,5
>350		1,2	1,3	1,4
		< 200	1,1	1,4	1,6	-
200-350		1,3	1,5	-
>350		1,3	1,4	-
		< 200	1,2	1,5	-	-
200-350	1,1	1,4	-	-
>350	1,1	1,4	-	-
-		< 200	1,3	1,6	-	-
200-350	1,2	1,5	-	-
>350	1,2	1,5	-	-

Таблица 4.6 Значения коэффициента K_Fv для косозубых колес

Степень точности	Твердость зубьев большего колеса НВ	Окружная скорость, м/с
2-3	3-8	8-12	12-18	18-25
	<350			1,1	1,2	1,3
>350				1,1	1,2
	<350			1,2	1,3	1,4
>350			1,1	1,2	1,3
	<350	1,1	1,3	1,4	-	-
>350	1,1	1,2	1,3	-	-
	<350	1,2	1,4	-	-	-

Y_F - коэффициент, учитывающий форму зуба и зависящий для косозубых колес от эквивалентного числа зубьев z_v, выбирается по табл. 4.7:

z_v1=z₁/cos³β; z_v2=z₂/cos³β.

Таблица 4.7 Значение коэффициента Y_F при коэффициенте смещения х=0

YF	-	-	4,28	4,09	3,9	3,8	3,7	3,65	3,62	3,61	3,6	3,6
zv (z)

Для прямозубых колес в таблице принимают вместо z_v z._. Коэффициент, учитывающий наклон зубаY_β равен для прямозубых колес Y_β = 1, для косозубых колес Y_β = 1 – (β / 140) ,

где β – угол наклона зубьев в градусах

Коэффициент, учитывающий распределение нагрузки между зубьями, K_Fa принимается для прямозубых колес равным K_Fa = 1, т.к. предполагается, что в зацеплении находится одна пара зубьев.

Для косозубых колес при определении K_Fa сначала рассчитывают коэффициент осевого перекрытия и проверяют условие:

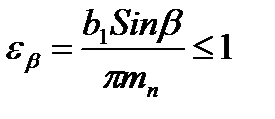
Если это условие выполняется, то принимают как для прямозубых колес K_Fa = 1. Если условие не выполняется, то коэффициент рассчитывают по зависимости:

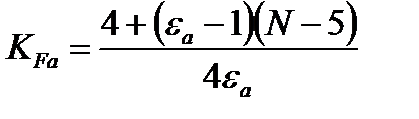
Где N – степень точности зубчатой передачи,

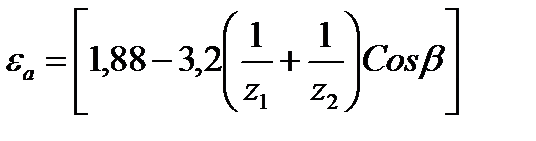- коэффициент торцового перекрытия

Допускаемые напряжения изгиба определяются по формулам [14]:

,

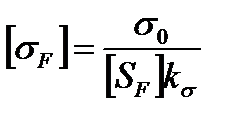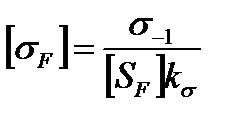
где σ₀ – предел выносливости материала колеса при отнулевом цикле (если передача не является реверсивной, и напряжения не отрицательные);

σ₀ = (1,4 – 1,6) σ_-1

σ_-1 – предел выносливости при симметричном цикле (если передача – реверсивная, напряжения - знакопеременные).
[S_F] – коэффициент безопасности (запаса прочности) по изгибным напряжениям, выбираемый из табл. 4.8.

Таблица 4.8 Значения коэффициента запаса прочности [S_F] [13]

Материал колес и метод термообработки	[SF]
Отливки стальные и чугунные без термообработки	1,9
Отливки стальные и чугунные с термообработкой	1,7
Поковки стальные нормализованные или улучшенные	1,5
Поковки стальные с объемной закалкой	1,8
Поковки и отливки с поверхностной закалкой (сердцевина вязкая)

k_σ – эффективный коэффициент концентрации напряжений у основания зуба, выбираемый по табл. 4.9.

Таблица 4.9 Значения коэффициента концентрации напряжений [13]

Материал колес и метод термообработки	kσ
Стальные нормализованные или улучшенные, а также с поверхностной закалкой	1,4-1,6
Стальные с объемной закалкой	1,8
Стальные азотированные, цементованные, цианированные и т.п.	1,2
Чугунные и пластмассовые	1-1,2

После расчета допускаемых напряжений для шестерни и колеса находят отношения [S_F] / Y_F . Проверка прочности зуба на изгиб производится для того элемента пары, у которого это отношение оказалось в результате расчета меньше.

Определение значения модуля

Ориентировочное значение модуля m можно определить, если, как и ранее, принять q = 0,25z₂, а межосевое расстояние а рассчитать по формуле, справедливой для передач без смещения исходного контура. Тогда имеем:

.

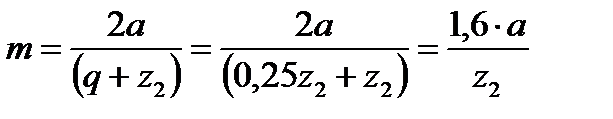Окончательно в качестве значения модуля выбирается ближайшая к рассчитанной величина из нормального ряда, приведенного ранее.

После определения основных геометрических параметров (a, m и z₂ ) необходимо уточнить коэффициент диаметра червяка q. Предварительно его вычисляют по формуле:

,

m

m

z

a

q

-

=

а затем в качестве коэффициента диаметра принимают ближайшее значение из ряда по ГОСТ 19672-74 (первый ряд предпочтительнее):

1-й ряд: 8,0; 10,0; 12,5; 16,0; 20,0; 25,0;

2-й ряд: 7,1; 9,0; 11,2; 14,0; 18,0; 22,4.

Округленным значениям a, m и q будет соответствовать передача со смещением:

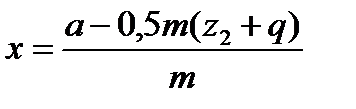
Диапазон допустимых значений коэффициента смещения х ограничен: -1 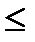х 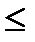1. Если при расчете это условие не выполняется, то следует варьировать параметры a, m и q до получения нужного значения х, принадлежащего указанному диапазону.

При наличии смещения делительный диаметр не совпадает с начальным. В дальнейшем для обозначения величин, связанных с начальным диаметром, используется индекс w.

Угол подъема винтовой линии на начальном диаметре:

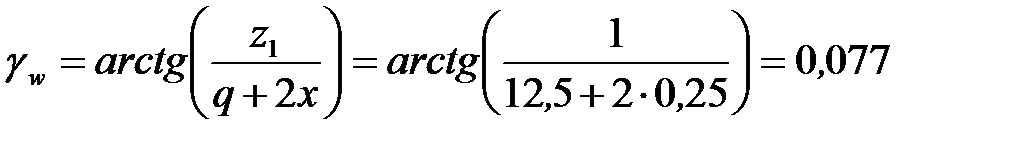
Делительный диаметр червяка

d₁ = mq .

Делительный диаметр червячного колеса

d₂ = mz₂ .

Начальный диаметр червяка

d_w1 = m (q+2x).

И изгибным напряжениям

Находим действующее напряжение в контакте витка червяка и зуба колеса:

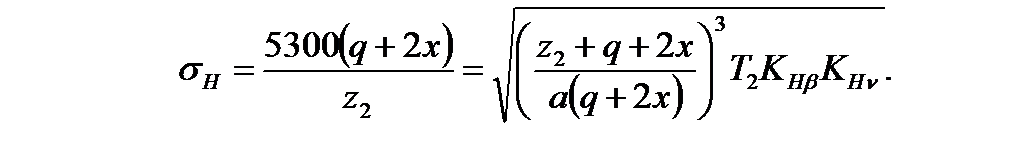
Сравнивая действующее напряжение с допускаемым,
σ_H<σ_Ha, убеждаемся в том, что условие прочности по контактным напряжениям выполнено.

Приведенное число зубьев

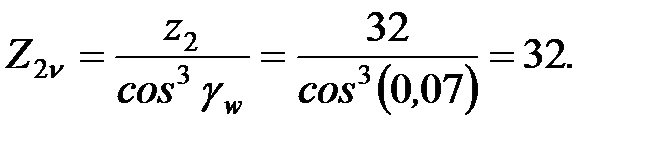
Окружная сила на колесе F_t2

Н.

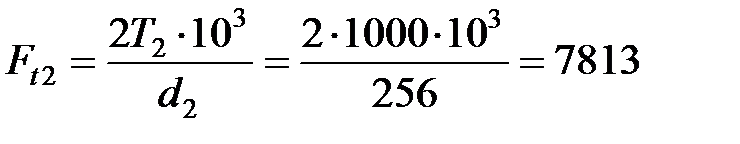
Значения коэффициентов концентрации К_Fβ и динамичности нагрузки К_Fν выбираем в соответствии с рекомендациями [13].

Коэффициент формы зуба для рассчитанного значения приведенного числа зубьев z_2ν выбирается по табл. 4.15.

Таблица 4.15 Коэффициенты формы зуба червячного колеса Y_F

zν	YF	zν	YF	zν	YF	zν	YF
	1,98 1,88 1,85 1,80		1,76 1,71 1,64 1,61		1,55 1,48 1,45 1,40		1,34 1,30 1,27 1,24

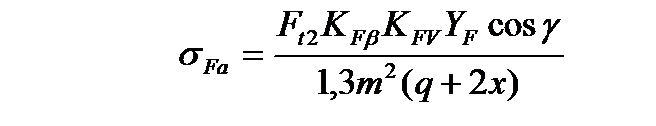
Силы в зацеплении

Окружная сила на колесе F_t2 и осевая на червяке F_a1

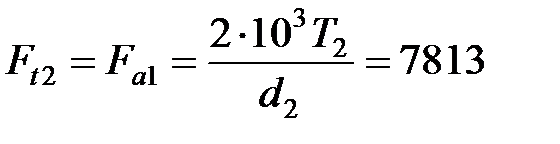
Окружная сила на червяке F_t1 и осевая на колесе F_а2

Н.

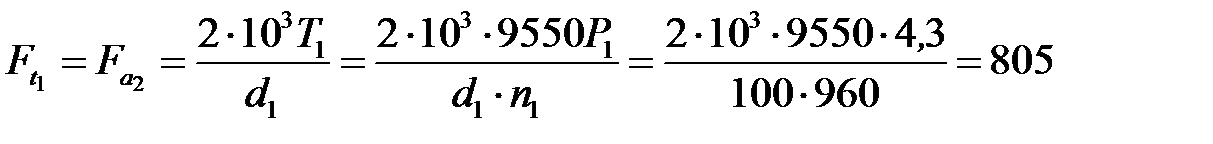
Радиальная сила в зацеплении

Н.

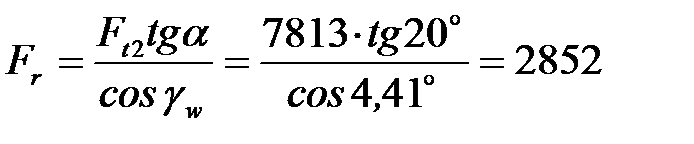
Предварительный расчет валов. Конструирование валов

Выбор материала вала

Валы изготавливают из углеродистых и легированных сталей. При отсутствии термообработки применяют Ст5, для термообработанных валов – стали 40, 45, 40Х. Для тяжелонагруженных валов ответственных машин используют качественные хромистые стали 40ХН, 40ХНМА, 30ХГТ. Быстроходные валы, установленные на подшипниках скольжения, изготавливают из цементованных сталей 20, 20Х, а особо быстроходные валы – из 12ХН3А, 18ХГТ.

Предварительное определение диаметров шеек вала

Предварительный расчет выходного конца вала проводят на кручение по пониженным допускаемым напряжениям:

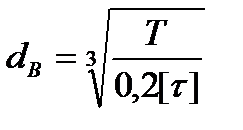
где Т – вращающий момент на валу, [τ] – допускаемые напряжения кручения, обычно принимаемые равными [τ]=20-35 Н/мм². Большие значения принимаются при использовании для изготовления колес легированных сталей.

По данной формуле рассчитывают диаметры выходных концов ведущего и ведомого валов. Однако, диаметр ведущего вала корректируется исходя из следующих соображений.

d1

dдв

dВ

dп

dп

Рис. 5.1 Вал-шестерня (ведущий вал)

Если вал редуктора соединен муфтой с валом электродвигателя, то необходимо согласовать диаметры вала двигателя d_дв и вала редуктора d_В. Как правило, принимают d_В = (0,7-1)d_дв. Некоторые муфты, например УВП, могут соединять валы разных диаметров в пределах одного номинального момента.

dшк

dп

dш

d2

dп

dВ

Рис. 5.2 Ведомый вал

Иногда вал электродвигателя не соединяется непосредственно с ведущим валом редуктора, а между ними имеется ременная или цепная передача (так приведено в ряде заданий на курсовое проектирование). В этом случае диаметр вала редуктора рекомендуется принимать равным диаметру вала двигателя или округлять расчетный диаметр в большую сторону до целого значения.

Валы обычно выполняют ступенчатыми с увеличением от концов к среднему сечению, т.к. в этом случае обеспечивается оптимальное сопротивление изгибу. Диаметры остальных шеек вала выбирают из следующих соображений.

1) Диаметр шеек под посадку подшипника выбирают по диаметру отверстия внутреннего кольца большим диаметра выходного конца вала с учетом того, что диаметры отверстий в кольцах подшипника, начиная с 20 мм кратны 5.

2) Диаметр шейки под зубчатым колесом d_ш определяют по выше приведенной формуле для нахождения диаметра выходной шейки вала, но величину касательных напряжений выбирают пониженной [τ]=10-20 Н/мм^2.

3) Для фиксации деталей (подшипников, шкивов и зубчатых колес) в осевом направлении служат буртики, высота которых ориентировочно принимается в зависимости от диаметра малой шейки:

d, мм	20-40	40-60	60-80	80-100
h, мм	3-5	5-8	7-9	7-10

4) Радиус галтели (переход от большего диаметра D к меньшему d) в тех местах, где нет посаженных на шейку деталей, выбирается из соотношений:

(D – d), мм	2-4	4-8	8-12	12-16	16-20
R, мм	1-2	2-3	3-5	4-7	5-8

5) При неподвижной установке на вал какой-либо детали (шкив, зубчатое колесо, звездочка) в месте упора детали в буртик последняя имеет фаску с катетом С, а вал - галтель радиусом R с выдерживанием соотношения C>R. Это обеспечивает плотное прилегание ступицы к буртику. Если на шейку с упором в буртик устанавливается подшипник, либо выполняют условие R₁ >R, где R₁ – радиус скругления (фаски) внутреннего кольца подшипника, либо на валу выполняют канавку для выхода шлифовального инструмента и обеспечения прилегания к буртику торца кольца подшипника. Последний случай предпочтительнее, поскольку обеспечивает более точную обработку цилиндрической и торцовой поверхностей вала независимо от износа кромки шлифовального круга.

Указанные параметры выбирают из соотношений:

d, мм	10-15	15-40	40-80	80-120
С, мм	1,5
R, мм		1,5		2,5

6) Размеры выходных концов валов могут быть приняты по рекомендациям, приведенным в [12].

Расчет внешней передачи

В большинстве редукторов общего назначения между редуктором и двигателем или между редуктором и рабочим органом машины устанавливаются открытые передачи. При этом на входе обычно применяются клино- или плоскоременные передачи, либо передачи отсутствуют и связь редуктора с валом двигателя осуществляется при помощи муфт различных типов. На выходе чаще всего устанавливают цепные, винтовые или зубчатые передачи.

Расчет цепной передачи

В ведущей ветви цепи в процессе стационарной работы передачи действует постоянная сила F₁, состоящая из окружной силы F_t и силы натяжения ведомой ветви F₂: F₁ = F_t + F₂.

Окружная сила на звездочках:

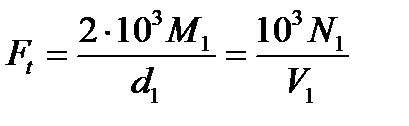
где М₁ - вращающий момент на ведущей звездочке,

d₁ - делительный диаметр ведущей звездочки,

N₁ - мощность на ведущей звездочке,

V₁ - скорость движения цепи.

Сила натяжения ведомой ветви: F₂ = F₀ + F_Ц

где F₀ - натяжение цепи от силы тяжести; F_Ц - натяжение от центробежных сил.

Натяжение от силы тяжести при горизонтальном (и близком к нему) положении линии, соединяющей оси звездочек, определяется как для гибкой нерастяжимой нити: .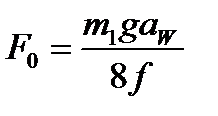

где m₁ - погонная масса цепи; g - ускорение свободного падения, a_W - межосевое расстояние; f - стрела провисания цепи.

При вертикальном (и близком к нему) положении линии центров звездочек: F₀ = m₁ g a_W

Натяжение цепи от действия центробежных сил определяют по аналогии с ременными передачами: F_Ц = m₁ V².

где V - скорость движения цепи.

Если ветви цепей параллельны, сила, действующая на валы равна F_Σ = F₁ + F₂.

Расчетная сила, действующая на валы передачи: F_Σ = k_B F_t.

где k_B - коэффициент, учитывающий вес цепи. Для горизонтальной передачи принимают k_B = 1,15; для вертикальной передачи k_B = 1,05.

Предварительный расчет начинают с определения величины статической разрушающей силы проектируемой цепи:

F_P^/ = F_t S

где S - коэффициент безопасности, зависящий от степени ответственности передачи, точности определения действующих наг