Ненапряженные и напряженные резьбовые соединения
В зависимости от назначения и условий сборки резьбовые соединения бывают ненапряженные (не затянутые в процессе сборки) и напряженные, загруженные осевой нагрузкой в процессе сборки до приложения внешней нагрузки.
Ненапряженное соединение
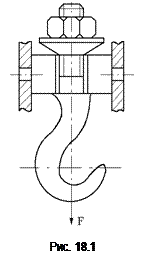
Примером может служить подвеска крюка подъемного крана (рис. 18.1). Такие соединения способны воспринимать только статическую нагрузку. Опасным будет сечение, ослабленное резьбой. Статическая прочность стержня с резьбой выше (в среднем на 10%), чем гладкого стержня с диаметром, равным внутреннему диаметру d1. Поэтому за расчетный диаметр dp принимают диаметр больше d1, а именно
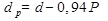 ,
,
где Р – шаг резьбы.
Из условия прочности 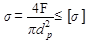
находим расчетный диаметр 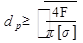 .
.
 Расчет затянутого болта при отсутствии внешней нагрузки
Расчет затянутого болта при отсутствии внешней нагрузки
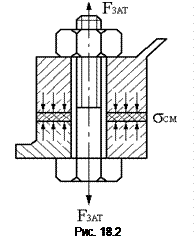
Примером может служить болт для крепления герметичных крышек и люков корпусов (рис. 18.2). В этом случае стержень болта растягивается осевой силой Fзат и закручивается моментом сил трения в резьбе Тр. Момент трения на торце гайки через стержень винта не передается.
Напряжение растяжения от усилия затяжки
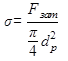 . (18.1)
. (18.1)
Напряжение кручения от момента трения в резьбе
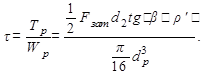 (18.2)
(18.2)
В этих формулах величина силы затяжки Fзат=Ssсм,
где S – площадь стыка детали; sсм – напряжение смятия в стыке деталей, величину которого выбирают по условиям герметичности.
Прочность болта определяют по эквивалентному напряжению (энергетическая теория)
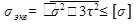 (18.3)
(18.3)
Подставим уравнения (18.1) и (18.2) в выражение (18.3)
 ,
,
откуда
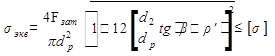
или
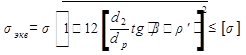 .
.
Принимая для стандартных стальных болтов с метрической резьбой b=2°30¢, 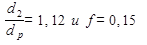 , чему соответствует r=8°40¢, окончательно получим
, чему соответствует r=8°40¢, окончательно получим 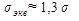 .
.
Следовательно, болт, работающий одновременно на растяжение и кручение, можно рассчитывать только на растяжение по допускаемому напряжению на растяжение, уменьшенному в 1,3 раза, или по расчетной силе, увеличенной по сравнению с силой Fзат, растягивающей болт, в 1,3 раза
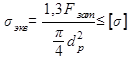 откуда
откуда 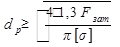 .
.
Расчет болтового соединения, нагруженного силами, сдвигающими
Деталь по стыку
Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах:
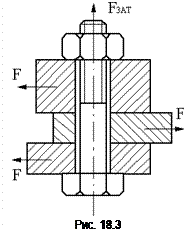 1. Болт поставлен с зазором. При этом внешнюю нагрузку F уравновешивают силами трения в стыке, которое образуется в стыке от затяжки болта (рис 18.3).
1. Болт поставлен с зазором. При этом внешнюю нагрузку F уравновешивают силами трения в стыке, которое образуется в стыке от затяжки болта (рис 18.3).
Условие равновесия
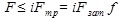 или
или 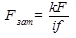 ,
,
где i – число плоскостей стыка деталей;
f– коэффициент трения; Fтр– сила трения; k – коэффициент запаса:
k=1,2¸1,5 - при статической нагрузке;
k=1,8¸2при переменной нагрузке.
Прочность болта оценивают по эквивалентному напряжению (см. выше).
В болтовом соединении с зазором внешняя нагрузка не передается на болт, поэтому болт рассчитывают только на статическую прочность по силе затяжки даже при переменной нагрузке.
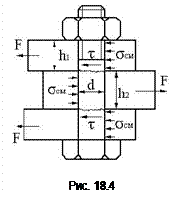 2. Болт поставлен без зазора (рис 18.4).
2. Болт поставлен без зазора (рис 18.4).
В этом случае отверстие калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим посадку типа напряженной (H7/k6).
При расчете прочности соединения не учитывают силы трения в стыке, т.к. затяжка болта необязательна. Стержень болта рассчитывают по напряжениям среза и смятия. Условие прочности по напряжениям среза
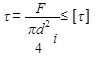 ,
,
где i – число плоскостей среза.
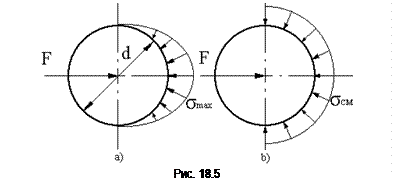 |

 Закон распределения напряжений смятия по цилиндрической поверхности контакта трудно установить точно. В значительной степени это зависит от величины натяга посадки, а также от точности цилиндрической формы стержня и отверстия. Поэтому расчет на смятие производят по условным напряжениям. Эпюру действительного распределения напряжений (рис. 18.5,а) заменяют условной (рис. 18.5,б) с равномерным распределением напряжений.
Закон распределения напряжений смятия по цилиндрической поверхности контакта трудно установить точно. В значительной степени это зависит от величины натяга посадки, а также от точности цилиндрической формы стержня и отверстия. Поэтому расчет на смятие производят по условным напряжениям. Эпюру действительного распределения напряжений (рис. 18.5,а) заменяют условной (рис. 18.5,б) с равномерным распределением напряжений. Условие прочности по напряжениям смятия
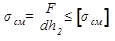 - для средней детали;
- для средней детали;
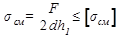 - для крайней детали.
- для крайней детали.
Эти формулы справедливы как для болта, так и для деталей.
Из двух значений sсм, в этих формулах расчет прочности выполняют по наибольшему, а допускаемое напряжение определяют по более слабому материалу болта или детали. Сравнивая варианты установки болтов с зазором или без зазора, следует отметить, что первый вариант дешевле второго, т.к. он не требует точных размеров болта и отверстия. Однако условия работы болта, поставленного с зазором, хуже, чем без зазора. Так, например, приняв коэффициент трения в стыке деталей f=0,2, k=1,5, i=1 для болта с зазором получим Fзат=7,5F. Иначе говоря, расчетная нагрузка болта с зазором в 7,5 раз превышает внешнюю нагрузку. Кроме того, вследствие нестабильности коэффициента трения и трудности контроля затяжки рабо-та таких соединений при сдвигающей нагрузке недостаточно надежна.
