Расчет закрытой зубчатой передачи

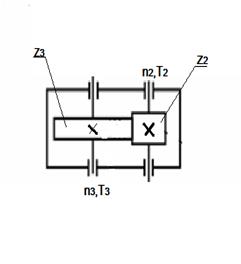
Рисунок 3- Схема закрытой зубчатой передачи

Исходные данные принимаются по результатам предыдущих расчетов:

- номинальный вращающий момент на ведомом валу проектируемой цилиндрической передачи: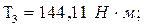

- номинальная частота вращения ведущего вала передачи

- передаточное отношение цилиндрической передачи

- коэффициент пиковой нагрузки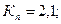

- допускаемые контактные напряжения при переменном режиме нагружения: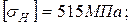

- допускаемые напряжения изгиба при переменном режиме нагружения шестерни и колеса: 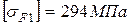и

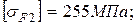
- допускаемые максимальные контактные напряжения: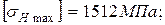

- допускаемые максимальные напряжения изгиба:

- коэффициенты долговечност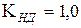и: и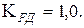

Рисунок 4 – Геометрические параметры цилиндрической

зубчатой передачи

Рисунок 5 – Схема сил в зацеплении цилиндрических прямозубых

зубчатых колёс

Расчет межосевого расстояния передачи и ширины зубчатых колес.

Предварительное значение межосевого расстояния из условия контактной выносливости рабочих поверхностей зубьев рассчитываем по формуле:

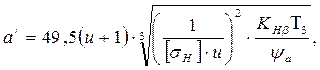(5.1)

где T₃ – вращающий момент на валу колеса

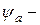коэффициент ширины колеса, который выбирают по таблице 2. 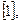при симметричном расположении относительно опор: .

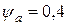Тогда предварительное межосевое расстояние примет значение:

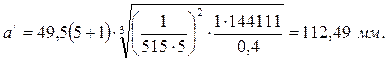
Рассчитанную величину округляем до ближайшего значения по единому ряду, т.е. принимаем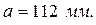

Предварительная ширина зубчатых колес и шестерни соответствует произведению:

Полученные расчетные значения округляем по единому ряду главных параметров редуктора: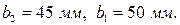

При твердости зубьев НВ 350 нормальный модуль зацепления выбирают из стандартного ряда в рекомендованном интервале:

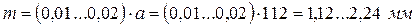. (5.4)

Принимаем нормальный модуль зацепления прямозубой цилиндрической передачи .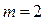

Предварительное суммарное число зубьев для прямозубых цилиндрических колес вычисляют по отношению:

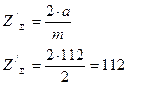
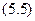
Предварительное значение числа зубьев шестерни находят из отношения:

Принимаем: .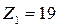

Число зубьев колеса:

Фактическое передаточное число соответствует:

Отклонение фактического передаточного числа составляет

Условия прочности по контактным напряжениям при переменном режиме нагружении имеет вид

где K_HV2 – коэффициент динамичности нагрузки зубьев колеса при контактных напряжениях. Он зависит от окружной скорости вращения колес 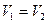, рассчитываемой по зависимости

Этой скорости соответствует 9-я степень точности .

Тогда при скорости 1,37 м/с, 9-й степени точности и твердости зубьев 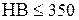выбираем .

Т а б л и ц а 3 – Значения К_HV2 – коэффициента динамичности нагрузки при контактных напряжениях

Степень точности	Окружная скорость V, м/с
	–	–	–	1,21	1,29	1,36
	–	1,08	1,16	1,24	–	–
	1,05	1,1	–	–	–	–

Действительное контактное напряжение равно

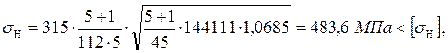
т.е. условие поверхностной прочности зубьев при переменном режиме нагружения выполняется.

Разница между расчетными и допускаемыми напряжениями определяют по зависимости

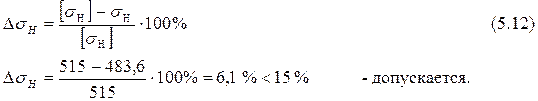
Расчетное максимальное напряжение при кратковременных перегрузках имеет вид

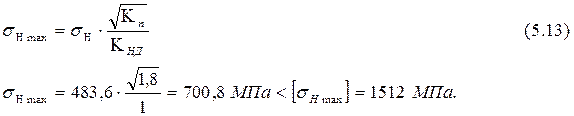
Поскольку расчетное максимальное напряжение меньше допускаемого, то условие статической контактной прочности при кратковременных перегрузках выполняется.

Расчет закрытой цилиндрической прямозубой передачи проведен только по контактным напряжениям, так как большая статистика расчетов этих передач при средних режимах нагружения и длительном режиме эксплуатации показывает, что при обеспечении контактной прочности изгибная прочность выполняется.