Основы динамического расчета двигателя
3.1. Силы, действующие в КШМ при заданном угле поворота кривошипа φ
Кривошипно-шатунный механизм при работе двигателя нагружают два вида сил: силы от давления газов в цилиндре и силы инерции (рис. 2).
|
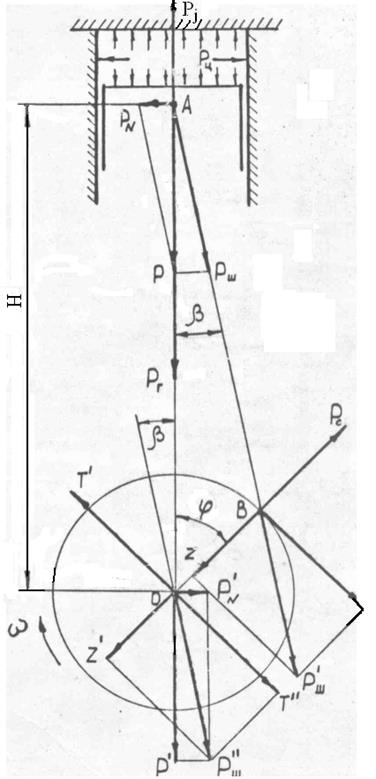
Рис.2 Схема разложения сил в кривошипно-шатунном механизме
Сила от давления газов на поршень Рг всегда направлена по оси цилиндра и её принимают приложенной к центру поршневого пальца. Зная величину давления газов в цилиндре, можно определить эту силу по выражению
Рr = (рц - ро) Fп ·106, Н (3.1)
где рц - текущее значение давления газов в цилиндре, взятое по индикаторной диаграмме, МПа;
ро - давление газов в картере, условно принятое равным давлению окружающей среды, ро = 0,1 МПа;
Fп - площадь поршня, м2 (Fп = p·D2 /4);
D - диаметр цилиндра, м.
Для определения рц при различных углах поворота кривошипа коленвала необходимо под индикаторной диаграммой построить полуокружность с диаметром, равным ходу поршня S (рис.1). Затем от ее центра точки О отложить в сторону НМТ поправку Ф.Брикса 00¢, рассчитанную по формуле
00¢ = R· lк /2, м
где R = S/2 - радиус кривошипа, м;
lк = R/L- конструктивный параметр КШМ;
L - длина шатуна, м;
и разделить полуокружность на части через 30о п.к.в.
Физический смысл поправки Ф.Брикса заключается в том, что она учитывает несколько большие перемещения поршня при повороте кривошипа от 0 до 90о п.к.в., при котором поршень проходит больше половины своего полного хода S = R(1+lк /2) по сравнению с перемещением при повороте от 90 до 180о п.к.в.
Из полученного центра 0¢ проводят лучи через 30опараллельно первым. Из полученных новых точек проводят вертикально вверх лучи до пересечения с линиями индикаторной диаграммы. Проекции полученных точек на ось давления будут соответствовать искомому давлению газов в цилиндре при соответствующих углах поворота кривошипа, которые заносят в таблицу3.1.
Силы инерции подразделяются на силы инерции от возвратно-поступательно движущихся масс и силы от вращающихся масс.
Данные силы инерции создают вибрацию двигателя в плоскости оси цилиндра и плоскости кривошипа. В многоцилиндровых двигателях эти силы образуют моменты, также вызывающие вибрацию двигателя. Для снижения вибрации в КШМ большинства двигателей устанавливаются механизмы для уравновешивания сил инерции первого и второго порядков, центробежных сил, а также моментов этих сил. Уравновешивающие механизмы конструктивно выполняют в виде противовесов, устанавливаемых на коленчатом валу или на дополнительных валах.
Сила инерции возвратно-поступательно движущихся масс всегда направлена по оси цилиндра противоположно Рг и приложена в центре поршневого пальца. Ее определяют по выражению:
Рj = - m·j = - mj R w2 (cosj + lк cos2j), Н (3.2)
где mj - масса возвратно-движущихся частей КШМ, приведенная к центру пальца,кг;
j - ускорение поршня
mj = mпк + 0,275 mш ,
где mпк - масса поршневого комплекта в сборе, кг (см. прилож.1);
mш - масса шатуна, кг (табл.);
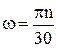 - угловая частота вращения коленчатого вала, рад/с, где n - частота вращения коленчатого вала, об/мин.
- угловая частота вращения коленчатого вала, рад/с, где n - частота вращения коленчатого вала, об/мин.
Для упрощения расчетов Рj считают по формуле:
Рj = mj R w2А, Н
где А - приведена в приложении 2.
Суммарная сила, действующая на поршень по оси цилиндра, считается приложенной к оси поршневого пальца и определяется алгебраическим сложением силы давления газа и силы инерции возвратно-поступательно движущихся масс
P = Рг + (± Рj), Н (3.3)
Разложив по правилу параллелограмма эту силу на две составляющие по оси шатуна Рш и нормали N к стенке цилиндра получим:
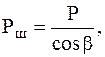 Н (3.4)
Н (3.4)
N = P · tgb, Н (3.5)
Первая сила Рш будет нагружать шатун и передаваться на шатунную шейку коленвала, а вторая N прижимать поршень к стенке цилиндра, вызывая износ и повышенные потери на трение.
От действия силы Рш через шатун на шатунную шейку коленчатого вала возникают радиальная сила Z, действующая по радиусу кривошипа:
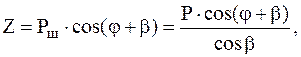 Н (3.6)
Н (3.6)
и тангенциальная сила Т, направленная перпендикулярно радиусу окружности R:
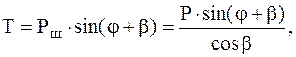 Н (3.7)
Н (3.7)
Если радиальную силу Z перенести в центр О (Z¢) коренной шейки и приложить две взаимно уравновешенные силы Т¢ и Т², параллельные и равные силе Т, то в результате получим пару сил Т и Т¢, которые приводят во вращение коленчатый вал. Момент этой пары сил называют крутящим моментом (Мк.ц) двигателя одного цилиндра:
Мк.ц = Т · R, Н·м (3.8)
Если сложить оставшиеся силы Т΄΄ и Ζ΄, то получим равнодействующую рш΄΄, равную силе рш, которую можно разложить на составляющие р΄Ν и р΄.
Силы р΄Ν и р Ν образуют пару сил, момент которой называется опрокидывающим моментом Мопр.;
Мопр.= ΝН, Н∙м. (3.9)
Максимальное значение силы Т наблюдается при j = 390...4000. Для карбюраторных двигателей Тmax = 0,4рz , а для дизелей Тmax = 0,6рz.
Максимальное значение силы инерции рj определяется из формулы (3.2) при j = 0, то есть когда поршень находится в ВМТ в конце такта сжатия или выпуска.
Максимальное значение сил давления газов обычно принимается для положения поршня (8…15 п.к.в.) после ВМТ.
Равнодействующая от сил инерции вращающихся масс направлена по радиусу кривошипа и приложена к центру шатунной шейки:
Pс = - mв · R · w2, Н
где mв - масса вращающихся частей КШМ, кг;
mв = mшк + mк ,
mшк = 0,725 mш, масса шатуна , отнесенная к кривошипной головке
(приводится в таблице);
mк - неуравновешенная масса кривошипа, которую можно определить по эмпирическим зависимостям: mк = (150...200)·F п - для бензиновых ДВС с диаметром центра Dц = 60-100 мм; mк = (200...400)·F п - для дизелей c
Dц = 80-120 мм; F п - площадь поршня, F п = p · D2/4, м2.
Определение всех сил при заданном положении кривошипа наиболее просто проводится графо-аналитическим методом:
а) начертить в масштабе схему КШМ (Мкшм 1:1; 1:2 или др.) при заданном положении кривошипа j (по заданию);
б) определить силы Рг , Рj и Рс при заданном положении кривошипа и нанести векторы этих сил на схему КШМ в выбранном масштабе на схему КШМ;
в) графически разложить векторы сил, действующих в КШМ согласно рис.;
г) по построенным векторам определить графически силы Рс, N, Рш, Т, Z;
д) рассчитать силы Рс, N, Рш, Т, Z по формулам и сравнить затем их аналитические и графические значения.