Расчет на сопротивление усталости

Условие прочности

,

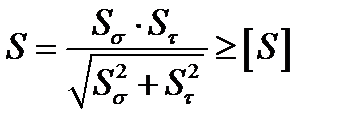где S, [S] – расчетный и допускаемый коэффициенты запаса прочности,

[S] = 1,5…4

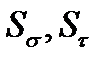- коэффициенты запаса прочности при изгибе и кручении;

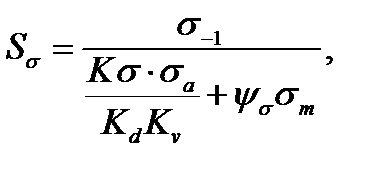
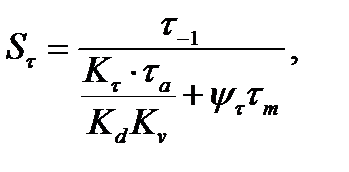
здесь 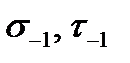- предел выносливости материала вала при изгибе и кручении;

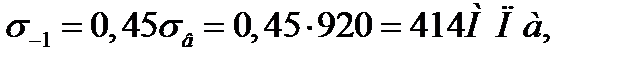
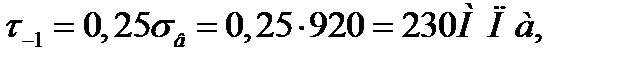
здесь 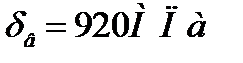- предел прочности материала вала;

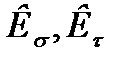- эффективные коэффициенты концентрации нагрузки;

k_σ = k_σф +k_σn -1,

k_τ = k_τф +k_τn -1,

здесь k_σф, k_τф – эффективные коэффициенты от формы;

k_σф = 1, k_τф = 1 [7, с 271]

k_σn, k_τn – эффективные коэффициенты от состояния поверхности;

k_σn = 1 k_τn = 1 [7, с 271]

k_σ = 1+1-1=1, k_τ = 1+1-1=1,

k_dσ, k_dτ – масштабный фактор;

k_dσ = 0,62 k_dτ = 0,62 [7, с 272]

k_ν – коэффициент поверхностного упрочнения;

k_ν = 1 – для улучшения;

ψ_σ, ψ_τ – коэффициенты чувствительности с ассиметрии цикла;

ψ_σ =0,1;ψ_τ = 0,05 ,

σ_a, τ_a – амплитуды напряжения;

σ_m, τ_m – среднее значение;

Условимся, что напряжение изгиба изменяется по амплитудному циклу, а напряжение кручения по отнулевому.

σ_a = σ_u = 0,617 Нм;

σ_m = 0;

τ_a = τ_m = τ_кр/2 = 0,537/2 = 0,269 Нм,

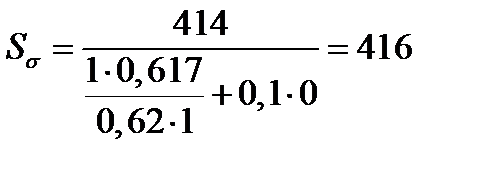
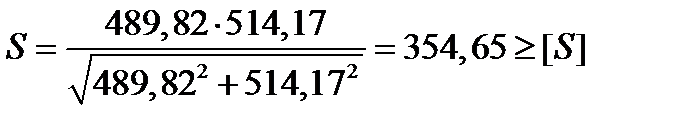
Промежуточный вал редуктора.

Материал вала: 40Х, термообработка улучшение.

σ_в = 92 0МПа, σ_т = 750 МПа;

Проверяемое сечение 6-6 (под колесом), 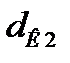= 40 мм.

Концентрация напряжений обусловлена наличием шпоночной канавки на валу.

Расчет на статическую прочность.

Условие прочности

,

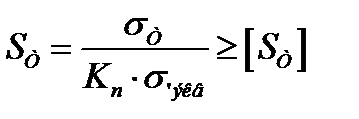где 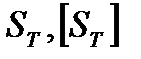- расчетный и допускаемый коэффициент запаса прочности по текучести,

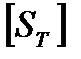= 1,2…1,8,

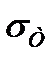- предел текучести,

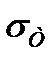= 750 МПа

- коэффициент перегрузки;

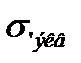- эквивалентное напряжение,

,

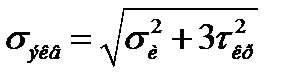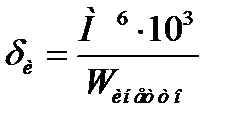здесь 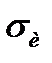- напряжение изгиба в проверяемом сечении;

здесь 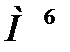- суммарный изгибающий момент в проверяемом сечении,

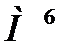= 187,4 Нм

- момент сопротивления сечения изгибу,

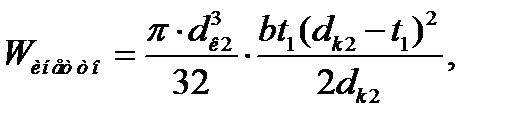
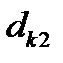=40 – диаметр вала под колесом;

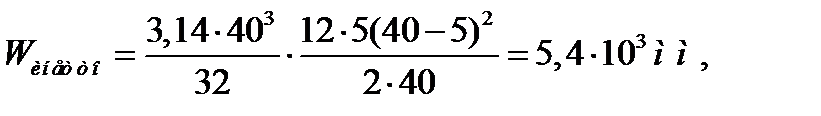
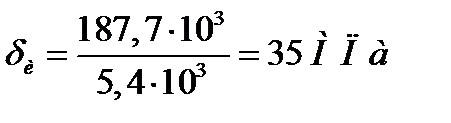
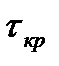- напряжение кручения в проверяемом сечение,

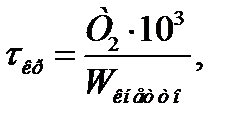
здесь 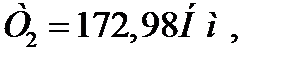-передаваемый валом вращающийся момент;

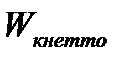- момент сопротивления сечения вала кручению.

,

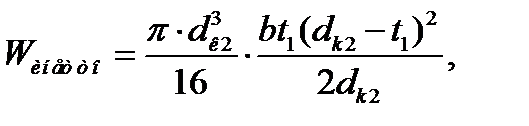
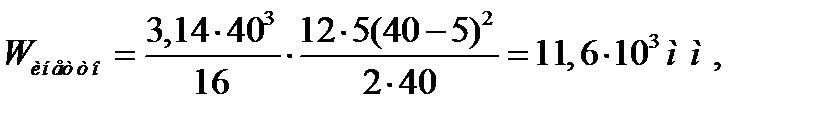
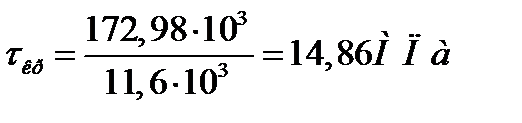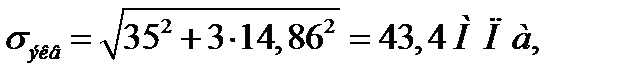
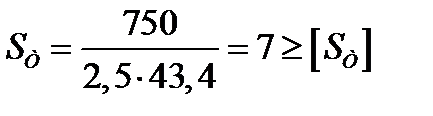
Расчет на сопротивление усталости.

Условие прочности

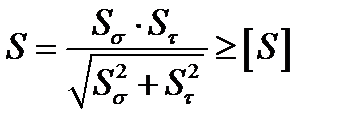
где S, [S] – расчетный и допускаемый коэффициенты запаса прочности,

[S] = 1,5…4

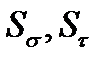- коэффициенты запаса прочности при изгибе и кручении;

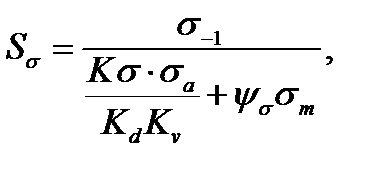
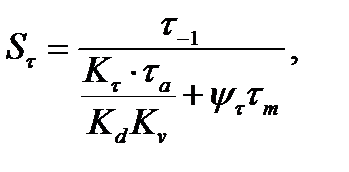
десь 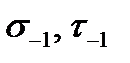- предел выносливости материала вала при изгибе и кручении;

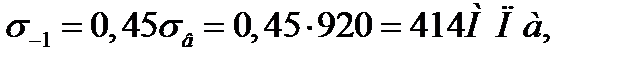
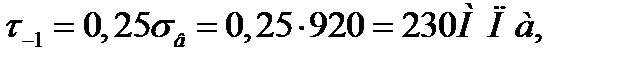
здесь 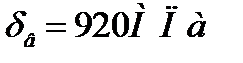- предел прочности материала вала;

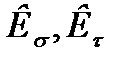- эффективные коэффициенты концентрации нагрузки;

k_σ = k_σф +k_σn -1,

k_τ = k_τф +k_τn -1,

здесь k_σф, k_τф – эффективные коэффициенты от формы;

k_σф = 2, k_τф = 1,7 [7, с 272]

k_σn, k_τn – эффективные коэффициенты от состояния поверхности;

k_σn = 1 k_τn = 1 [7, с 272]

k_σ = 2+1-1=2, k_τ = 1,7+1-1=1,7;

k_dσ, k_dτ – масштабный фактор;

k_dσ = 0,73 k_dτ = 0,73 [7, с 272]

k_ν – коэффициент поверхностного упрочнения;

k_ν = 1 – для улучшения;

ψ_σ, ψ_τ – коэффициенты чувствительности с ассиметрии цикла;

ψ_σ =0,1;ψ_τ = 0,05 ,

σ_a, τ_a – амплитуды напряжения;

σ_m, τ_m – среднее значение;

Условимся, что напряжение изгиба изменяется по амплитудному циклу, а напряжение кручения по отнулевому.

σ_a = σ_u = 35 МПа;

σ_m = 0;

τ_a = τ_m = τ_кр/2 = 14,86/2 = 7,4 МПа,

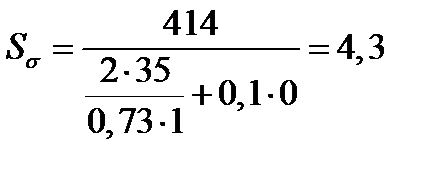
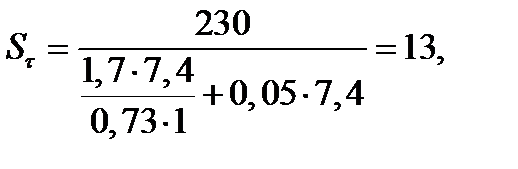
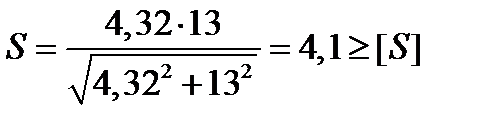
Ведомый вал.

Материал вала - сталь 45, термообработка - улучшение,

σ_в = 780МПа, σ_т = 540 МПа; Проверяемое сечение 7-7 ( под колесом), d_к3= 60 мм.

Концентрация напряжений обусловлена наличием шпоночной канавки на валу.