Расчёт закрытой цилиндрической зубчатой передачи
4.1 Проектный расчёт.
4.1.1. Определяю главный параметр – межосевое расстояние аw,мм:
аw = Ка ( U+1 )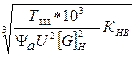 
где Ка – вспомогательный коэффициент. Для шевронных передач Ка = 43 (стр. 58 [1]);
Ψа – коэффициент ширины венца колеса, равный 0,28…0,36 (стр.58[1]) – для шестерни, расположенной симметрично относительно опор в проектируемых нестандартных одноступенчатых редукторах;
U – передаточное число редуктора;
ТIII – вращающий момент на тихоходном валу редуктора или на приводном валу рабочей машины для открытой передачи, Нм;
[G]н – допускаемое контактное напряжение колеса с менее прочным зубом или среднее допускаемое контактное напряжение, Н/мм².
Kнв – коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев Kнв = 1(табл. 3.1, стр. 49 [1]).
аw = 43 (4+1)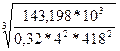 
= 215* 
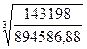= 215*0,542 = 116,53 мм.
Полученное межосевое расстояние округлить до ближайшего значения из ряда нормальных линейных размеров (табл. 13.15, стр. 313 [1]).
аw = 116 мм.
4.1.2 Определяю модуль зацепления М, мм:
М≥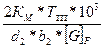 
Км - для косозубых передач равен 5,8 (стр. 59 [1]).
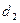= 2 аw * U / (U + 1) = 2*116*4 / 5 = 185,6
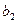= Ψа * аw = 0,32 * 116 = 37,12
М ≥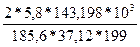 
= 
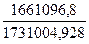=1,2 мм.
Если модуль получили меньше 2 мм, то, несмотря на полученное значение, принимаем за 2 мм., т.к в силовых передачах значение модуля меньше 2 мм. не рекомендуется из-за опасности большого понижения несущей способности в результате износа, повышенного влияния неоднородности материала, опасности разрушения при перегородках ( уч. Решетов «Детали машин», стр. 266).
М = 2 мм.
4.1.3 Определяю угол наклона зубьев βmin:
βmin = arcsin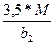 
= arcsin 
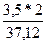= arcsin 0,187 = 10°
Полученное значение удовлетворяет условию 8…16°.
4.1.4 Определяю суммарное число зубьев шестерни и колеса:
Z∑ = Z1 + Z2 = 2 аw * cos βmin / M = 2*116*0,985 / 2 = 114,26
Полученное значение Z∑ округляем в меньшую сторону до целого числа.
Z∑ = 114
4.1.5 Уточняем действительную величину угла наклона зубьев для шевронных передач:
β = arccos Z∑ М / (2 аw) = arcos 114*2 / 2*116 = arcos 0,983 = 10° 57984’ 
4.1.6 Определяю число зубьев шестерни:
Z1 = Z∑ / (1+U) = 114 / 5 = 22,8
Значение Z1 округляю до ближайшего целого числа: Z1 = 23
4.1.7 Определяю число зубьев колеса:
Z2 = Z∑ - Z1 = 114 – 23 = 91
4.1.8 Определяю фактическое передаточное число Uф и проверяю его отклонение ∆U от заданного U:
Uф = Z2 / Z1 = 91 / 23 = 3,956;
∆U =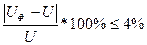 
(стр. 60 [1]).
∆U =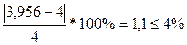 
Полученное значение отклонения удовлетворяет условию:
∆U ≤ 4%
4.1.9 Определяю фактическое межосевое расстояние:
аw = (Z1 + Z2) * М / (2cosβ) = (23+91) *2 / (2*cos10) =228 / 1,969=115,8 мм.
4.1.10 Определяем основные геометрические параметры передачи:
d1 = M* Z1 / cosβ = 2*23 / 0,984 = 46,747 мм.
d2 = M*Z2 / cosβ= 2*91 / 0,984 = 184,959 мм.
dа1 = d1+2М = 46,747+2*2 = 50,747 мм.
dа2 = d2+2М = 184,959+2*2 = 188,954 мм.
df1 = d1 - 2,4М = 46,747 - 4,8 = 41,947 мм.
df2 = d2 - 2,4М = 184,959 - 4,8 = 180,159 мм.
b2 = Ψа * аw = 0,32 * 116 = 37,12 мм.
У шевронных передач b1 = b2: b1 = 37,12 мм. Точность вычисления делительных диаметров колес до 0,1 мм., значение ширины зубчатых венцов округляем до целого числа по нормальным линейным размерам (табл. 13.15, стр. 313 [1]).
Составляем табличный ответ:
| Параметр, мм. | Шестерня | Колесо |
| Делительный диаметр, d | ||
| Диаметр вершин зубьев, dа | ||
| Диаметр впадин зубьев, df | ||
| Ширина венца, b |
4.2 Проверочный расчет:
4.2.1 Проверяем межосевое расстояние:
аw = (d1 + d2) / 2 = (46,747+184,959) / 2 = 115,853 мм.
4.2.2 Проверяем пригодность заготовок колес:
Условие пригодности заготовок колес:
Dзаг ≤ Dпред.; Сзаг (Sзаг) ≤ Sпред.
Dзаг1 = dа1+ 6 мм. = 50,747+6 = 56,747 мм., т.к Dпред = 125 мм. выполняется условие: 56,747≤125, заготовка пригодна.
Sзаг2 = b2+4 мм. = 37,12+4 = 41,12 мм., т.к. Sпред. = 80 мм. выполняется условие: 41,12≤80, заготовка пригодна.
4.2.3 Проверяю контактные напряжения Gн, Н/мм²:
Gн = К*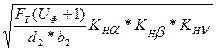 
≤ [Gн]
где К – вспомогательный коэффициент. Для шевронных передач К = 376 (стр. 61 [1]).
FT = 2 Т III * 10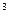 
/ d2 = 2*143198 / 185,231 = 1546,155 – окружная сила зацеплений, Н.
Кнα – коэффициент, учитывающий распределение нагрузки между зубьями. Для шевронных передач Кнα определяют по графику (рис. 4.2., стр. 63 [1]) в зависимости от окружной скорости колес V и степени точности передач.
V = WIII * d2 / 2*10 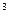= 12,563*184,959 / 2000 = 1,161 м/с.
Степень точности передачи – 9 (табл. 4.2., стр. 62 [1])
Кнα = 1,12.
Кнβ = 1 (стр. 59 [1]) – коэффициент неравномерности нагрузки по длине зуба.
Кнν – коэффициент динамической нагрузки, зависящий от окружной скорости колес V и степени точности передач. Кнν = 1,01(табл. 4.3., стр. 62 [1])
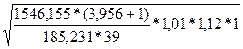Gн =376 
=376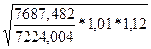 
=412 Н/мм²
В данном случае [Gн] = 418 Н/мм². Наблюдается недогрузка передачи на 1,4%. Допускаемая недогрузка 10%, условие выполнено.
4.2.4 Проверяем напряжение изгиба зубьев шестерни GF1 и колеса GF2, Н/мм².
GF2 = YF2*Yβ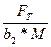 
* КFα* КFβ* КFV≤ [G]F2
GF1 = GF2 * YF1 / YF2 ≤ [G]F1
где М – модуль зацепления, мм.
b2 – ширина зубчатого венца колеса, мм.
FT – окружная сила зацеплений, Н.
КFα – коэффициент, учитывающий распределение нагрузки между зубьями, для шевронных передач КFα =1(стр. 63 [1]).
КFβ –коэффициент неравномерности нагрузки по длине зуба. КFβ =1(стр. 63 [1]).
КFV – коэффициент динамической нагрузки. КFV = 1,01(табл. 4.3., стр. 62 [1]).
YF1 и YF2 – коэффициенты формы зуба шестерни и колеса. Определяются по таблице 4.4, стр. 64[1] в зависимости от эквивалентного числа зубьев шестерни Z1 , и колеса Z2.
ZV1 = Z1 / cosβ 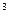= 23 / 0,952 =24,159; YF1 = 3,7
ZV2 = Z2 / cosβ² = 91 / 0,968 =94,008; YF2 = 3,62
Yβ = 1 - β /140 = 1 – 10 / 140 = 0,929 – коэффициент, учитывающий наклон зуба.
GF2 = 3,62*0,929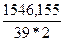 
*1,04 = 69,327 Н/мм²
GF1 = 69,327*3,7 / 3,62 = 70,859 Н/мм²
Если GF значительно меньше [G]F, то это допустимо, т.к. нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью. Условие выполнено.
4.2.5 Составляем табличный ответ:
Параметры зубчатой цилиндрической передачи, мм.
Проверочный расчет:
| Параметр | Допускаемые значения | Расчетные значения | Примечания |
| Контактные напряжения, Gн | 418 Н/мм² | 412 Н/мм² | -1,4% |
| Напряжения изгиба, GF1 | 256 Н/мм² | 70,859 Н/мм² | -72% |
| Напряжения изгиба, GF2 | 199 Н/мм² | 69,327 Н/мм² | -65% |
Проектный расчет: