Порядок выполнения работы и обработка опытных данных
1. При закрытом вентиле 5 открыть вентиль 9 для заполнения бака 1 и трубопровода 2 водой. При этом следует обратить внимание на уровни воды в пьезометрических 3 и скоростных трубках 4. Эти уровни при отсутствии воздуха в системе должны быть на одной отметке.
2. Открыть вентиль 5 так, чтобы трубопровод 2 работал полным сечением, а уровень воды в баке постоянным.
3. Измерить с помощью бака 6 и секундомера 7 расход воды. Затем линейкой измерить геометрические высоты z центров тяжести сечений I-I…II-II относительно плоскости сравнения 0-0, отмеченной на установке.
4. Далее, определить по шкалам отметки уровней воды в пьезометрах и скоростных трубках в сечениях I-I…II-II. Результаты всех измерений записать в таблицу 1.3. Затем выполнить все вычисления, предусмотренные табл. 1.3, и построить в масштабе по полученным данным линии полного напора и пьезометрическую, так, как показано на рис. 1.5.
5. Дать заключение по результатам работы.
Основные контрольные вопросы
1. Поясните геометрический смысл слагаемых уравнения Д. Бернулли.
2. Поясните энергетический смысл слагаемых уравнения Д. Бернулли.
3. Как называется коэффициент a, входящий в уравнение Д. Бернулли для потока реальной жидкости, что он учитывает и от чего зависит его величина?
4. Объясните, что обусловлены потери полного напора и каков их энергетический смысл?
5. Поясните, что понимают под термином "удельная энергия"?
6. Объясните термины "местная скорость" и "средняя скорость" и укажите, как определяют эти скорости?
7. Поясните, что такое скоростная трубка и трубка Пито?
8. Поясните, что такое линия полного напора и пьезометрическая линия, что будут представлять собой эти линии при равномерном движении реальной жидкости?
9. Что понимают под термином «живое сечение потока жидкости»?
Учебная литература к работе 1.2 :
1.(с. 85…94, 97…114); 2.(с. 68…75); 3.(с.37…42); 4.(с. 61…64, с. 68…67);5.(с.84…88,с.28…104).
Таблица 1.3
| № поз. | Наименования и обозначения измеряемых и вычисляемых величин | Ед. Изм. | Результаты измерений и вычислений | ||
| I-I | II-II | III-III | |||
| Геометрические высоты центров тяжести сечений z Отметки уровней воды в пьезометрах, т.е. гидростатические напоры (z+p/rg) Отметки уровней воды в скоростных трубках, т.е. полные напоры H=z + P/rg + U2/2g Пьезометрические высоты (z + P/rg ) –z Скоростные высоты U2/2g=H-(z + P/rg) Потери полного напора на пути между соседними живыми сечениями струйками h`wi-(i+1)=Hi – Hi+1 Суммарные потери полного напора h`wI-III=HI - HIII Объем воды в мерном баке W Продолжительность наполнения объема W в мерном баке t Расход воды в трубопроводе Q=W/t Средняя скорость движения воды в V= Q/w Скоростная высота, отвечающая средней скорости V2/2g Разность скоростных высот (U2/2g – V2/2g) | м м м м м м м м3 с м3/c м/с м м |
Примечание к табл. 1.3:
1. Для сечения III-III (см графу 6) числовые значения величин (см.
позиции 5 и 8…13) те же, что и для сечения II-II
2. Потери полного напора h`w (см. позицию 6) между сечениями II-II и III-III принять равными потерям напора между сечениями I-I и II-II
3. Остальные величины для сеч. III-III (см. позиции 1…4) следует определить с привлечением уравнения Д. Бернулли (см. уравнение 1.11)
Работа 1.3.ЭКСПЕРИМЕНТАЛЬНАЯ ИЛЛЮСТРАЦИЯ ЛАМИНАРНОГО И ТУРБУЛЕНТНОГО РЕЖИМОВ ДВИЖЕНИЯ ЖИДКОСТИ, ОПРЕДЕЛЕНИЕ ЗАКОНОВ СОПРОТИВЛЕНИЯ И КРИТИЧЕСКОГО ЧИСЛА РЕЙНОЛЬДСА.
Вводная часть. Многочисленными экспериментальными исследованиями установлено, что движение жидкости может происходить или при ламинарном, или при турбулентном режиме.
Ламинарный режим наблюдается при небольших скоростях движения. При этом окрашенные струйки жидкости не перемешиваются, сохраняясь по всей длине потока, т.е. движение жидкости при ламинарном режиме является струйчатым, перемешивание частиц жидкости отсутствует.
Турбулентный режим наблюдается при значительных скоростях и характеризуется интенсивным перемешиванием частиц жидкости, что обуславливает пульсацию скоростей и давления,
Средняя скорость потока, при которой происходит смена режима движения жидкости, называется критической (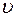 
кр). Величина ее, как показывают опыты в трубопроводах круглого сечения, зависит от рода жидкости, характеризуемого динамической вязкостью m, и плотностью, а также от диаметра трубопровода d. Одновременно опытами установлено, что величина безразмерного алгебраического комплекса, отвечающей критической скорости 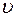кр,
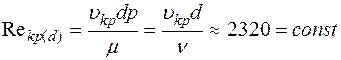(1.13)
от m, r и d не зависит. Reкр(d)=2320 называется критическим числом Рейнольдса. Устойчивый ламинарный режим наблюдается при значениях числа Рейнольдса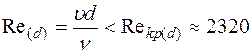 
, а турбулентный – при
Re(d)>Reкр(d).
Таким образом, число Рейнольдса
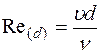(1.14)
является критерием, позволяющим судить о режиме движения жидкости в круглой трубе, работающей полным сечением.
Величину u=m/r, входящую в формулу (1.13) и (1.14), называют кинематическим коэффициентом вязкости жидкости.
Из изложенного следует, что для определения режима движения жидкости в круглом трубопроводе при напорном движении достаточно вычислить по формуле (1.14) число Рейнольдса и сравнить его с критическим.
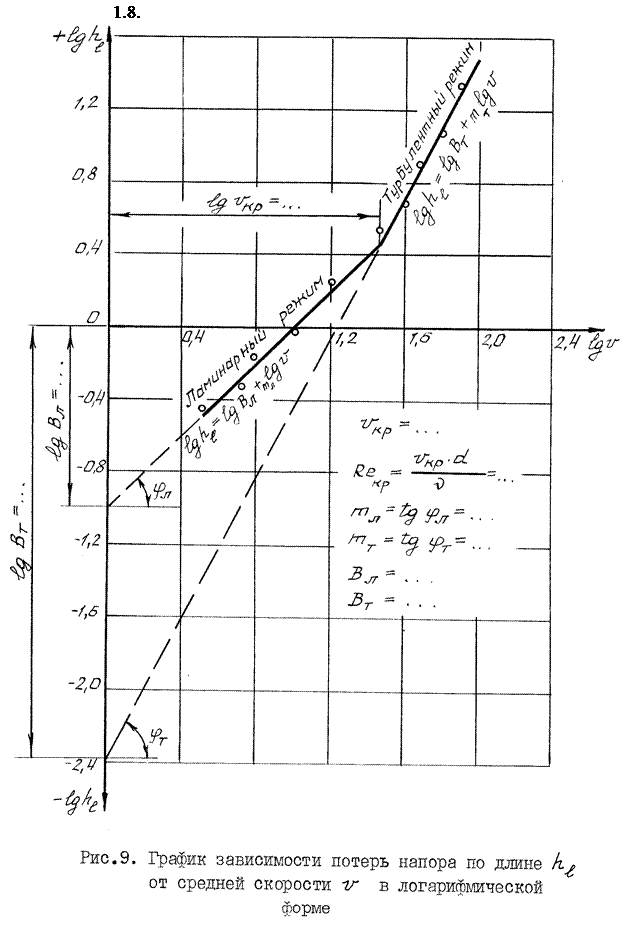
Знание режима, движения жидкости необходимо для правильной оценки потерь напора при гидравлических расчетах. Дело в том, что, как показывают опыты в круглых трубах при напорном равномерном движении (результаты их представлены на рис. 1.8 в виде графика зависимости потерь напора по длине he от средней скорости )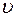
При ламинарном режиме потери напора he пропорциональны средней скорости 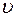в первой степени, а при турбулентном - в степени 1,75 <m>2,0. Заметим, что с помощью этого графика определяют величину критической скорости 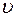кр, а через нее - и критическое число Рейнольдса по формуле (1.13).
Цель работы.1. Убедиться на опыте путем окрашивания струйки воды в стеклянной трубе в существовании ламинарного и турбулентного режимов.
2. Вычислить по данным опытов, проведенных на этой трубе, числа Рейнольдса при ламинарном и турбулентною режимах, сравнить их с критическим, убедиться, что при ламинарном режиме Rе< Reкр , а при турбулентном – Re > Reкр.
3. Построить по опытным данным, полученным на винипластовой трубе, график lghe=f(lg 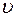), определить с его помощью критическую скорость 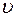кр, а через нее вычислить критическое число Reкр=2320.
4. Подтвердить с помощью графика lghe=f(lg 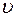), что при ламинарном режиме потери напора по длине he пропорциональны средней скорости в первой степени, а при турбулентном - в степени 1,75 £ m £ 2.
Описание установки (рис 1.9) включает в себя две расположенные горизонтально трубы: стеклянную 1 (d=1,6 cм) и винипластовую 2 (d=0,9 см), в которых и изучается движение воды при различных режимах, напорный бак 3, емкость 11 с раствором красителя, подаваемого открытием краника 10 по трубке 9 во входное сечение трубы 1. Для измерения расхода воды в трубах 1 и 2 служат мерная емкость 16 и секундомер 15.
Вода в напорный бак 3 подается по питающему трубопроводу 4 открытием вентиля 5 из резервуара лаборатории. Для поддержания уровня воды в баке 3 во время опытов на постоянной отметке имеется переливное устройство 6, для контроля за уровнем воды служит электрический уровнемер 7 со световой сигнализацией.
Температура воды в баке 3 измеряется термометром 8.
Регулирование расхода воды, а следовательно и средней скорости ее движения в трубах 1 и 2, осуществляется кранами соответственно 14 и 13. На винипластовой трубе 2 имеются пьезометры 12 для определения потерь напора по длине he (по разности их показаний).