Основы теории расчета ременных передач. Силы и напряжения в ремнях, кривые скольжения и допускаемые полезные напряжения

6.24. Силы натяжения в ветвях ремня (F_o, F_x, F₂).

Для создания необходимого трения между ремнем и ободом шкива ре­мень должен иметь достаточную силу начального натяжения F_o. Это дости­гается предварительным натяжением ремня при монтаже или с помощью подвижной опоры. Чем больше F_o, тем выше тяговая способность переда­чи. Но при большом начальном натяжении ремень получает и большую вытяжку, снижается его долговечность. Поэтому F_o выбирают таким, чтобы ремень мог сохранить это натяжение достаточно длительное время, не по­лучая большой вытяжки. Начальную силу натяжения ремня определяют по формуле

F_o = Аσ₀, (6.16)

где А — площадь поперечного сечения ремня; с₀ — начальное напряжение в ремне (см. шаг 6.27).

Приближенно можно считать, что в состоянии покоя и при холостом ходе каждая ветвь натянута одним и тем же усилием F_o (рис. 6.12, а)

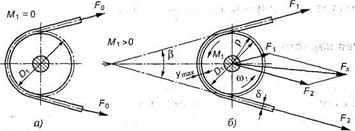Рис. 6.12. Усилия в ветвях ремня: а — на холостом ходу; б — при передаче нагрузки

С приложением момента T₁ ведущая ветвь натягивается до значения F₁, на­тяжение ведомой ветви уменьшается до F₂ (рис. 6.12, б). Силы натяжения F, и F₂, можно определить из условия равновесия шкива

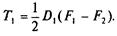(6.17)

Отсюда

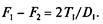(6.18)

С учетом того, что окружная сила на шкиве

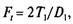(6.19)

получим

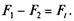(6.20)

Так как сумма сил натяжения ветвей ремпя постоянна (независимо от того, нагружена передача или нет), то

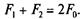(6.21)

Из равенств (6.20) и (6.21) следует, что

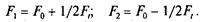(6.22)

Как называются силы Fо; F₁; Fi; F, (см. рис. 6.12)?

6.25.При обегании ремнем шкивов возникают центробежные силы F_v, которые отбрасывают ремень от шкива:

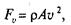
(6.23)

где р — плотность материала ремня, кг/м³; А — площадь сечения ремня, м²; и — окружная скорость, м/с.

С учетом центробежной силы натяжения определяют по следующим формулам для холостого хода:

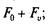(6.24)

для ведущей ветви

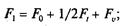(6.25)

для ведомой ветви

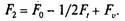. (6.26)

От каких параметров ременной передачи зависит центробежная сила F_v?

6.26.Нагрузка на валы и опоры F_s.

Силы натяжения ветвей ремня Р_{ и F₂, (за исключением силы F_v) пере­даются на валы и опоры. Рассматривая параллелограмм сил (см. рис. 6.12, б), находят равнодействующую сил

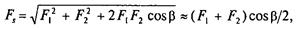(6.27)

где р — угол между ветвями ремня.

Поставим в выражение (6.21) вместо (i*¹, + F₂) величину 2F₀ [см. форму­лу (6.25)]; получим

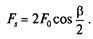(6.28)

Выражение (6.28) можно преобразовать через окружную силу F_r В этом случае можно считать, что для прорезиненных и кожаных ремней F_s« 2,5/); для хлопчатобумажных F_s» 3/); для шерстяных /)» 4/). Таким образом, на­грузка на валы в 2,5—4 раза превышает окружную силу F_t, что является не­достатком ременных передач.

6.27.Напряжения в ремне. При работе ременной передачи напряжения в различных сечениях по длине ремня неодинаковы. Изобразим эти напря­жения отрезками соответствующей длины, проведя их перпендикулярно поверхности ремня. Получим эпюру суммарных напряжений (рис. 6.13).

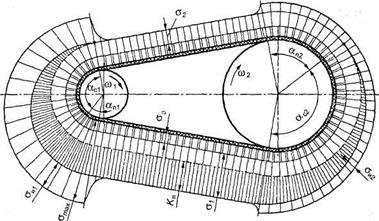
Рис. 6.13. Напряжения в поперечных сечениях ремня

Различают следующие виды напряжений в ремне.

1. Предварительное напряжение о₀, определяемое в зависимости от силы начального натяжения:

σ₀=F₀/A, (6.29)

где А — площадь поперечного сечения ремня.

Для стандартных ремней рекомендуется принимать: и_о= 1,76 МПа — для плоских ремней; ..

ст₀ = 1,18 -г 1,47 МПа — для клиновых.

2. Удельная окружная сила (полезное напряжение) К_п. Это напряжение зависит от передаваемой ремнем окружной силы F;.

K_n=F_t/A. (6.30)

Полезное напряжений можно определить и как разность напряжений σ₁ и σ₂:

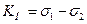(6.31)

где σ₁ и σ₂— напряжения в ведущей и ведомой ветвях.

По значению К_П оценивается тяговая способность ременной передачи.

3. Напряжение изгиба о_и, возникающее в сечениях ремня при огибании шкивов (см. рис. 6.13) и изменяющееся по пульсирующему циклу. В плос­ком ремне нейтральный слой проходит посередине толщины ремня. На­ружные слои ремня при огибании шкива растягиваются, а внутренние — сжимаются. Приближенно примем, что закон Гука справедлив и для мате­риалов ремней, тогда для растянутой стороны ремня а_и = гЕ, где s = у_тт/р — относительное удлинение волокон.

С учетом того, что у_тax = 0,5δ, а р = 0,5(D₁ + 8) (см. рис. 6.12, б), пренеб­регая величиной 8 по сравнению с /),, получим:

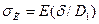(6.32)

где Е — модуль продольной упругости материала ремня; 8 — толщина рем­ня; D_x — диаметр огибаемого шкива.

В расчетах для плоскоременных передач а_и ограничивается минималь­но допустимым значением δ/D, (см. табл. 6.1).

На тяговую способность передачи напряжение изгиба не влияет, но яв­ляется основной причиной усталостного разрушения ремня.

4. Напряжение от центробежных сил. Это напряжение зависит от силы F;.

σ_v= F_v /A. (6.33)

На рис. 6.13 показано, что по всей длине ремня напряжение а₀ распре­деляется равномерно.

5. Наибольшее суммарное напряжение а_тах определяется как сумма по­лезного напряжения, напряжения изгиба в ведущей ветви (а, и а_и1) и на­пряжения от центробежных сил (σ_v):

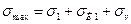(6.34)

(о_тах возникает в ремне, в месте его набегания на малый шкив (см. рис. 6.13)).

Рассмотренные напряжения в ветвях ремня используются в дальней­шем при расчете ременных передач на тяговую способность, для определе­ния максимального напряжения в ремне и т. п.

Следует отметить, что прочность ремня не является достаточным усло­вием, определяющим работоспособность ременной передачи. Желательно, чтобы передача обеспечивала как можно большее значение силы F,, при неизменном для данного ремня значении начальной силы натяжения 2F₀.

Ha каком участке ремня возникают минимальные изгибающие напря­жения?

6.28. Скольжение ремня. Как показали экспериментальные исследова­ния, упругое скольжение ремня по шкиву возникает в нормально работаю­щей передаче.

Причиной упругого скольжения является неодинаковость натяжения веду­щей и ведомой ветвей.

При обегании ремнем ведущего шкива его натяжение падает, от F_x до F₂ (причем всегда F_x > F₂) (см. шаг 6.24); ремень, проходя шкив, укорачива­ется, вследствие чего возникает упругое скольжение. На ведомом шкиве происходит аналогичное явление, но здесь ремень удлиняется, так как на­тяжение от F₂ возрастает до F_x.

Упругое скольжение происходит не по всей длине дуги обхвата ремнем шкива. Установлено, что угол дуги обхвата а разделяется на две части — дугу упругого скольжения (а_с) и дугу покоя (а_п), на которой упругое сколь­жение отсутствует (см. рис. 6.13). При перегрузке передачи скольжение происходит по дуге а = а_с + а_п, т. е. ремень скользит по всей поверхности касания со шкивом. Такой вид скольжения называют буксованием.

При упругом скольжении скорости по длине ремня неодинаковы. Скорость ремня и окружная скорость шкива совпадают лишь на дуге по­коя со стороны набегающей ветви. Это позволяет оценить упругое про­скальзывание.

Коэффициент упругого скольжения:

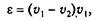(6.35)

где v₁ и v₂- окружные скорости ведущего и ведомого шкивов.

При нормальном режиме работы ременной передачи значение е = 0,01 ÷ 0,02.

На рис. 6.13 покажите дугу упругого скольжения на ведущем и ведомом шкивах. На какой ветви (набегающей или сбегающей) находятся дуги сколь­жения и покоя?

6.29.Коэффициент тяги и кривые скольжения. В результате исследова­ния кривых скольжения (рис. 6.14), построенных по опытным данным, ус­тановлена связь между полезной нагрузкой (окружной силой F) и предва­рительным натяжением ремня F_o в зависимости от коэффициента скольже­ния е.

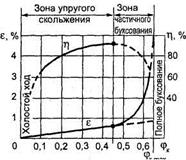Рис. 6.14.Кривые скольжения и КПД ременной передачи

Отношение передаваемой ремнем ок­ружной силы к сумме натяжений его ветвей называют коэффициентом тяги:

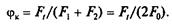(6.36)

Коэффициент тяги характеризует нагру­зочную способность передачи. На этом гра­фике (см. рис. 6.14) по оси абсцисс отложе­ны значения коэффициента тяги ф_к, а по оси ординат — коэффициент скольжения е и КПД передачи .

На начальном участке кривой скольже­ния (от 0 до ср_к) наблюдается только упру­гое скольжение. Линия этого участка приближается к прямой. Здесь зна­чения КПД и £ падают с уменьшением нагрузки. Дальнейшее увеличение нагрузки (т. е. увеличение ср_к) приводит к буксованию. В зоне частичного буксования (от ф_к0 до (р_кп1ах) наблюдаются как упругое скольжение, так и буксование.

При ф_к < ф_к0 рабочую нагрузку следует принимать в пределах, которые соответствуют наибольшему значению КПД. Работа в зоне частичного бук­сования допускается только в момент пуска передачи (т. е. для кратковре­менных перегрузок).

Для ремней:	Не более
плоских, кожаных и шерстяных прорезиненных хлопчатобумажных клиновых	1,35-1,5 1,15-1,3 1,25-1,4 1,5-1,6

Кратко охарактеризуйте работу ременной передачи в зоне частичного буксования (см. рис. 6.14).

6.30. Допускаемые напряжения в ремне.

1. Допускаемое приведенное полезное напряжение К_о. Из графика на рис. 6.14 видно, что оптимальное значение коэффици­ента тяги ф_к0 определяет максимальную полезную окружную силу F_lmm.

При этом условии ременная передача с начальным натяжением F_o может работать без пробуксовки. Из выражения (6.36)

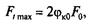(6.37)

где ф_к0 — оптимальный коэффициент тяги. Если обе части равенства (6.37) разделить на площадь поперечного сечения ремня А, то получим

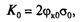(6.38)

здесь 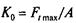— допускаемое приведенное полезное напряжение в рем­не, соответствующее коэффициенту тяги ф_к0. Значение К_ос учетом табл. 6.1 можно определить для плоскоременной передачи по формуле

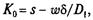
где s и да — постоянные коэффициенты, зависящие от материала ремня и о₀.

Для клиноременной передачи К_о определяется по табл. 6.6.

Таблица 6.6. Значения Kg для клиновых ремней

Диаметр малого шкива £>|, мм	Тип ремня	Ко
при сто= 1.18, МПа	при сго= 1.47, МПа
Не менее 90	Z(O)	1,42 1,54 1,62	1,59 1,71 1,82
Не менее 125	А	1,48 1,58 1,67	1,64 1,76 1,87
Не менее 180	B(Б)	1,48 1,64 1,71	1,64 1,84 2,01
Не менее 280	С(В)	1,48 1,66 1,80 1,87	1,64 1,85 2,03 2,20
Не менее 450	D(Г)	1,48 1,69 1,87 1,88	1,64 1,89 2,12 2,20

2. Допускаемое полезное напряжение в ремне К_П.

Практически значение напряжения К_о не постоянно, оно зависит от типа и толщины ремня 5, диаметра малого шкива D,, скорости ремня и, предварительного напряжения с₀ и режима работы передачи.

При проектировании ременных передач используют параметр [К]_п (до­пускаемое полезное напряжение), а не К_о. Экспериментальным путем уста­новлено, что

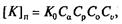(3.39)

где С_а, С_р, С_о, С„ — поправочные коэффициенты, значения которых приве­дены в табл. 6.7; эти коэффициенты учитывают: С_а — влияние угла обхвата малого шкива; С_р — режим работы передачи; С_о — вид передачи и располо­жение ее элементов; C_v — ослабление сцепления ремня со шкивом под действием центробежной силы (скоростной коэффициент).

Чем отличается параметр Kq от [К]_п?

Таблица 6.7. Коэффициенты	Са, Ср, Со, Cv расчета допускаемого полезного напряжения
Коэффициент	Условия работы	Значения
Са — угла обхвата	При угле обхвата для плоских (клиновых) ремней
	180°	1,00, (1,00)
	170°	0,96; (0,98)
	160°	0,94; (0,95)
	150°	0,91; (0,92)
	140°	-(0,89)
	130°	-(0,86)
	120°	-(0,83)
	110°	-(0,78)
	100°	-(0,74)
	80°	-(0,62)
Ср _ режима работы	При нагрузке:
	спокойной	1,0
	с умеренными колебаниями	0,9
	со значительными колебаниями	0,8
	ударной и резко неравномерной	0,7
Со __ учитывающий рас-	При угле наклона линии центров передачи
положение осей валов,	к горизонту
(перекрестной), полупе-	0-60°	1,0; (0,9);
рекрестной передачи	60-80°	0,8; 0,9;
	80-90°	(0,8); 0,7;
		0,8; (0,7);
		0,6
Су — скоростной для	При скорости ремня, (м/с):
плоских (клиновых) рем-		1,04; (1,05)
ней		1,03; (1,04)
		1,0; (1,0)
		0,95; (0,94)
		0,88; (0,85)
		0,79; (0,74)
		0,68; (0,60)

6.31.Ответить на вопросы контрольной карточки 6.3.