Определение кинематических параметров принципиальной схемы
К основным параметрам кинематической схемы относятся: мощность, частота вращения электродвигателя и фактические значения передаточных отношений всех передач. Характеристики электродвигателя определены в предыдущем пункте 3.2, а передаточное отношение определите по графику частот вращения шпинделя используя рекомендации Приложения 1.8.1.
Из рассмотрения графиков частот вращения следует, что величина передаточного отношения передач в группах зависит от их количества р, характеристики х и знаменателя ряда  . С целью ограничения радиальных размеров для зубчатых передач главного движения установлены пределы: для прямозубых
. С целью ограничения радиальных размеров для зубчатых передач главного движения установлены пределы: для прямозубых  ; для косозубых
; для косозубых 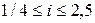 ; для механизмов подачи
; для механизмов подачи 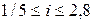 .
.
Число зубьев колес группы передач обусловлено межосевым расстоянием А, которое должно быть одинаковым для всех передач одной группы, и передаточным отношением, выраженным в форме:
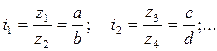 , (3.3)
, (3.3)
где 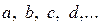 — целые числа (см. Приложение 1.8.1)
— целые числа (см. Приложение 1.8.1)
Модули зацепления прямозубых передач, нормальные модули и углы наклона зубьев косозубых колес в пределах одной группы чаще всего одинаковы, следовательно, сумма зубьев
 . (3.4)
. (3.4)
Исходя из условий компактности передач, величину 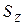 ограничивают до значения
ограничивают до значения  , а наименьшее число зубьев
, а наименьшее число зубьев 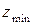 в приводах главного движения принимают более
в приводах главного движения принимают более  . Если число зубьев мало
. Если число зубьев мало  , то зубчатое колесо выполняют вместе с валом (вал-шестерня). Величину
, то зубчатое колесо выполняют вместе с валом (вал-шестерня). Величину 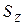 обычно принимают наименьшей допустимой с учетом числа зубьев наименьшего зубчатого колеса группы
обычно принимают наименьшей допустимой с учетом числа зубьев наименьшего зубчатого колеса группы 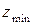 . Для сменных колёс привода установлено три значения
. Для сменных колёс привода установлено три значения 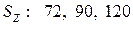
Решая уравнения относительно чисел зубьев, получим для прямозубых колёс:
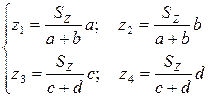 , (3.5)
, (3.5)
где 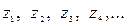 — целые числа зубьев колёс
— целые числа зубьев колёс
Это условие выполнимо, если 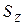 – наименьшее кратное сумм
– наименьшее кратное сумм 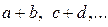 . Отсюда вытекает правило для определения чисел зубьев. Находят суммы
. Отсюда вытекает правило для определения чисел зубьев. Находят суммы
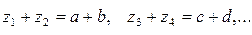 . (3.6)
. (3.6)
Затем, определяют наименьшее кратное и подставляют его вместо 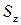 в равенство (3.5). Может оказаться, что числа зубьев получатся недопустимо малыми или большими. В первом случае их можно увеличить в целое число раз, во втором - уменьшить. При уменьшении могут появиться дробные числа зубьев. Округляя их до целого значения, отбросив дроби, изменяют
в равенство (3.5). Может оказаться, что числа зубьев получатся недопустимо малыми или большими. В первом случае их можно увеличить в целое число раз, во втором - уменьшить. При уменьшении могут появиться дробные числа зубьев. Округляя их до целого значения, отбросив дроби, изменяют  . Поэтому такие передачи подвергают коррекции.
. Поэтому такие передачи подвергают коррекции.
Если группа передач состоит из колес с разным модулем, в равенствах (3.5) величину 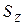 , заменяют величиной
, заменяют величиной 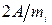 . При наличии косозубых передач с одинаковым нормальным модулем в зависимости от задания используют известную зависимость:
. При наличии косозубых передач с одинаковым нормальным модулем в зависимости от задания используют известную зависимость:
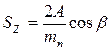 (3.7)
(3.7)
где: 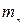 – нормальный модуль;
– нормальный модуль; 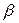 – угол наклона зуба;
– угол наклона зуба; 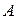 – межосевое расстояние.
– межосевое расстояние.
Подставляя значения 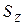 в уравнение (3.5), подучим искомые числа зубьев. Примеры расчёта чисел зубьев колес приведены в Приложении 1.9.
в уравнение (3.5), подучим искомые числа зубьев. Примеры расчёта чисел зубьев колес приведены в Приложении 1.9.
