Плоский поперечный изгиб прямого бруса
2.11.1. Общие понятия о деформации изгиба
Рассмотрим прямолинейный брус с продольной осью симметрии, нагруженный уравновешенной системой сил, линии действия которых лежат в плоскости симметрии и перпендикулярны оси бруса (рис. 2.44).
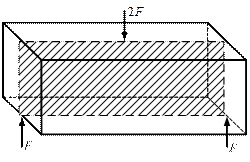
Рис. 2.44
Брус под действием этих сил изогнётся, а его продольная ось искривится. Такой вид деформации называется изгибом, а брусья, работающие на изгиб, – балками.
Деформация изгиба бруса произойдёт в плоскости действия сил (силовой плоскости), вследствие чего такой изгиб называется плоским.
При изгибе в поперечных сечениях бруса возникают внутренние моменты сил упругости, плоскость действия которых перпендикулярна плоскости поперечного сечения бруса. Эти внутренние моменты называются изгибающими моментами в сечении или просто изгибающими моментами. Если изгибающий момент является единственным внутренним усилием в сечении, то такой изгиб называют чистым. Чистый изгиб возникает под действием двух равных и противоположно направленных моментов.
В случае, когда в сечениях бруса наряду с изгибающим моментом возникает также и поперечная сила, изгиб носит название поперечного.
При плоском поперечном изгибе ось балки после деформации остаётся в плоскости действия внешних сил.
2.11.2. Опоры и опорные реакции балок
Балки служат для передачи действующих на них внешних сил (нагрузок) на опоры, на которых они установлены. В опорах возникают реакции, т.е. силы действия опор на рассматриваемую балку. Под действием внешних нагрузок и реакций опор балка находится в равновесии. Решение всех задач, связанных с деформацией изгиба, следует начинать с определения опорных реакций. В зависимости от числа и устройства опор балки число реакций, подлежащих определению, будет различно.
Опоры балок по их устройству подразделяются на три основных типа.
· Шарнирно-неподвижная опора(рис. 2.45, а).
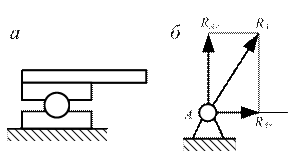
Рис. 2.45
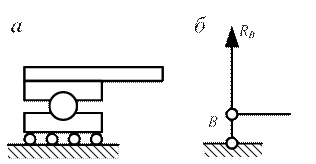
Конец балки опирается на шарнир, который расположен на неподвижной подушке. Такая опора допускает поворот конца балки, но не даёт ему возможности перемещаться в каком – либо направлении. Реакция лежит в плоскости, перпендикулярной оси шарнира, и проходит через его центр. Обычно эту реакцию раскладывают на две составляющие – вертикальную 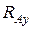 и горизонтальную
и горизонтальную 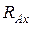 (рис. 2.45, б).
(рис. 2.45, б).
| Рис. 2.46 |
· Шарнирно-подвижная опора(рис. 2.46, а). Эта опора отличается от предыдущей тем, что у неё опорная подушка поставлена на катки, которые дают ей возможность передвигаться вместе с концом балки по направляющей. Таким образом, шарнирно-подвижная опора даёт возможность концу балки поворачиваться вокруг оси шарнира и перемещаться вдоль плоскости качения и накладывает на конец балки одну связь – не даёт возможности перемещаться в направлении, перпендикулярном направляющей (плоскости качения). Следовательно, такая опора даёт лишь одну составляющую реакции, неизвестную по величине и известную по направлению. Реакция проходит через центр шарнира и направлена перпендикулярно направляющей. В дальнейшем шарнирно – подвижную опору будем изображать, как показано на рис. 2.46, б.
· Жёсткая заделка, или защемление(рис. 2.47). Такое устройство опоры не допускает ни угловых, ни линейных перемещений защемлённого конца балки. В жёсткой заделке возникают реакция, неизвестная по величине и направлению, и реактивный момент, препятствующий повороту конца балки.
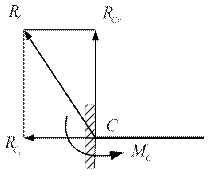 Рис. 2.47 Рис. 2.47 |
Обычно реакцию Rc заменяют двумя составляющими – вертикальной 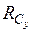 и горизонтальной
и горизонтальной 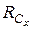 . Таким образом, можно отметить, что жёсткая заделка даёт три неизвестные реакции: вертикальную и горизонтальную составляющие и реактивный момент.
. Таким образом, можно отметить, что жёсткая заделка даёт три неизвестные реакции: вертикальную и горизонтальную составляющие и реактивный момент.
В технике балку с одним защемлённым концом называют консольной балкой, или консолью.
В случае, когда все внешние силы, действующие на балку, направлены перпендикулярно её оси, число неизвестных реакций уменьшается, так как в шарнирно-неподвижной опоре и в жёсткой заделке составляющая реакции, направленная вдоль оси балки, будет равна нулю.
2.11.3. Определение опорных реакций
В случае действия на балку плоской системы сил можно записать три уравнения равновесия:
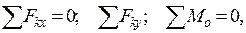
откуда следует: для равновесия балки необходимо, чтобы суммы проекций всех сил, приложенных к балке, включая реакции опор на оси x и y, и сумма моментов всех сил относительно любого полюса в плоскости действия сил были равны нулю.
 Рис. 2.48 Рис. 2.48 |
Если опорные реакции балок могут быть найдены из уравнений статики, то балки называют статистически определимыми. Они могут быть только двух видов:
· балка с одним жестко защемлённым и одним свободным концом (консоль) (рис. 2.48, а);
· балка с одной шарнирно-неподвижной и другой шарнирно-подвижной опорой (рис. 2.48, б, в). Балка, изображённая на рис. 2.48, б называется простой, а балка на рис. 2.48, в – консольной, так как имеет свешивающиеся с опор концы, которые называются консолями.
Пример 1
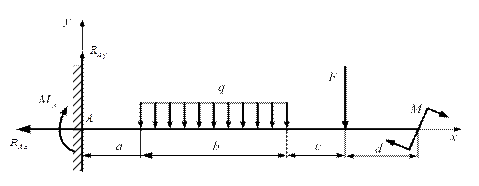 Рис. 2.49 Рис. 2.49 |
Определить опорные реакции консольной балки (рис. 2.49).
Решение. Реакцию заделки представляем в виде двух составляющих – вертикальной 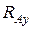 и горизонтальной
и горизонтальной 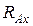 и реактивного момент а MA; при этом направления сил вдоль осей и направление момента принимаем произвольно. Условимся здесь и в дальнейшем ось x направлять вправо, а ось у – вверх.
и реактивного момент а MA; при этом направления сил вдоль осей и направление момента принимаем произвольно. Условимся здесь и в дальнейшем ось x направлять вправо, а ось у – вверх.
Составляем уравнение равновесия:
· Сумма проекций всех сил на горизонтальную ось x равна нулю: 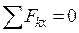 . Из этого уравнения получаем, что
. Из этого уравнения получаем, что 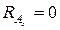 , т. е. при отсутствии горизонтальной нагрузки горизонтальная составляющая реакции равна нулю;
, т. е. при отсутствии горизонтальной нагрузки горизонтальная составляющая реакции равна нулю;
· Сумма проекций всех сил на вертикальную ось у равна нулю: 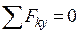 . Равномерно распределённую нагрузку интенсивностью q заменяем её равнодействующей q·b, приложенной в середине участка b:
. Равномерно распределённую нагрузку интенсивностью q заменяем её равнодействующей q·b, приложенной в середине участка b:
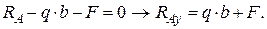
· Сумма моментов всех сил относительного любого центра равна нулю. За центр примем точку 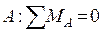 .
.
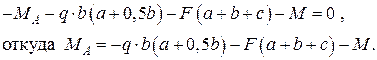
Реактивный момент получился со знаком минус, следовательно, его направление необходимо заменить на противоположное (против направления вращения часовой стрелки).
Пример 2
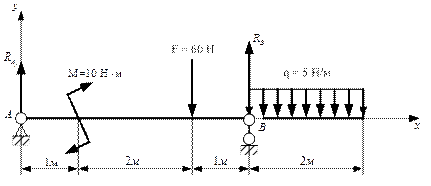 |
Определить опорные реакции двухопорной одноконсольной балки (рис. 2.50).
Рис. 2.50
Решение. Поскольку горизонтальная нагрузка отсутствует, то
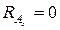 .
.
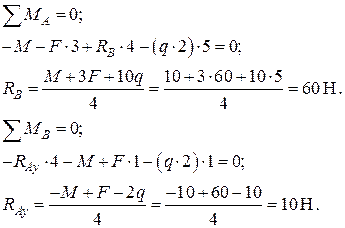
В качестве проверочного воспользуемся уравнением проекций всех сил на вертикальную ось 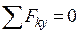 :
:
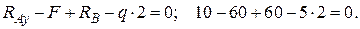
2.11.4. Поперечная сила и изгибающий момент в сечении
При плоском поперечном изгибе в любых поперечных сечениях балки возникают два внутренних силовых фактора – поперечная сила Q и изгибающий момент MИ. Для их определения, как и при других видах деформаций, применим универсальный метод, который называется методом сечений.
Мысленно рассечём балку по сечению n-n, находящемуся на расстоянии x от левой опоры A (рис. 2.51, а). Правую часть балки отбросим и рассмотрим равновесие оставшейся левой части (рис. 2.51, б). Для того чтобы она находилась в равновесии, в сечении должны действовать поперечная сила и изгибающий момент, представляющие собой действие отброшенной части на оставшуюся. Для определения Q и MИзапишем два уравнения равновесия:
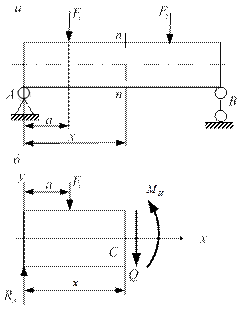 |
Рис. 2.51
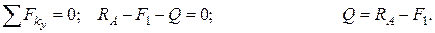
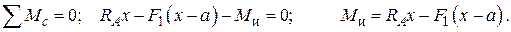
Из полученных выражений сформулируем правила определения Q и Mи.
. Результирующая внутренних сил, приложенная в сечении оставшейся части балки, численно равна алгебраической сумме внешних сил, действующих по одну сторону от сечения, называется поперечной силой и обозначается Q.
Момент пары внутренних сил, приложенный к оставшейся части балки, численно равный алгебраической сумме моментов внешних сил, действующих по одну сторону от сечения, называется изгибающим моментом и обозначается MИ.
Если вместо левой части балки рассмотреть правую, то изгибающий момент и поперечная сила в сечении будут иметь те же значения, но иметь противоположные знаки.
Для того чтобы изгибающий момент и поперечная сила в одном и том же сечении имели один знак независимо от того, к какой части они приложены, введём следующие правила знаков.
Поперечная сила в сечении балки n-n (рис. 2.52, а) считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа от сечения – сверху вниз.
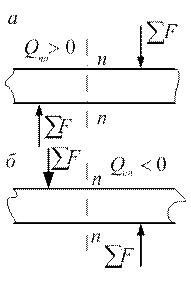 Рис. 2.52 Рис. 2.52 |
В противоположном случае поперечная сила Q в сечении n-n будет считаться отрицательной (рис. 2.52, б).
Изгибающий момент в сечении m-m (рис. 2.53, а) считается положительным, если равнодействующий момент внешних сил слева от сечения направлен по часовой стрелке, а справа от сечения – против. При направлении равнодействующих внешних моментов справа и слева от рассматриваемого сечения в другом направлении момент в сечении считается отрицательным (рис. 2.53, б).
Из рис. 2.53 следует, что изгибающий момент считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз, отрицательным – если выпуклостью вверх. Волокна балок, расположенные в вогнутой части, испытывают сжатие, а в выпуклой – растяжение. При построении эпюр изгибающих моментов положительные ординаты откладывают вверх от базовой оси, таким образом, эпюра будет построена со стороны сжатых волокон балки.
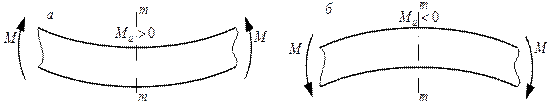
Рис. 2.53
2.11.5. Зависимость между изгибающим моментом, поперечной силой и интенсивностью распределённой нагрузки
Рассмотрим балку, нагруженную силами F1, F2, F3. Опорные реакции – RA и RB (рис. 2.54). Запишем момент в сечении n-n от сил, лежащих левее сечения:
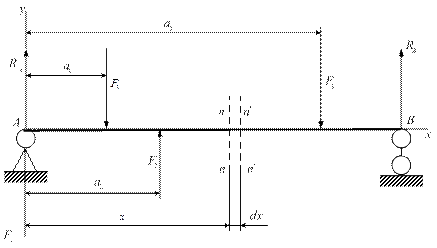
Рис. 2.54
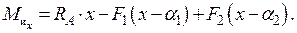
Поперечная сила в этом сечении равна алгебраической сумме внешних сил, приложенных слева от сечения:
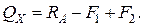
Индекс «х» у изгибающего момента и поперечной силы означает, что они являются функциями абсциссы x.
Определим значение момента в сечении n`-n`, расположенного на расстоянии dx от первого сечения:
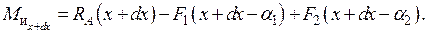
Приращение момента:
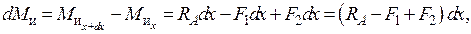
т. е. dMи=Qxdx, откуда:
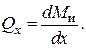 (2.80)
(2.80)
Поперечная сила в сечении равна первой производной от изгибающего момента по абсциссе сечения.
Этот вывод справедлив и при наличии равномерно распределённой нагрузки q.
Рассмотрим балку, нагруженную равномерно распределённой нагрузкой q и силами F1 и F2(рис. 2.55). Если в сечении n-n поперечная сила равна Qx, то в сечении, расположенном на расстоянии dx от рассматриваемого, поперечная сила будет равна Qx+dQx, где dQx = q·dx. Следовательно:
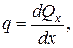 (2.81)
(2.81)
т. е. производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.
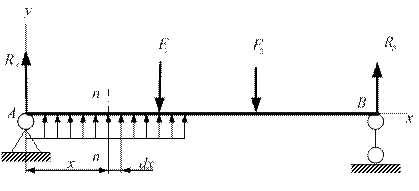 Рис. 2.55 Рис. 2.55 |
Возьмём производную от обеих частей равенства (2.81) и получим
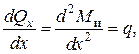 (2.82)
(2.82)
т. е. вторая производная от изгибающего момента по абсциссе сечения равна интенсивности распределённой нагрузки.
Зависимости (2.81) и (2.82) выведены русским учёным Д.И. Журавским и используются при построении эпюр поперечных сил и изгибающих моментов.
2.11.6. Построение эпюр поперечных сил и изгибающих моментов
Нормальные и касательные напряжения, возникающие в поперечных сечениях балки, зависят от изгибающих моментов Ми и поперечных сил Q. Для определения опасных сечений и наглядного представления о характере изменения Мии Q по длине балки строят графики, которые называются эпюрами изгибающих моментов и поперечных сил. Чтобы усвоить технику их построения, рассмотрим пример.
Построить эпюры Q и Ми для балки, представленной на рис. 2.56, а.
Решение
1. Определение опорных реакций:
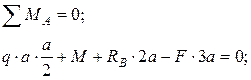
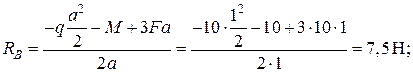
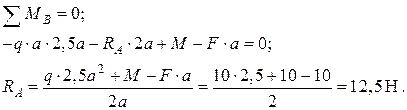
Проверка: 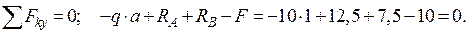
2. Построение эпюры поперечных сил «Q» (рис. 2.56, б). Характерными сечениями разбиваем балку на четыре участка. Сечения проводим по краям балки, а также через точки приложения сосредоточенных сил и моментов, а также в начале и конце участков с распределённой нагрузкой. Поперечную силу в пределах каждого участка будем записывать в виде уравнения, аргументом которого является переменная координата х. Поперечную силу находим в соответствии с правилом как алгебраическую сумму внешних сил, действующих слева от рассматриваемого сечения. Индекс у поперечной силы обозначает номер участка.
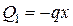 – это уравнение прямой линии, которую можно построить по двум точкам. Определяем значение Q в начале и конце участка.
– это уравнение прямой линии, которую можно построить по двум точкам. Определяем значение Q в начале и конце участка.
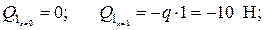
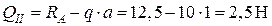 . В любом сечении участка АС поперечная сила имеет одно и то же значение, эпюра будет изображаться линией, параллельной базовой оси.
. В любом сечении участка АС поперечная сила имеет одно и то же значение, эпюра будет изображаться линией, параллельной базовой оси.
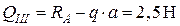 . Характер эпюры тот же, что и на участке АС.
. Характер эпюры тот же, что и на участке АС.
Для определения Q на участке BD удобнее отбросить левую часть и рассмотреть оставшуюся правую. 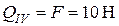 .
.
Проводим базовую ось параллельно оси балки и в масштабе строим эпюру поперечных сил на каждом участке в соответствии с уравнениями (рис. 2.56. б).
3. Построение эпюры изгибающих моментов МИ (рис. 2.56, в). Изгибающие моменты также определяются по участкам и записываются в виде уравнений, в которых независимой переменной является координата х:
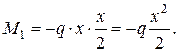
Уравнение изгибающих моментов на участке ОА является уравнением второго порядка. Для построения эпюры необходимо определить моменты трёх или более точек. Определим МИ в начале, конце и в середине первого участка:
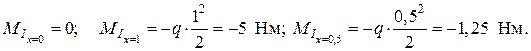
Изгибающий момент на втором участке АС определим как алгебраическую сумму моментов внешних сил слева от сечения с координатой xII:
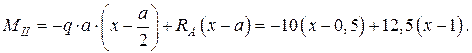
Получили уравнение прямой линии, которую можно построить по двум точкам, соответствующим двум значениям изгибающего момента. Находим эти значения в начале и конце участка АС:
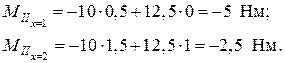
Уравнение моментов для участка CD также запишем, суммируя моменты внешних сил, расположенных слева от сечения xIII:

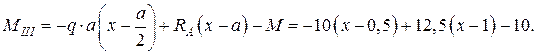
Определим значения изгибающих моментов на границах участка CB:
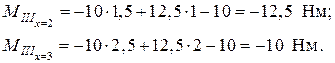
Для определения изгибающих моментов на четвёртом участке удобнее отбросить левую часть балки, так как к ней приложено большее число внешних сил:
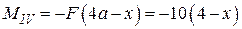 .
.
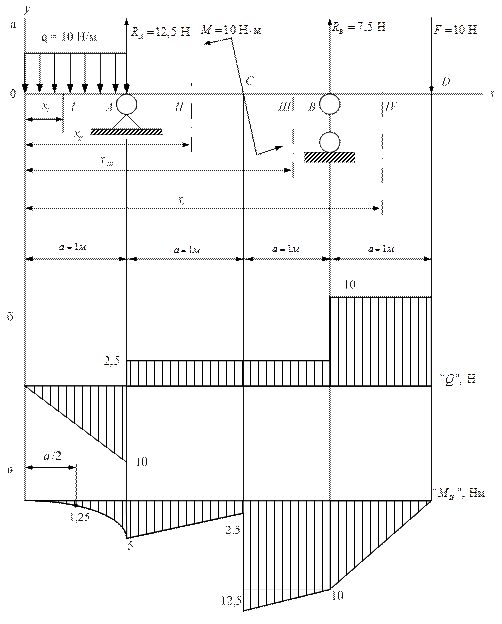
Рис. 2.56
Значения моментов на границах участка:
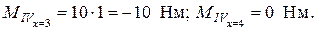
Строим в масштабе эпюру «Ми» на каждом участке в соответствии с полученными уравнениями (см. рис. 2.56).
Анализируя эпюры «Q» и «Ми», можно отметить следующие зависимости между характером эпюр и нагрузок:
· на участке с равномерно распределённой нагрузкой эпюра поперечных сил очерчивается наклонной прямой линией, а эпюра изгибающих моментов имеет криволинейное очертание – квадратичную параболу;
· между точками приложения сосредоточенных сил поперечная сила постоянна, а эпюра моментов очерчивается наклонной прямой линией;
· эпюра поперечных сил скачкообразно изменяется в местах приложения внешних сил, при этом величина скачка равна приложенной сосредоточенной силе;
· сосредоточенный момент не влияет на характер эпюры поперечных сил, а на эпюре изгибающих моментов в этом сечении имеется скачок, величина которого равна приложенному внешнему моменту;
· поперечная сила Q положительна на участках балки, где эпюра Ми восходящая, если смотреть слева направо, и отрицательна на тех участках, где эпюра Ми нисходящая;
· поскольку Q = dM/dx то изгибающий момент достигает экстремума (максимума или минимума) в тех сечениях, где поперечная сила равна нулю, т.е. эпюра Q пересекает базовую ось.
Перечисленные зависимости используются для контроля правильности построения эпюр внутренних силовых факторов при деформации изгиба.
2.11.7. Определение нормальных напряжений при изгибе
Метод сечений даёт возможность определить поперечную силу и изгибающий момент в сечении. Выяснение же закона распределения напряжений по сечению можно выполнить только на основании рассмотрения деформаций.
Если подвергнуть чистому плоскому изгибу балку с нанесённой на поверхность сеткой (рис. 2.57. а, б), то можно сделать следующие выводы:
· линии n-n и m-m на поверхности балки после деформации повернулись на угол dφ, оставаясь при этом прямыми. Прямые углы сетки не изменились. Это свидетельствует о том, что касательные напряжения в поперечных сечениях равны нулю;
· волокно ab удлинилось, волокно ef укоротилось, а cd осталось без изменения. Слой балки на уровне волокна cd называется нейтральным слоем.
Можно также заметить, что волокна балки деформируются по – разному; большие деформации у волокон, наиболее удалённых от нейтрального слоя.
Определим закон изменения деформации по высоте сечения балки.
Отрезок b'b" является полным удлинением волокна ab, длина которого до деформации была равна длине волокна cd, принадлежащего нейтральному слою.
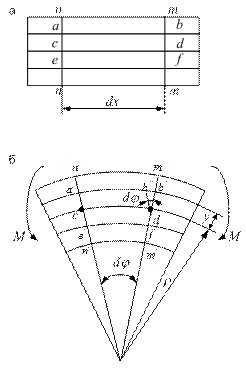
Рис. 2.57
Относительная деформация:
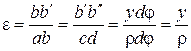 , где ρ – радиус кривизны нейтрального слоя; y – расстояние от нейтрального слоя до рассматриваемого волокна.
, где ρ – радиус кривизны нейтрального слоя; y – расстояние от нейтрального слоя до рассматриваемого волокна.
Поскольку волокно бруса при изгибе растягивается или сжимается, применим закон Гука:
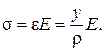 (2.83)
(2.83)
В соответствии с формулой (2.83) нормальные напряжения при изгибе изменяются по высоте поперечного сечения балки пропорционально расстоянию от нейтральной оси. Наибольшие напряжения будут у верхнего и нижнего краёв сечения, как это показано на эпюре (рис. 2.58).
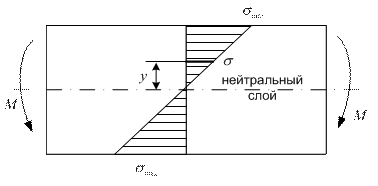
Рис. 2.58
Установив закон распределения напряжений, можно их определить, исходя из условия равновесия.
Выделим в площади поперечного сечения элементарную площадку dA, отстоящую на расстоянии у от нейтральной оси, проходящей через нейтральный слой (рис. 2.59). Нормальная элементарная сила, действующая на этой площадке с учётом выражения (2.83):

Рис. 2.59
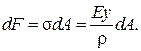 (2.84)
(2.84)
Для равновесия рассматриваемой части балки (см. рис. 2.59) необходимо, чтобы суммы проекций всех сил на координатные оси x, y и z и суммы моментов относительно этих осей были равны нулю ( 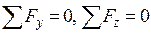 ), так как внутренние силы σdA перпендикулярны этим осям;
), так как внутренние силы σdA перпендикулярны этим осям; 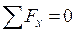 или, с учётом уравнения (2.84),
или, с учётом уравнения (2.84), 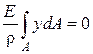 . Отношение E/ρ не может быть равно нулю, так как отличны от нуля и модуль упругости Е, и кривизна нейтрального слоя.
. Отношение E/ρ не может быть равно нулю, так как отличны от нуля и модуль упругости Е, и кривизна нейтрального слоя.
Следовательно, интеграл:
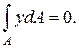
Он представляет собой статический момент площади поперечного сечения относительно нейтральной оси. Статический момент равен нулю в том случае, если он взят относительно центральной оси, проходящей через центр тяжести сечения. Отсюда следует важный вывод о том, что нейтральная ось всегда проходит через центр тяжести поперечного сечения балки.
Элементарный момент внутренний силы, действующей на площадке dA относительно нейтральной оси z:
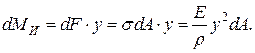
Сумма всех элементарных моментов внутренних сил упругости по условию равновесия равна внешнему моменту, т.е.:
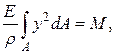
где 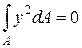 – момент инерции поперечного сечения балки относительно нейтральной оси z.
– момент инерции поперечного сечения балки относительно нейтральной оси z.
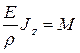 , откуда:
, откуда:
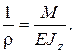 (2.85)
(2.85)
Формула (2.85) является основной формулой теории изгиба. Величина 1/ρ представляет собой кривизну изогнутой оси балки и характеризует величину деформации при изгибе.
Из полученной формулы следует, что деформация при изгибе прямо пропорциональна изгибающему моменту и обратно пропорциональна произведению EJz, которое называется жёсткостью балки при изгибе.
Подставим значения 1/ρ в формулу (2.84):
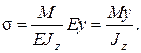 (2.86)
(2.86)
Формула (2.86) позволяет определить нормальное напряжение в любой точке поперечного сечения балки, если известны изгибающий момент и момент инерции сечения.
На отсечённую часть балки может действовать не один внешний момент, как на рис. 2.59, а несколько, а также любая другая нагрузка в виде сосредоточенных сил и распределённых нагрузок. В этом случае уравнение равновесия 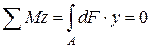 содержит алгебраическую сумму моментов от всех внешних нагрузок, равную изгибающему моменту в сечении Ми. Поэтому в дальнейшем вместо суммы внешних моментов в формулы следует подставлять изгибающий момент в сечении.
содержит алгебраическую сумму моментов от всех внешних нагрузок, равную изгибающему моменту в сечении Ми. Поэтому в дальнейшем вместо суммы внешних моментов в формулы следует подставлять изгибающий момент в сечении.
Формула (2.86) соответствует чистому изгибу. При поперечном изгибе в поперечных сечениях кроме нормальных действуют и касательные напряжения, вызывающие деформацию сдвига. Вследствие этого гипотеза плоских сечений теряет свою силу. Однако опыт показывает, что, несмотря на это, формула (2.86) даёт достаточно точные результаты и при поперечном изгибе, поэтому в дальнейшем при определении нормальных напряжений не следует делать различия между чистым и поперечным изгибом.
2.11.8. Условие прочности по нормальным напряжениям
Согласно уравнению (2.86) наибольшие нормальные напряжения, могущие привести к разрушению, возникают в волокнах, наиболее удалённых от нейтральной оси. Так как при прочностных расчётах определяются максимальные напряжения, то в формуле (2.86) вместо текущего значения у подставляют расстояние от нейтральной оси до наиболее удалённых волокон.
Наибольшие напряжения растяжения: 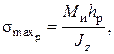
где hp – расстояние от нейтральной оси до наиболее удалённых волокон в растянутой зоне.
Наибольшие напряжения сжатия:
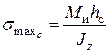 , где hc – расстояние от нейтральной оси до наиболее удалённых сжатых волокон.
, где hc – расстояние от нейтральной оси до наиболее удалённых сжатых волокон.
Таким образом, при несимметричном профиле, когда yp не равно yc и если материал балки по – разному реагирует на растяжение и сжатие, то условие прочности запишется следующим образом:
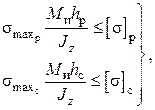 (2.87)
(2.87)
где [σ]P и [σ]C – допускаемые напряжения при растяжении и сжатии соответственно.
Если профиль балки симметричный, т. е. hc= hp, а также в случае, когда материал одинаково сопротивляется и растяжению и сжатию, то достаточно определить только максимальное напряжение для тех волокон, которые наиболее удалены от нейтральной оси:
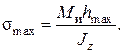
Если величина изгибающего момента по длине бруса меняется, то для определения максимальных напряжений необходимо брать то сечение, в котором действует максимальный момент. Такое сечение бруса называется опасным сечением.
Отношение момента инерции сечения относительно нейтральной оси Jz к расстоянию ymax наиболее удалённого от этой оси волокна называется моментом сопротивления сечения при изгибе и обозначается Wz или в общем виде Wи:
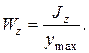 (2.88)
(2.88)
Таким образом, в случае симметричного относительно нейтральной оси сечения балки, т. е. при hp = hс = h/2 или при одинаковых допускаемых напряжениях на растяжение и сжатие [σ], вместо двух формул (2.87) получим одну, выражающую условие прочности по нормальным напряжениям при изгибе:
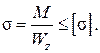 (2.89)
(2.89)
Для стандартных профилей проката, таких как швеллер, двутавр, уголок, значения осевых моментов сопротивления приведены в таблицах сортамента.
Для прямоугольного сечения:
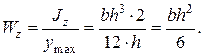 (2.90)
(2.90)
Для квадратного сечения со стороной а:
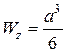 . (2.91)
. (2.91)
Для круглого сечения:
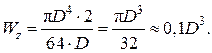 (2.92)
(2.92)
Для кольцевого сечения с наружным диаметром D и внутренним d:
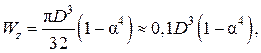 (2.93)
(2.93)
где α = d/D.
Используя уравнение (2.89), можно подобрать сечение профиля, исходя из условия прочности по нормальным напряжениям. Определим требуемый осевой момент сопротивления:
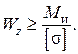 (2.94)
(2.94)
Затем по таблицам стандартных прокатных профилей или в соответствии с формулами (2.90) – (2.94) в зависимости от задания выбираем или рассчитываем сечение.
