Понятия о линии и полюсе зацепления. Профилирование зубьев

3.15. Для обеспечения нормальной работы пары зубчатых колес с по-:тоянным передаточным числом профили зубьев должны быть очерчены ~о кривым, подчиняющимся определенным законам. Эти законы вытека­ют из основной теоремы зацепления, сущность которой заключается в сле-гующем.

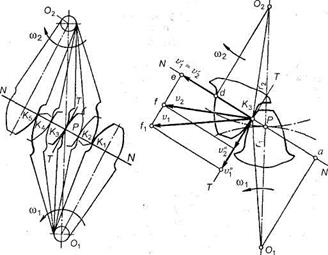
Пусть имеется пара зубчатых колес с центрами О₁ и О₂, вращающихся :эответственно с угловыми скоростями со, и со₂. На рис. 3.18, а показаны г сложения, которые последовательно занимает пара сопряженных (эволь-нгнтных) зубьев в процессе их зацепления; прямую О₁О₂ называют межосе-еой линией зубчатой передачи. Проведем в точках касания зубьев К₁, К₂,

а) б)

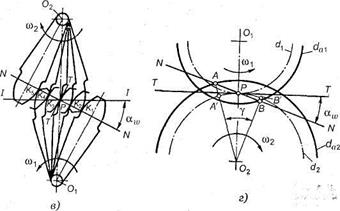
Рис. 3.18.Элементы зубчатого зацепления

К_г, ... общие нормали к профилям. Все эти нормали NN должны пересекать межосевую линию О₁ О₂ в постоянной точке Р. Эту точку называют полюсом зацепления; ее положение на межосевой линии определяется отношением уг­ловых скоростей колес, т. е. их отношением:

.

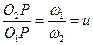Основную теорему зацепления можно сформулировать так: общая нор­маль к профилям зубьев в точке их касания пересекает межосевую линию в точке Р, называемой полюсом зацепления и делящей межосевое расстояние не отрезки, обратно пропорционально угловым скоростям.

Следствие: для обеспечения постоянного передаточного отношения по­ложение полюса Р на линии центров должно быть постоянным.

3.16. В процессе работы сопряженных (эвольвентных) профилей точка их касания все время перемещается по прямой NN. Эту прямую называют линией зацепления.

Место (точку) входа в зацепление и выхода из него сопряженных зубь­ев можно определить при следующем геометрическом построении.

Возьмем произвольное межосевое расстояние О₁ О₂ (рис. 3.18, г) и раз­делим его в произвольном отношении O₂P/O₁P = и. Радиусами О₂Р и O₁P проведем начальные окружности зубчатых колес через точку Р, касатель­ную ТТ к этим окружностям и линию NN — нормаль к боковым поверхно­стям зубьев — под углом а_ω и касательной ТТ. Угол a_ω называют углом за­цепления; в СНГ а_ω принят 20°.

Примем произвольную высоту головки зубьев и проведем радиусами. равными 1/2d_a1 и 1/2d_a2, окружности выступов зубчатых колес (высота го­ловки зуба шестерни и колеса должна быть одинаковой). При направлении вращения колес, указанном на рисунке, зубья войдут в зацепление в точке А (точке пересечения нормали с окружностью выступов колеса) и выйду: из зацепления в точке В (точке пересечения нормали с окружностью вы­ступов шестерни).

Все точки касания сопряженных зубьев будут лежать на участке АВ ли­нии зацепления. Участок АВ называется рабочим участком линии зацепле­ния.

Необходимое условие непрерывности зацепления: дуга зацепления должна быть больше шага. В противном случае при выходе из зацепления одной пары зубьев вторая пара еще не войдет.

Длина линии зацепления q_a — отрезок линии зацепления, отсекаемы;: окружностями вершин зубьев сопряженных колес. Он определяет начало у. конец зацепления пары сопряженных зубьев. Длина зацепления — актив­ная часть линии зацепления.

Коэффициент торцового перекрытия ε_a — отношение длины линии за­цепления к шагу:

.

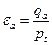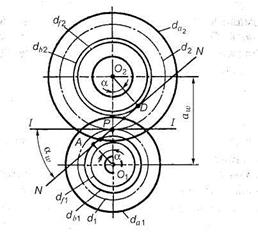
Рис. 3.19. Геометрические параметры зубчатой передачи

Можно ли увидеть на зубчатом колесе (рис. 3.19) линию зацепления NN и угол зацепления a_w или это только теоретически представляемые геометри­ческие элементы?

3.17.Полюс зацепления Р (см. рис. 3.18, б) сохраняет неизменное положе­ние на линии центров 0₁0₂. Следовательно, радиусы 0₁Р (r₁) и 0₂Р (r₂) также неизменны. Окружности радиусов r₁ и r₂ называют начальными (делитель­ными — см. шаг 3.13). При вращении зубчатых колес эти окружности пе­рекатываются одна по другой без скольжения, о чем свидетельствует ра­венство их окружных скоростей ω₁ r₁ = ω₂r₂ (см. доказательство основной теоремы зацепления). Теоретически боковые поверхности зубьев (профи­ли) могут быть очерчены любыми кривыми, удовлетворяющими основному закону зубчатого зацепления. Такие профили называют сопряженными.
В современном машиностроении для построения сопряженных профилей применяют ограниченное число кривых.