Проверка прочности валов

Прочность валов проверим по гипотезе наибольших касательных напряжений.

Быстроходный (ведущий) вал.

Так как быстроходный вал изготовляют вместе с шестерней, то его материал известен – сталь 45, для которой предел выносливости, по формуле,[3, стр.195];

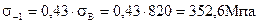(2.60)

σ_В – предел прочности, МПа. Согласно рекомендациям [3, табл. П3], предел прочности σ_В = 820 МПа.

Допускаемое напряжение изгиба при симметричном цикле напряжений, согласно рекомендациям, [3, стр. 195], определяется по формуле;

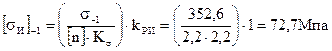(2.61)

σ_-1 – предел выносливости,

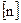– коэффициент запаса прочности ( 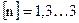),[3, стр.195];

K_σ – эффективный коэффициент концентрации напряжений (K_σ = 1,2…2,5),
по [3, стр. 195],

k_РИ – коэффициент режима нагрузки при расчете на изгиб (k_РИ = 1…1,65) по
[3, стр. 310].

Вычерчиваем схему нагружения вала и строим эпюры изгибающих и крутящих моментов (рис 2.1);

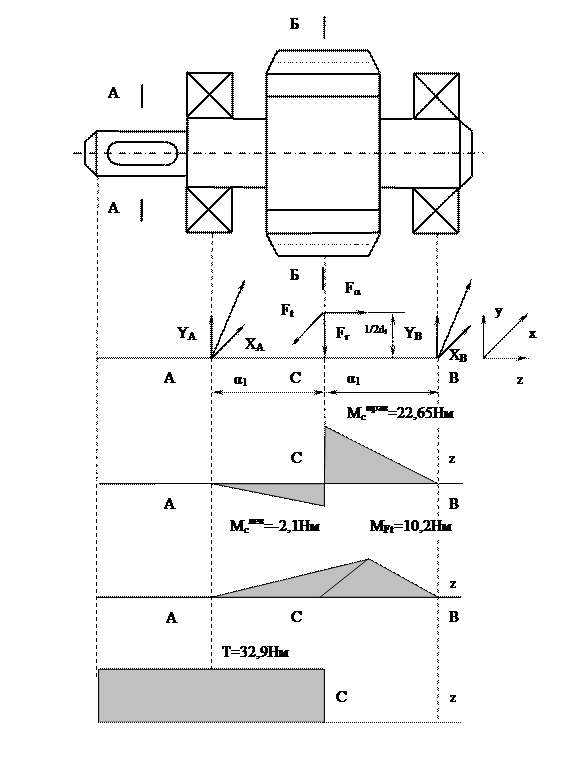Рис.П.2.1.

а) определяем реакции опор в вертикальной плоскости zOy от сил F_r и F_α;

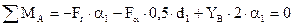(2.62)

α₁ – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала,

Fr – радиальная сила, сжимающая зуб,

Fa – осевая сила,

d₁ – делительный диаметр шестерни.

Тогда из уравнения (2.62) получаем;

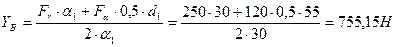	(2.63)
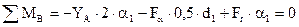	(2.64)

Тогда из уравнения (2.64) получаем;

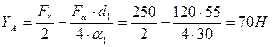(2.65)

б) определяем реакции опор в горизонтальной плоскости xOy от силы Ft;

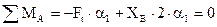(2.66)

a₁ – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала,

Ft – окружная сила, изгибающая зуб.

Тогда из уравнения (2.66) получаем;

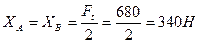(2.67)

в) для построения эпюр определяем размер изгибающих моментов в характерных точках (сечениях) А, С и В;

в плоскости yOz;

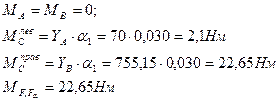(2.68)

в плоскости xOz;

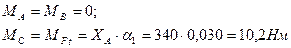(2.69)

г) крутящий момент Т = Т₁ = 168.2 Нм.

д) выбираем коэффициент масштаба и строим эпюры (рис.2.1).

Вычисляем наибольшие напряжения изгиба и кручения для опасного сечения С. Суммарный изгибающий момент по [3, стр. 311], определяется по формуле;

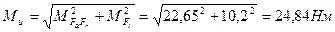(2.70)

где М_FrFa и M_Ft – изгибающие моменты.

Напряжение изгиба, по [3, стр. 311], определяется по формуле;

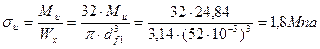(2.71)

М_И – суммарный изгибающий момент,

W_X – осевой момент сопротивления круглого сечения вала; ,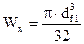

d_f1 – диаметр впадин шестерни.

Допускаемое касательное напряжение на кручение определяется, по
[3, стр. 311];

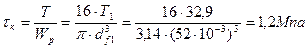(2.72)

Т – крутящий момент,

W_Р – полярный момент сопротивления круглого сечения вала; ,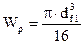

d_f1 – диаметр впадин шестерни.

Согласно рекомендациям [3, стр. 194], определяем эквивалентное напряжение по гипотезе наибольших касательных напряжений;

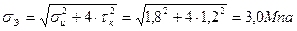(2.73)

σ_И – напряжение изгиба,

τ_К – касательное напряжение на кручение.

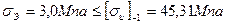(2.74)

[σ_и]_-1 – допускаемое напряжение.

Тихоходный вал (ведомый вал).

Материал для изготовления тихоходного вала – сталь 35, для которой по
[3,табл. П3] при d < 100 мм предел прочности σ_В = 510 МПа.

Предел выносливости, согласно рекомендациям [3, стр.195] определяется по формуле;

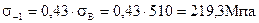(2.75)

σ_В – предел прочности.

Допускаемое напряжение изгиба при симметричном цикле напряжений, согласно рекомендациям [3, стр. 195], определяется по формуле;

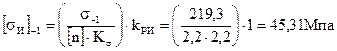(2.76)

σ_-1 – предел выносливости,

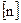– коэффициент запаса прочности ( 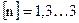),[3, стр.195];

K_σ – эффективный коэффициент концентрации напряжений (K_σ = 1,2…2,5),
по [3, стр. 195],

k_РИ – коэффициент режима нагрузки при расчете на изгиб (k_РИ = 1…1,65) по
[3, стр. 310].

Вычерчиваем схему нагружения вала и строим эпюры изгибающих и крутящих моментов (рис. 2.2);

а) определяем реакции опор в вертикальной плоскости yOz от сил F_r и F_а;

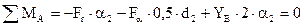(2.77)

α₂ – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала,

Fr – радиальная сила, сжимающая зуб,

Fa – осевая сила,

d₂ – делительный диаметр шестерни.

Тогда из уравнения (2.77) получаем;

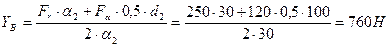	(2.78)
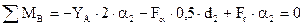	(2.79)

Тогда из уравнения (2.79) получаем;

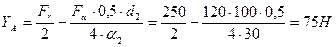(2.80)

б) определяем реакции опор в горизонтальной плоскости xOy от силы Ft;

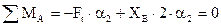(2.81)

a₂ – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, принятые на уровне внутренних торцов подшипников в точках А и В оси вала,

Ft – окружная сила, изгибающая зуб.

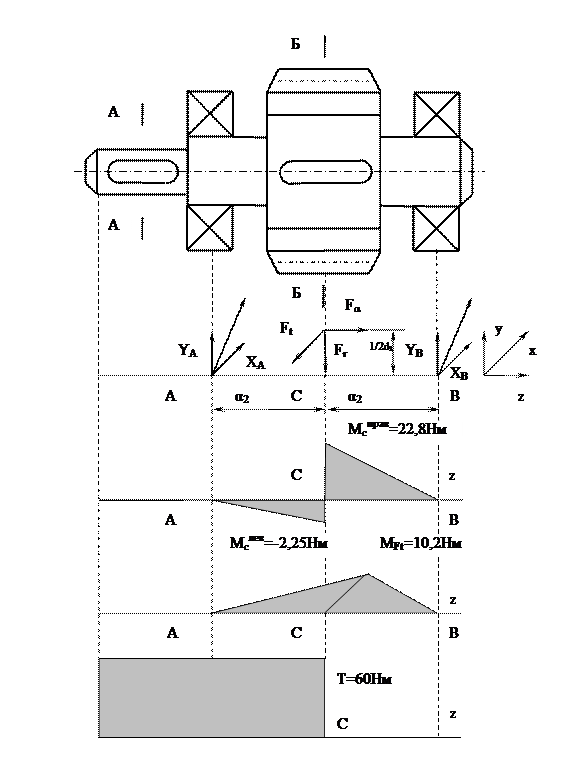Рис.П.2.2.

Тогда из уравнения (2.81) получаем;

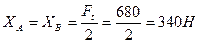(2.82)

в) для построения эпюр определяем размер изгибающих моментов в характерных точках (сечениях) А, С и В;

в плоскости yOz;

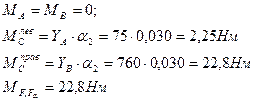(2.83)

в плоскости xOz;

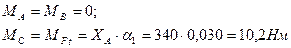(2.84)

г) крутящий момент Т = Т₂ = 168.2 Н∙м;

д) выбираем коэффициент масштаба и строим эпюры (рис.2.2.).

Вычисляем наибольшие напряжения изгиба и кручения для опасного сечения С. Суммарный изгибающий момент по [3, стр. 312], определяется по формуле;

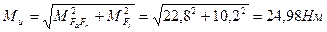(2.85)

М_FrFa и M_Ft – изгибающие моменты.

Напряжение изгиба, по [3, стр. 312], определяется по формуле;

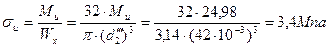(2.86)

М_И – суммарный изгибающий момент,

W_X – осевой момент сопротивления круглого сечения вала; ,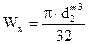

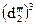– диаметр вала под посадку ступицы зубчатого колеса. Диаметр вала в опасном сечении d₂^''' = 46 мм, ослаблен шпоночной канавкой. Поэтому в расчет вводим значение d, меньшее на 8…10% d₂^'''. Принимаем расчетный диаметр вала в опасном сечении d = 42 мм.

Допускаемое касательное напряжение на кручение определяется, по
[3, стр. 312];

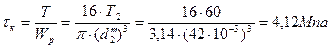(2.87)

Т – крутящий момент,

W_Р – полярный момент сопротивления круглого сечения вала; ,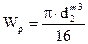

d – расчетный диаметр вала в сечении С.

Согласно рекомендациям [3, стр. 194], определяем эквивалентное напряжение по гипотезе наибольших касательных напряжений;

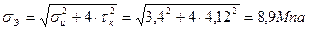(2.88)

σ_И – напряжение изгиба,

τ_К – касательное напряжение на кручение.

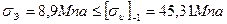(2.89)

[σ_и]_-1 – допускаемое напряжение.

При полученных невысоких значениях расчетных напряжений, валы имеют высокие значения коэффициентов запаса прочности, а поэтому проверку их жесткости можно не выполнять.