Зубчатые передачи с зацеплением Новикова. Устройство, основные геометрические соотношения

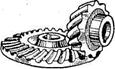
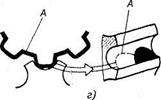
3.82. Передачи с зацеплением Новикова состоят из двух цилиндрических косозубых колес (рис. 3.57, а) или конических колес (рис. 3.57, б) с винто­выми зубьями и служат для передачи момента между валами с параллель­ными или пересекающимися осями. Особенность зацепления Новикова состоит в том, что в этом зацеплении первоначальный линейный контакт (рис. 3.57, в) заменен точечным, превращающимся под нагрузкой в контакт .с хорошим прилеганием (рис. 3.57, г). Простейшими профилями зубьев, обес­печивающими такой контакт, являются профили, очерченные по дуге окруж­ности или близкой к ней кривой.

б)

в) А - площадка контакта

Рис. 3.57. Передача с зацеплением М. Л. Новикова

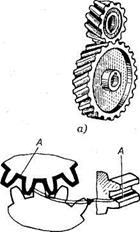
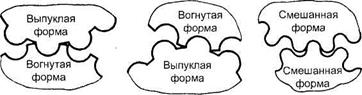
Обычно профиль зубьев шестерни делается выпуклым, а профиль зубь­ев колес вогнутым или наоборот (рис. 3.58, а, б), но могут быть передачи и с профилем зубьев шестерни и колеса, показанным на рис. 3.58, в. Такая конструкция зубьев увеличивает нагрузочную способность данной передачи по сравнению с эвольвентной передач

Ведущие шестерни

a) Ведомые колеса б) в)

Рис. 3.58. Профили зубьев в передачах с зацеплением М. Л. Новикова

при равных условиях. В зацеп­лении Новикова контакт зубьев теоретически осуществляется в точке, в эвольвентном зацеплении соприкосновение зубьев происходит по линии. Однако при одинаковых габаритных размерах передачи соприкосновение зубьев в зацеплении Новикова значительно лучше, чем соприкосновение в эвольвентном зацеплении.

Какие профили зубьев имеют распространенное применение в машино­строении? Основное конструктивное отличие зуба Новикова от известных.

3.83. Достоинства и недостатки передач с зацеплением Новикова. Высо­кая нагрузочная способность является основным достоинством передач с зацеплением Новикова. При твердости рабочих поверхностей до НВ 350 можно принимать допускаемую нагрузку примерно в 2,5 раза больше до­пускаемой нагрузки для эвольвентных прямозубых передач тех же основ­ных размеров, выполненных из тех же материалов, с той же термической обработкой (сравнение допускаемых нагрузок произведено при коэффици­енте нагрузки К= 1).

Благодаря большей нагрузочной способности передачи с зацеплением Новикова более компактны, имеют почти в 2 раза меньшие габариты по сравнению с передачами с эвольвентным зацеплением при одинаковой пе­редаваемой мощности.

Передачи с зацеплением Новикова допускают большее передаточное число, а вследствие хорошо удерживающейся масляной пленки между со­прикасающимися зубьями уменьшается изнашивание зубьев, повышается КПД передачи.

Потери на трение в зацеплении Новикова примерно в 2 раза меньше, чем потери в эвольвентном зацеплении. Шум во время их работы значи­тельно ниже.

Недостатками являются:

• большая (чем в эвольвентных зацеплениях) чувствительность к изме­нению межосевого расстояния;

• с увеличением нагрузки в зацеплении возрастает осевая составляю­щая, что, в свою очередь, усложняет конструкцию применяемых подшипниковых узлов;

• при ухудшении контакта (например, в случае перекоса валов и изме­нения межосевого расстояния) вся нагрузка, действующая на зубья, может сосредоточиться на небольшом участке длины зубьев, в ре­зультате чего зубья могут оказаться сильно перегруженными;

• необходимость иметь две специальные фрезы для нарезания зубьев (для шестерни и колеса).

Перечислите недостатки и основные достоинства зубчатых передач с за­цеплением Новикова и запишите в конспект.

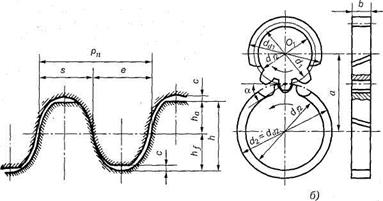
3.84. Стандартные исходные контуры для цилиндрической зубчатой пере­дачи с зацеплением Новикова для выпуклых (шестерня) и вогнутых (колесо) зубьев (рис. 3.59, а).

Основные геометрические размеры этих передач (рис. 3.59, б) опреде­ляют в зависимости от значения нормального модуля т_п (табл. 3.16 и 3.17).

а)

Рис. 3.59.Косозубая передача с зацеплением М. Л. Новикова

Таблица 3.16. Стандартные значения модулей для передачи с зацеплением Новикова

1-й ряд	2-й ряд	1-й ряд	2-й ряд	1-й ряд	2-й ряд
1,6		6,3
2,0	1,8		7,1
2,5	2,25			31,5	35,5
3,15	2,8	12,5	П,2
	3,55
	4,5
	5,6		22,4		i

Таблица 3.17. Геометрические параметры	передачи с зацеплением Новикова
Параметр, обозначение		Расчетные формулы
Нормальный модуль т„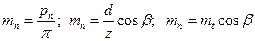
Торцовый модуль тt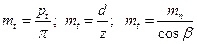
Диаметр вершин зубьев da		da = mt z + 1,8mn
Делительный диаметр d		d = mt z
Основной диаметр db		db = m,z cos α
Диаметр впадин зубьев df		d, = m,z - 2,1 т„
Нормальный шаг р„		р„ = πт„
Торцовый шаг рt		Pt = πmt
Осевой шаг рх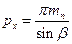
Окружная толщина зубьев 5		s = 1,53mn
Окружная ширина впадин зубьев е		e = 1,6mn
Высота зуба h		h = 1,95mn
Высота головки зуба ha		ha = 0,9mn

Окончание табл. 3.17

Параметр, обозначение	Расчетные формулы
Высота головки зуба hf	hf = 1,05mn
Радиальный зазор с	с = 0,15mn
Ширина венца b	b = kpx + ∆b
Межосевое расстояние аω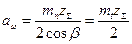

Примечание, β— угол наклона зубьев; β = 10 ÷ 30°; k — целое число осевых шагов р_х в ширине венца; ∆b — часть ширины венца больше целого числа осевых шагов (ширину венца рекомендуется выбирать с учетом выполнения условия b> 1,25р_x.); Z_∑ = Z\ + Z2 — суммарное число зубьев.

Запишите в конспект формулы для определения геометрических пара­метров передачи с

зацеплением Новикова (табл. 3.16). Выведите формулу ме­жосевого расстояния а, если известны d₂ и и, (u запишите ее в конспект).