Цилиндрические косозубые и шевронные зубчатые передачи. Устройство и основные геометрические и силовые соотношения
3.49. Косозубые зубчатые передачи, как и прямозубые, предназначены для передачи вращательного момента между параллельными валамя (рис. 3.36). У косозубых колес оси зубьев располагаются не по образующей делительного цилиндра, а по винтовой линии, составляющей с образующей угол β (рис. 3.44). Угол наклона зубьев р принимают равным 8÷18°, он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.
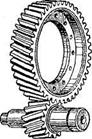
Рис. 3.36. Цилиндрическая косозубая передача
Передаточное число для одной пары колес может быть и ≤ 12. В прямозубых передачах линия контакта параллельна оси, а в косозубых расположена по диагонали на поверхности зуба (контакт в прямозубых передачах осуществляется вдоль всей длины зуба, а в косозубых — сначала в точке увеличивается до прямой, «диагонально» захватывающей зуб, и постепенно уменьшается до точки).
Достоинства косозубых передач по сравнению с прямозубыми: уменьшение шума при работе; меньшие габаритные размеры; высокая плавность зацепления; большая нагрузочная способность; значительно меньшие дополнительные динамические нагрузки.
За счет наклона зуба в зацеплении косо-зубой передачи появляется осевая сила.
Направление осевой силы зависит от направления вращения колеса (рис. 3.37), направления винтовой линии зуба, а также от того, каким является колесо — ведущим или ведомым. Осевая сила дополнительно нагружает валы и опоры, что является недостатком косозубых передач.
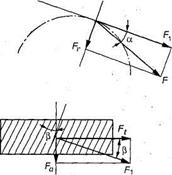
Рис. 3.37. Усилия в косозубой цилиндрической передаче
3.50.Шевронные зубчатые колеса представляют собой разновидность косозубых колес (рис. 3.38).
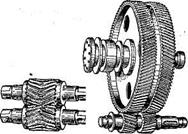
а) б)
Рис. 3.38. Шевронная зубчатая передача
Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями (рис. 3.38, а), называют шевронным колесом. Часть венца зубчатого колеса, в пределах которого линии зубьев имеют одно направление, называют полушевроном. Различают шевронные колеса с жестким углом (рис. 3.38, б), предназначенным для выхода режущего инструмента при нарезании зубьев. Шевронные передачи обладают всеми преимуществами косозубых, а осевые силы (рис. 3.39) противоположно направлены и на подшипник не передаются.
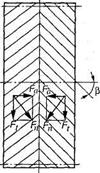
Рис. 3.39. Усилия в зацеплении шевронных зубчатых колес
В этих передачах допускают большой угол наклона зубьев (β = 25 ÷ 40°). Ввиду сложности изготовления шевронные передачи применяют реже, чем косозубые, т. е. в тех случаях, когда требуется передавать большую мощность и высо-кую скорость, а осевые нагрузки нежелательны.

Рис. 3.40
Будет ли возникать осевая сила в передаче, состоящей из зубчатых колес (рис. 3.40)? Чем отличается эта передача от косозубой?
3.51. Косозубые и шевронные колеса в отличие от прямозубых имеют два шага и два модуля: в нормальном сечении (см. рис. 3.44) по делительной окружности — нормальный шаг рп, в торцовой плоскости — торцовый шаг рt. Из условия, что модуль зацепления равен шагу, деленному на число π, имеем тп = р1/π; тt = рt /п.
Для косозубых и шевронных колес значения нормального модуля тn стандартизованы, так как профиль косого зуба в нормальном сечении соответствует исходному контуру инструментальной рейки и, следовательно, т = тп (косозубые и шевронные колеса нарезают, тем же способом и инструментом, что и прямозубые). Нормальный модуль тп является исходным при геометрических расчетах.
Определим зависимость между нормальным и торцовым шагом и модулех через угол наклона зубьев.
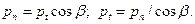
Если левую и правую части разделим на л, получим
mn = mt cosβ; mt = mn /cosβ.
3.52. Геометрические параметры цилиндрической косозубой и шевронной передач с эвольвентным профилем зуба рассчитают по формулам, приведенным в табл. 3.13. По торцовому модулю тt рассчитывают делительные (начальные) диаметры, а до тп — все остальные размеры зубчатых колес.
Таблица 3.13. Геометрические параметры цилиндрической косозубой передачи
| Параметр, обозначение | Расчетные формулы | |
| Нормальный модуль т„ | 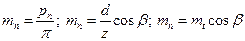 | |
| Торцовый (окружной модуль) тt | 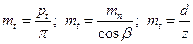 | |
| Диаметр вершин зубьев da | 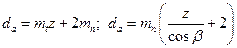 | |
| Делительный диаметр d | 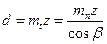 | |
| Диаметр впадин зубьев df | 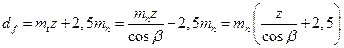 | |
| Шаг нормальный рn | 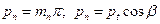 | |
| Шаг торцовый (окружной) рt | 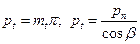 | |
| Окружная толщина зубьев St | 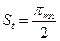 | |
| Ширина впадин зубьев et | 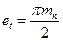 | |
| Параметр, обозначение | Расчетные формулы | |
| Высота зуба h | h = 2,25mn | |
| Высота головки зуба ha | ha = mn | |
| Высота ножки зуба hf | hf.=l,25mn | |
| Радиальный зазор с | с = 0,25mn | |
| Межосевое расстояние aω | 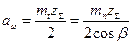 | |
| Длина зуба b | 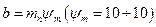 | |
| Ширина венца bω | 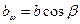 |
Окружная сила Ft= P/v. На косой зуб действует осевая сила Fa = Ft tgα (см. рис. 3.37), радиальная (распорная) сила Fr= Ft tga/cosβ.
Определите тп и mt, если известны делительный диаметр и межосевое расстояние.
3.53. В косозубдй передаче сила F, действующая на зуб косозубого колеса
(см. рис.3.44), направлена по нормали к профилю зуба, т. е. по линии зацепле
ния эквивалентного прямозубого колеса, и составляет угол а с касательной к
эллипсу.
Эту силу разложим на две составляющие: окружную силу на эквивалентном колесе Ft и радиальную (распорную) силу на этом колесе Fr.
Если, в свою очередь, силу F} разложить по двум направлениям, то получим такие силы: F, — окружную силу, Fa — осевую.
3.54. Для зубчатого колеса с шевронным зубом окружную силу F1 и рас
порную Fr определяют по тем же формулам, что и для косозубой передачи,
т. е. Ft= P/v, Fr= Ft tgα/cosβ. В шевронной передаче осевая сила Fa = 0 (см.
рис. 3.39).
Почему в шевронной передаче (см. рис. 3.38) осевая сила равна нулю?
3.55.Винтовая передача (разновидность косозубой) состоит из двух косозубых цилиндрических колес (рис. 3.42). Однако в отличие от косозубых цилиндрических передач с параллельными валами касания между зубьями здесь происходит в точке и при значительных скоростях скольжения. Поэтому при значительных нагрузках винтовые зубчатые передачи работать удовлетворительно не могут.
По рис. 3.42 определите, как расположены оси валов у винтовой передачи.
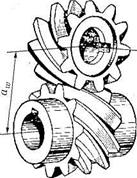
Рис. 3.41.Винтовая зубчатая передача
3.56. Ответить на вопросы контрольной карточки 3.8.
| Контрольная карточка 3.8 | ||
| Вопрос | Ответы | Код |
| Покажите на рис. 3.42 нормальный шаг зубьев р„ | Х1 Х2 Х3 Х4 На рисунке не показан | |
| В каких пределах принимают угол наклона зубьев (р) для косозубой зубчатой передачи? | 8 ÷ 18° 25 ÷ 45° 20° 90° | |
| Какой модуль принимают стандартным при расчете косозубой зубчатой передачи? | Тn тt Оба | |
| Укажите формулу для расчета передаточного числа косозубой передачи, если известны диаметры, показанные на рис. 3.43 | da/da da2/dax d/d2 d2/d\ | |
| По какому модулю рассчитывают делительный размер в косозубой передаче? | Тn my По обоим |
Рис. 3.42
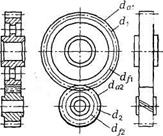
Рис. 3.43
