Расчёт термического сопротивления горизонтальной ограждающей конструкции

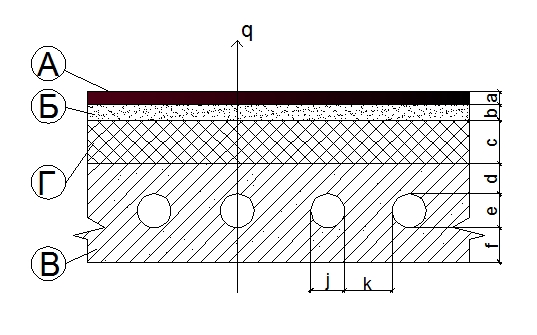
Рисунок 1.2 - Конструкция покрытия здани

А- рубероид

Б- гравий керамзитовый

В -железобетон

Г- маты минераловатные прошивные

Расчетные значения коэффициентов теплопроводности λ и теплоусвоения S материалов принимаем по таблице А.1[1] для условий эксплуатации ограждений «Б»:

- рубероид

λ ₁ = 0,17 Вт/( м ∙°С); S₁ = 3,53Вт/(м² ∙°С);

- гравий керамзитовый

λ ₂ = 0,2 Вт/( м ∙°С); S₂ = 2,91 Вт/(м² ∙°С);

- маты минераловатные прошивные

λ₃ = 0,048 Вт/( м ∙°С); S₄ = 0,57 Вт/(м² ∙°С);

- железобетон

λ₄ = 2,04 Вт/( м ∙°С); S₅ = 19,7Вт/(м² ∙°С).

Конструктивное решение представлено на рисунке 1.2. Предварительно, для нахождения термического сопротивления перекрытия определили толщину искомого слоя Х. Для этого по таблице 5.1[1] выбираем нормативное сопротивление теплопередачи R_т^норм=6 (м²· ⁰С)/Вт. Сопротивление искомого слоя находим по формуле:

R₃= R_т^норм–( ;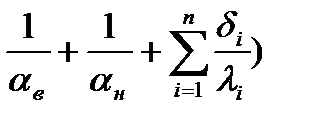

где α_в-коэффициент теплоотдачи внутренней поверхности ограждающей конструкции,(1,таблица 5.4)

α_н-коэффициент теплоотдачи наружной поверхности ограждающей конструкции для зимних условий, принимаем по таблице 5.7[1].

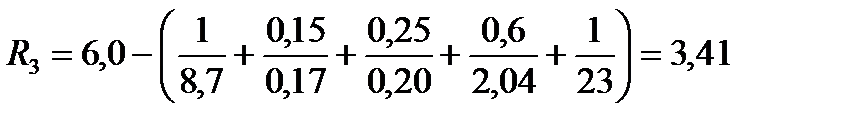
Определяем толщину искомого слоя:

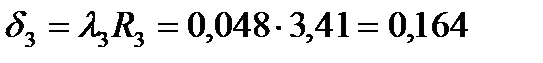
Разделим конструкцию на повторяющиеся элементы, приняв, что данный элемент имеет правильную геометрическую форму прямоугольника со сторонами 0,1х0,1 м???.

Определим термическое сопротивление элементов при условии деления их плоскостями, параллельными тепловому потоку. Конструктивное решение представлено на рисунке 1.2.1. Плоскости где?

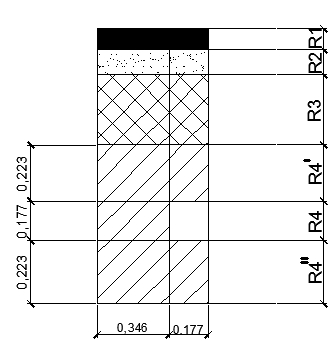
Рисунок1.2.1(1) Элемент перекрытия

Здесь обрезаем по границе квадрата

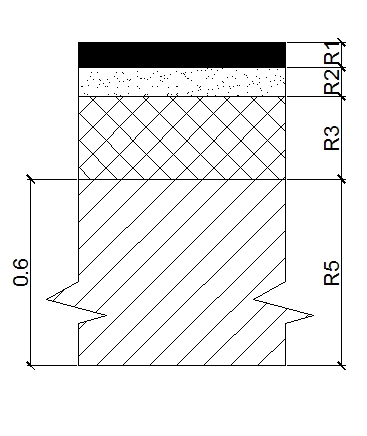
Рисунок1.2.1(2) Элемент перекрытия

Здесь даем в размер 0,346, никаких обрезков

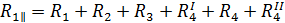
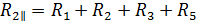
Где Ri – термическое сопротивление каждого слоя конструкции, (м²∙°С)/Вт.

Железобетонную плиту разбиваем на три слоя: два слоя железобетона и слой воздушной прослойки. Неверно пересчитана толщина бетона

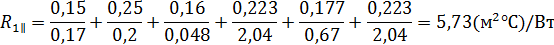
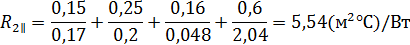
Коэффициент теплопроводности замкнутой воздушной прослойки при толщине 0,089 (м), что примерно равно 0,1 (м) примем λ = 0,67(м²∙°С)/Вт.

Определяем площади элементов:

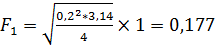м²;

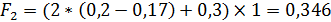м²; И здесь лишнего насчитал

Термическое сопротивление элемента при условии деления его плоскостями,

параллельными тепловому потоку.

;

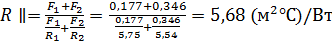Находим термическое сопротивление при условном делении его плоскостями, перпендикулярными тепловому потоку. Конструктивное решение представлено на рисунке 1.2.2. Где плоскости?

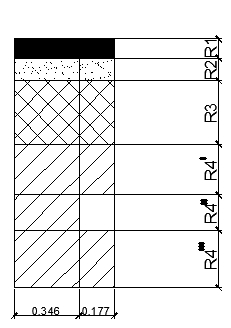
Рисунок 1.2.2 Конструкция перекрытия при условии деления его плоскостями, перпендикулярными тепловому потоку

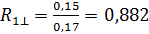(м²· ⁰С)/Вт;

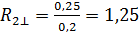(м²· ⁰С)/Вт;

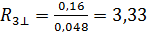(м²· ⁰С)/Вт;

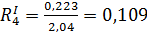(м²· ⁰С)/Вт;

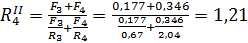(м²· ⁰С)/Вт;

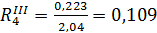(м²· ⁰С)/Вт;

Тогда,

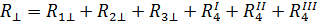
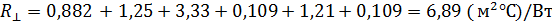
Так как величина 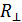не превышает величину R_││более чем на 25%, в нашем случае это составляет 17,5 %, то термический расчет конструкции выполняют согласно формуле:

R_ка= 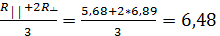(м²· ⁰С)/Вт ;

Вывод: данная конструкция перекрытия удовлетворяет требованиям [1] по теплопроводности, так как нормативное сопротивление конструкции

R^норм= 6,0(м²∙°С)/Вт., что меньше расчетного сопротивления R=6.48(м²∙°С)/Вт.