Работа и КПД на окружности двухвенечного колеса скорости
Расчет работы на окружности для колес со ступенями скорости, как и для одноступенчатой ступени, производится двумя путями:
4. По балансу располагаемой энергии и потерь
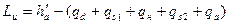 , (4.2.1)
, (4.2.1)
где учтены потери в соплах qd, потери в первом ряду рабочих лопаток qs1, потери в венце направляющих лопаток qн, потери во втором ряду рабочих лопаток qs2 и потери с выходной скоростью qa.
5. По элементам треугольников скоростей
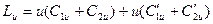 (4.2.2)
(4.2.2)
Или
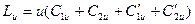 (4.2.3)
(4.2.3)
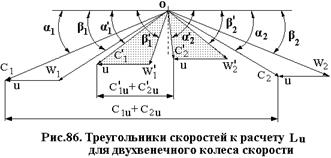 При этом окружные составляющие скоростей C1u и C2u,
При этом окружные составляющие скоростей C1u и C2u, 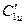 и
и 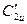 непосредственно снимаются с треугольников скоростей (рис.86).
непосредственно снимаются с треугольников скоростей (рис.86).
 Коэффициент полезного действия на окружности определяется отношением работы на окружности Lu к адиабатному теплоперепаду ha
Коэффициент полезного действия на окружности определяется отношением работы на окружности Lu к адиабатному теплоперепаду ha

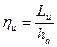 (4.2.4)
(4.2.4)
Значение работы на окружности Lu можно показать на диаграмме h-s (рис.84 и 85).
В общем случае кроме потерь на окружности могут наблюдаться и другие внутренние потери:
7. Потери, связанные с протечками пара через зазоры qз.
8. Потери, связанные с парциальным подводом пара qв.
9. Потери на трение о пар диска и бандажа qr.
10. Потери, связанные с влажностью пара qх.
11. Неучтенные потери qн.
Определив все внутренние потери в двухвенечном колесе скорости, можно записать выражение для внутренней работы (удельной внутренней работы, производимой 1 кг/пара)
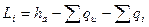 (4.2.5)
(4.2.5)
где 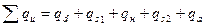 - сумма потерь энергии на окружности;
- сумма потерь энергии на окружности;
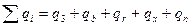 - сумма внутренних потерь, без учета
- сумма внутренних потерь, без учета 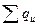 .
.
Внутренний КПД турбинной ступени 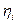 - это отношение внутренней работы к адиабатному теплоперепаду на колесе
- это отношение внутренней работы к адиабатному теплоперепаду на колесе
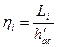 (4.2.6)
(4.2.6)
Отложив вверх 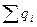 от точки Аа, найдем энтальпию h1 и точку А1, определяющую состояние пара за двухвенечным колесом скорости на диаграмме h-s (рис.84 и 85).
от точки Аа, найдем энтальпию h1 и точку А1, определяющую состояние пара за двухвенечным колесом скорости на диаграмме h-s (рис.84 и 85).
Далее исследуем зависимость КПД на окружности двухвенечного колеса (колеса с двумя ступнями скорости) от отношения скоростей ξ.
С целью упрощения выкладок введем ряд допущений, которые не повлияют на качественный характер искомой зависимости:
1) Примем, что степень реакции ступни ρ = 0, т.е. ступень является чисто активной.
2) Пренебрежем всеми потерями энергии, кроме выходной потери qa. Тогда
φ=1, q=0, т.е. С1=С1t;
ψs1=1, q s1=0, т.е. W2=W1;
ψн=1, qн =0, т.е. 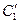 = С2; (4.2.7)
= С2; (4.2.7)
ψs2=1, qs2=0, т.е. 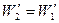 ,
,
где индекс «н» означает, что рассматриваемые параметры относятся к направляющему венцу, а индексы «s1» и «s2» указывают на первый и второй ряды рабочих лопаток.
3) Считаем, что лопатки рабочих и направляющих венцов симметричны, т.е.

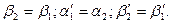 (4.2.8)
(4.2.8)
 При сделанных допущениях треугольники скоростей примут вид, показанный на рис.87 (выходные треугольники повернуты на 180о относительно вертикальной оси, проходящей через полюс 0).
При сделанных допущениях треугольники скоростей примут вид, показанный на рис.87 (выходные треугольники повернуты на 180о относительно вертикальной оси, проходящей через полюс 0).
Используя выражение (2.4.6), где работа на окружности Lu двухвенечного колеса равна сумме работ на окружности каждого из венцов
 Lu=Lu1+Lu2, (4.2.9)
Lu=Lu1+Lu2, (4.2.9)
а адиабатный теплоперепад в соответствии с принятыми допущениями определяется выражением


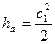 , (4.2.10)
, (4.2.10)
опуская промежуточные выкладки и учитывая (4.2.7), (4.2.8), (4.2.9) и (4.2.10), окончательно получим:
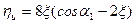 , (4.2.11)
, (4.2.11)
где, как и ранее,
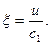 (4.2.12)
(4.2.12)
Из выражения (4.2.11) следует, что ηu = 0 при ξ = 0 и
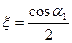 . (4.2.13)
. (4.2.13)
Оптимальное значение отношения скоростей
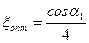 . (4.2.14)
. (4.2.14)
График функции ηu = ƒ(ξ) в случае двухвенечного колеса (z=2) показан на рис. 88.
В общем случае для активного колеса (p=0), имеющего z ступеней скорости, оптимальное отношение скоростей равно 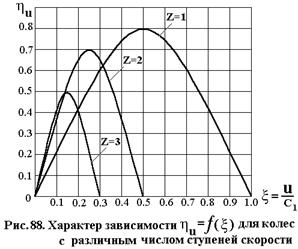
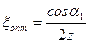 . (4.2.15)
. (4.2.15)
Если принять, что 
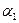 – малый угол и соs
– малый угол и соs 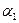
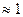 , то согласно (4.2.15), получим:
, то согласно (4.2.15), получим:
для одновенечного колеса (z=1) 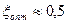 ;
;
для двухвенечного колеса (z=2) 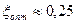 ;
;
для трехвенечного колеса (z=3) 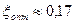 и т.д.
и т.д.
Для колес со ступенями скорости, у которых ρ>0 имеющих z ступеней, оптимальное отношение скоростей равно
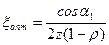 . (4.2.16)
. (4.2.16)
Для суждения об абсолютной величине КПД на окружности двухвенечного колеса формула (4.2.11) оказывается непригодной, так как при выводе этой формулы мы пренебрегли всеми потерями. Представим поэтому формулу для КПД на окружности в таком виде:
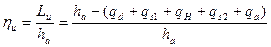 , (4.2.17)
, (4.2.17)
где учтены потери в соплах qd, потери в первом ряду рабочих лопаток qs1, потери в венце направляющих лопаток qн, потери во втором ряду рабочих лопаток qs2 и потери с выходной скоростью qa.
Для одновенечной ступени КПД на окружности составляет
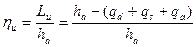 . (4.2.18)
. (4.2.18)
Из сравнения выражений (4.2.17) и (4.2.18) видно, что даже если принять на оптимальном режиме потери qd, qs1 и qа для одновенечного и двухвенечного колес одинаковыми, то КПД двухвенечного колеса окажется ниже из-за дополнительных потерь qн и qs2. Таким образом, с увеличением числа ступеней максимально достижимый КПД уменьшается. На рис.88 показан характер зависимости ηu=ƒ(ξ) для колес с различным числом ступеней скорости.
Обычно максимальный КПД на окружности имеет следующий порядок:
для одновенечного колеса (z = 1): 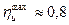 ;
;
для двухвенечного колеса (z = 2): 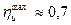 ;
;
для трехвенечного колеса (z = 3): 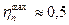 .
.
Итак, мы установили, что максимальный КПД двухвенечного колеса существенно ниже, чем КПД одновенечной ступени. Возникает вопрос о целесообразности применения двухвенечных колес. Здесь, однако, следует подчеркнуть, что преимуществом двухвенечного колеса является его способность сработать большой теплоперепад при ограниченной окружной скорости и. Так, принимая, что сравниваемые одновенечное и двухвенечное колеса работают при одинаковых окружных скоростях и, а также при оптимальных для каждой ступени отношениях скоростей, получим при 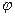 = 1:
= 1:
а) в случае одновенечной ступени (z = 1):
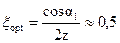 ,
,
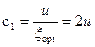 , (4.2.19)
, (4.2.19)
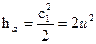 ;
;
б) в случае двухвенечной ступени (z = 2):
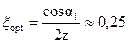 ,
,
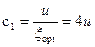 , (4.2.20)
, (4.2.20)
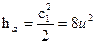 .
.
Сравнивая (4.2.19) и (4.2.20), видим, что при названных условиях двухвенечное колесо может сработать теплоперепад в 4 раза больше, чем одновенечная ступень, т.е.
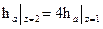 . (4.2.21)
. (4.2.21)
Таким образом, для того, чтобы сработать теплоперепад, характерный для двухвенечного колеса, пришлось бы установить четыре одновенечные ступени, что намного увеличило бы осевые размеры и вес турбины.
