Расчет рыбообразных стрел
Расчетная схема разнообразной стрелы с дополнительными подвесками приведена на рис. 154 ([3], стр.237). Стрела представляет собой многоопорную неразрезную балку, подвешенную при помощи независимых подвесок и двуногой или дополнительной стойке. Ковш экскаватора под действием подъемных и тяговых канатов может находиться в любой точке под стрелой.
Исследования показали, что за расчетные случаи нагружения стрелы следует принимать следующие два положения ковша с грунтом: наибольший вылет при вертикальном положении подъемных канатов и подъем груженного ковша на выгрузку при минимальном угле между канатами подъема и осью стрелы. Таким образом, равнодействующая от канатов подъема имеет два значения и направления RnI и RnII.
На стрелу действуют следующие нагрузки:
RnI, RnII – равнодействующая расчетных усилий в канатах подъема в двух расчетных положениях; qстр – распределенный вес стрелы; Gб – вес блоков головы стрелы и головной части стрелы; Рк – горизонтальная инерционная нагрузка от ковша с грунтом, возникающая при повороте экскаватора; qе – распределенная горизонтальная инерционная нагрузка от собственного веса стрелы; Рσ – горизонтальная инерционная нагрузка от веса блоков головы стрелы и головной части стрелы. Угол наклона α стрелы к горизонту имеет обычно постоянное значение.
Расчетная схема стрелы с двумя дополнительными подвесками при действии вертикальных и горизонтальных нагрузок показана на рис. 154, а ([3], стр.237).
Подбор сечений элементов подвески стрелы производят по усилиям в них Т1, Т2 и Т3. По усилиям в подвеске стрелы подбирают их натяжения при монтаже (при независимых подвесках) или кратность полистпастов (при зависимых подвесках).
При зависимых подвесках усилия Т1, Т2 и Т3 необходимо подбирать таким образом, чтобы соотношения между ними составляли четные числа – кратности полиспаста. Для достижения этого приходится варьировать длину пролетов l1, l2 и l3, а также высоту и наклон дополнительной стойки.
Проверяют общую устойчивость стрелы в вертикальной и горизонтальной плоскостях. Потеря общей устойчивости стрелы в вертикальной плоскости может произойти при ее выпучивании вверх. В этом случае промежуточные опоры от дополнительных подвесок не будет работать.
Проверяют общую устойчивость и подбирают элементы стрелы аналогично крановым решетчатым стрелам.
Расчет разнообразных стрел без дополнительных подвесок не отличается от расчета крановых стрел с прямолинейной осью.
Расчет трехгранных стрел
Действуют следующие нагрузки: RnI и RnII – равнодействующие расчетных усилий в канатах подъема в двух расчетных положениях; Gi – вес стрелы, приходящийся на i-ый узел стрелы; Рк – горизонтальная инерционная нагрузка от ковша с грунтом, возникающая при повороте экскаватора; Рi – горизонтальная инерционная нагрузка в i-том узле стрелы от веса Gi. Схемы действия вертикальных и горизонтальных нагрузок в стреле приведены на рис. 155 ([3], стр.241). Расчет пространственной стрелы следует свести к расчету плоских ферм: двух наклонных (по боковым граням) и одной горизонтальной (по нижней грани). С этой целью нагрузки раскладывают на эти грани также, как это делалось при расчете трехгранной стрелы крана. Расчетная схема боковой грани стрелы при действии инерционных нагрузок от собственного веса стрелы и веса ковша с грунтом показана на рис. 156, а ([3], стр.242), а горизонтальной грани – на рис.156, б ([3], стр.242). Верхний пояс стрелы воспринимает нагрузку от веса стрелы, как от правой, так и от левой наклонных ферм, т.е. усилия от нагрузок, найденных решением схемы (рис. 156, а, [3], стр.242), удваиваются. Нагрузка в поясах горизонтальной фермы от собственного веса стрелы и инерционных нагрузок складывается из усилий в наклонной ферме и горизонтальной ферме. Усилия в раскосах и стойках наклонных и горизонтальной фермы определяют по схемам (рис. 156, [3], стр.242). Гибкость сжатых поясов рекомендуется назначать не выше 80, растянутых – не выше 120, гибкость раскосов и стоек должна находиться в пределах 120…150.
Расчет вантовых стрел
Стрела состоит из трех вантовых ферм (рис. 153, а, [3], стр.235): одной вертикальной и двух наклонных, имеющих общий трубчатый пояс. Вантам наклонных ферм придается предварительное натяжение. Ввиду того, что центральный пояс состоит из трубы большего диаметра, в расчете необходимо учитывать жесткость нижнего пояса.
Высоту фермы стрелы подбирают из условия наивыгоднейшего использования прочности канатов вертикальной фермы. Высота составляет для первой от головы стрелы стойки (0,12…0,13)l, а для главной стойки (0,23…0,25)l. Ширина стрелы В в пятах ограничивается габаритами поворотной платформы экскаватора и принимается равной ее ширине. На стрелу действуют следующие нагрузки (рис. 157, [3], стр.244): RnI и RnII – равнодействующие усилий от веса ковша с грунтом в I или II расчетном положениях; Gi – собственный вес стрелы, приложенный к узлам стрелы; Рк – горизонтальная инерционная нагрузка от веса ковша с грунтом; Рi – горизонтальные инерционные нагрузки от собственного веса стрелы; N1, N2 и N3 – усилия от предварительного натяжения вант наклонных ферм; N4 и N5 – усилия от предварительного натяжения перекрестных вант нижних поясов; N6 и N7 – усилия от предварительного натяжения перекрестных вант задних подкосов. Расчетная схема стрелы от весовых нагрузок представляет собой статически определимую ферму, показанную на рис. 158, а ([3], стр.244). Усилия в элементах от собственного веса определяют любым известным способом. Элемент, соответствующий вантам, испытывающим усилие N5 в расчетной схеме отсутствует, так как влияние от предварительного натяжения вант усилием N5 и N6 распространяется только на элементы, смежные с этими вантами.
Основная система стрелы при воздействии переменных нагрузок RnI или RnII приведена на рис.158, б([3], стр.244). Эта система является трижды статически неопределимой и решается методом сил. Для определения действительных значений неизвестных сил определяем усилия в элементах стрелы от RnI и RnII, а также усилия от 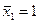 ;
; 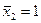 ;
; 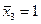 . Усилия от RnI или RnII целесообразно определять построением диаграммы Кремоны. Усилия в стержнях от неизвестных сил в наклонных фермах стрелы целесообразно определять по схемам, показанным на рис. 159, б ([3], стр.246).
. Усилия от RnI или RnII целесообразно определять построением диаграммы Кремоны. Усилия в стержнях от неизвестных сил в наклонных фермах стрелы целесообразно определять по схемам, показанным на рис. 159, б ([3], стр.246).
Расчетная схема нижнего пояса стрелы в вертикальной плоскости приведена на рис.163, а ([3], стр.249). На этой схеме q1– q5 – равномерно распределенные нагрузки собственного веса нижнего пояса стрелы и веса лестниц стрелы в соответствующих панелях; J1 ÷ J5 моменты инерции нижнего пояса стрелы в соответствующих панелях. Систему следует рассматривать как многоопорную неразрезную балку, которую необходимо решать методом последовательных приближений. Эпюра 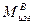 моментов от собственного веса нижнего пояса стрелы (рис.163, б [3], стр.249) представляет собой сумму эпюр пролетных и опорных моментов:
моментов от собственного веса нижнего пояса стрелы (рис.163, б [3], стр.249) представляет собой сумму эпюр пролетных и опорных моментов: 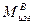 = Моп + Мпр. Для определения изгибающих моментов от горизонтального прогиба стрелы расчетную систему нижнего корпуса стрелы в боковой плоскости следует представлять как многоопорную балку переменной жесткости с моментами инерции Ji сечения в пролетах и длинами панелей li (рис.163, в [3], стр.249). После этого легко построить эпюру изгибающих моментов
= Моп + Мпр. Для определения изгибающих моментов от горизонтального прогиба стрелы расчетную систему нижнего корпуса стрелы в боковой плоскости следует представлять как многоопорную балку переменной жесткости с моментами инерции Ji сечения в пролетах и длинами панелей li (рис.163, в [3], стр.249). После этого легко построить эпюру изгибающих моментов 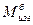 в боковой плоскости (рис.163, г [3], стр.249). Суммарная эпюра моментов Мизг, определяемая по зависимости Мизг =
в боковой плоскости (рис.163, г [3], стр.249). Суммарная эпюра моментов Мизг, определяемая по зависимости Мизг = 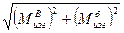 , представлена на рис.163, д ([3], стр.249).
, представлена на рис.163, д ([3], стр.249).
Литература:
Основная: 3 [разд.9: с.180÷214; разд.10: с.215÷255]
Контрольные вопросы.
1. Какие нагрузки действуют на стрелу прямой лопаты, приведите расчетную схему для проверки напряжений в верхней части стрелы экскаватора и в каком случае возникают максимальные напряжения в сечениях верхней части стрелы (выше напорного вала)?
2. Напишите формулу для определения суммарного изгибающего момента в расчетном сечении стрелы в вертикальной плоскости и для каких расчетных положений определяются реактивные усилия R, V и Pб в пятах стрелы?
3. Из скольких возможных положений рукояти следует определять напряженное состояние в наиболее опасных сечениях рукояти, приведите и объясните эти расчетные положения, а также в каком случае возникает наибольшее напряженное состояние в сечениях балки рукояти, приведите расчетную схему с действующими нагрузками?
4. Когда возникают наибольшие нагрузки в балке стрелы и приведите действующие нагрузки в расчетной схеме и как производится расчет стрелы с изменением вылета при помощи подвижной каретки?
5. Приведите геометрические параметры стрел с учетом назначения генеральных размеров фермы стрелы с прямолинейной осью, а также для стрел, работающих на изгиб?
6. Как производится расчет башен кранов, трехгранных, рыбообразных и вантовых стрел?
