Определение скорости выхода пара из каналов рабочей решетки
Теперь рассмотрим течение пара в рабочей решетке. Поскольку рабочие лопатки вращаются, нам необходимо рассматривать относительное движение пара. 
Пусть скорость пара на входе в рабочую решетку равна W1 (рис.13), а состояние пара характеризуется точкой Аd диаграммы h-s, т.е. давление и температура пара соответственно равны Рd и td. Пар на входе в решетку обладает кинетической энергией  . Отложив энергию
. Отложив энергию  вверх от точки Аd, найдем точку Аd, характеризующую параметры торможения потока.
вверх от точки Аd, найдем точку Аd, характеризующую параметры торможения потока.
Вначале пренебрегаем трением и другими сопротивлениями решетки, т.е. рассматриваем «теоретический» процесс.
 Если решетка реактивная (рис.13), то давление за решеткой Р1 меньше давления Рd. Проведя из точки Аd адиабату до пересечения с изобарой Р1, можно найти точку Аst, определяющую состояние пара в конце «теоретического» процесса и снять в этой точке энтальпию hst.
Если решетка реактивная (рис.13), то давление за решеткой Р1 меньше давления Рd. Проведя из точки Аd адиабату до пересечения с изобарой Р1, можно найти точку Аst, определяющую состояние пара в конце «теоретического» процесса и снять в этой точке энтальпию hst.
Если же решетка активная(рис.14), то давление Рd и Р1 одинаковы. В этом случае при «теоретическом» процессе течения состояние пара не изменяется, т.е. точка Аst совпадает с точкой Аd, а энтальпия hst равна энтальпии hd.
Теперь обозначим через W2t теоретическую скорость выхода пара из решетки и перейдем к записи уравнения энергии. При этом следует иметь в виду, что на рассматриваем относительное движение пара, т.е. выбранная система координат вращается вместе с рабочими лопатками с угловой скоростью ω. Поэтому для общего случая уравнение энергии должно быть записано в следующем виде:
 (3.15)
(3.15)
где Lf – работа сил обусловленных вращением системы координат, при перемещении массы пара от входного до выходного сечений решетки.
При вращении рабочего тела вместе с координатными осями на него действуют центробежная и кориолисова силы. Поэтому Lf– это работа центробежной и кориолисовой сил. Но при установившемся движении траектории частиц пара совпадают с линиями тока и поэтому работа кориолисовой силы, направленной нормально к вектору относительной скорости W при относительном движении равна нулю.
Кроме того, заметим, что согласно гипотезы плоских сечений, радиальные перемещения частиц пара отсутствуют – общее направление движения пара совпадает с направлением оси турбины (такие турбины называют осевыми). Поэтому для рассматриваемого случая работа центробежной силы, которая направлена по радиусу, также равна нулю.
Таким образом, для установившегося движения пара в осевой турбины можно положить Lf=0 и записать уравнение энергии (2.2.15) в виде:
 (3.16)
(3.16)
Разность энтальпий на входном и выходном сечениях решетки обозначается has и называется адиабатным теплоперепадом на рабочих лопатках:
has=hd-hst (3.17)
Тогда из (2.2.16) получим выражение для теоретической скорости истечения пара:
 (3.18)
(3.18)
Введем понятие располагаемого адиабатного теплоперепада на рабочих лопатках:
 (3.19)
(3.19)
Тогда формула (2.2.18) будет иметь вид:
 (3.20)
(3.20)
Теперь обратимся к реальному потоку, в котором действуют силы вязкости. Действительная скорость выхода пара из рабочих лопаток W2, будет несколько меньше. Различие между действительной и теоретической скоростью характеризуется коэффициентом скорости, который применительно к рабочим лопаткам обозначается через ψ:
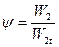 (3.21)
(3.21)
Коэффициент скорости ψ определяется опытным путем и обычно его величина имеет порядок 0.9÷0.95.
Таким образом, определения скорости выхода пара из рабочих лопаток получим формулы:
 (3.22)
(3.22)
или
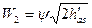 (3.23)
(3.23)
Формулы (2.2.22) и (2.2.23) имеют общий характер, т.е. применимы как для реактивных, так и для активных лопаток. Но для активных лопаток has=0. Поэтому в частном случае, для активной рабочей решетки, получим:
W2=ψW1 (3.24)
Определим состояние пара за рабочими решетками. По аналогии с направляющим аппаратом определим потери кинетической энергии на рабочих лопатках как разность между располагаемой и действительной кинетической энергией:
 (3.25)
(3.25)
Тогда коэффициент потерь ςs, определяемый отношением потерянной кинетической энергии к располагаемой кинетической энергии, будет равен:
 (3.26)
(3.26)
Для вычисления потерь qs получим формулы:
 (2.2.27)
(2.2.27)
или
 (3.28)
(3.28)
В частном случае, для активной рабочей решетки, можно записать:
 (3.29)
(3.29)
Потерянная кинетическая энергия qs расходуется на преодоление трения и прочих сопротивлений, что приводит к росту энтальпии пара. Поэтому действительная энтальпия пара за рабочими лопатками будет равна:
hs=hst+qs(3.30)
На диаграмме h-s (рис.13 и 14) энтальпия hs легко находится, отложив потерю qs вверх от точки Аst (или от точки Аd для активной решетки). Точка Аs, определяющая действительное состояние пара за рабочими лопатками, определится пресечением изобары Р1 (или Рd для активной решетки) и линии постоянной энтальпии hs=const.
Зная начальное (точка Аd) и конечное (точка Аs) состояние пара на диаграмме h-s можно провести линию, характеризующую действительный процесс течения пара в рабочей решетке. Для реактивной решетки (рис.13)
