Аналитические методы определения усилий
При использовании этих методов предварительно определяют опорные реакции. Затем рассматриваемую часть фермы отделяют разрезом от остальной части фермы, действие которой на рассматриваемую часть заменяется внутренними усилиями, возникающими в разрезанных стержнях. Для определения усилий составляют основные уравнения равновесия статики.
Метод вырезания узлов. При этом методе рассмотрения фермы начинают с такого узла, в котором сходятся не более двух стержней, т.е. с опорных узлов, на которые действуют определенные реакции. Имеем ферму (рис. 18, а) на которую действуют неподвижные внешние силы Q1, Q2 и Q3. Вырежем узел 1 на опоре А.
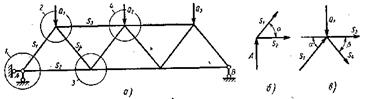
Рисунок 18-Определение усилий методом вырезания узлов.
В этом узле (рис.18,б) действуют по величине и направлению реакция А и усилия в стрежнях S1 и S2. Знаки усилий неизвестны, и при составлении уравнений равновесия примем усилия растягивающими, т.е. направим их от узла 1 (рис. 18,б).
Уравнения равновесия для узла 1
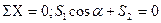 (29)
(29)
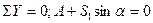 (30)
(30)
отсюда
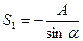 и
и 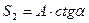 (31)
(31)
Знак минус у усилия S1 показывает, что стержень на самом деле сжат, а не растянут, как это было принято при составлении уравнений.
Затем рассматривают узел 2, в котором действуют известные по величине и направлению силы Q1 и S1 (рис. 18, в) и неизвестные силы S3 и S4, которые опять предполагаем растягивающими стержнями.
Уравнение равновесия для узла 2
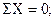
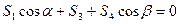 (32)
(32)
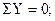
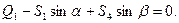 (33)
(33)
Решая эти два уравнения, определяем величину и знак усилий S3 и S4.
Далее последовательно рассматривают узлы 3,4 и т.д., пока не будут определены усилия во всех стержнях фермы.
Метод сечений (метод Риттера) позволяет сразу найти усилие в любом рассматриваемом стержне без предварительного определения усилий в предыдущих стержнях. Рассмотрим этот метод на общем случае фермы с непараллельными поясами (рис. 19).
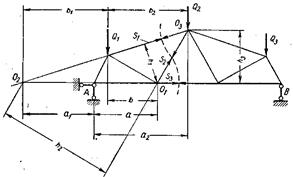
Рисунок 19 – Определение усилий методом сечений
Для определения усилий S1, S2 и S3 проводится разрез фермы через эти стержни. Так как знак усилий неизвестен, то предполагаем стержни растянутыми и направляем усилия стрелками к отсеченной части фермы. Составим уравнение относительно точки О1 (точки Риттера), в которой пересекаются два из трех рассматриваемых стержней:
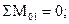
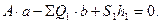 (34)
(34)
В этом уравнении 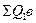 - сумма произведений всех внешних сил, действующих на рассматриваемую часть фермы, на плечо этих сил относительно точки Риттера О1.
- сумма произведений всех внешних сил, действующих на рассматриваемую часть фермы, на плечо этих сил относительно точки Риттера О1.
отсюда
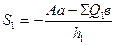 (35)
(35)
Знак минус показывает, что на самом деле стержень будет не растянуть, а сжат.
Для определения усилия S2 в стержне необходимо принять за точку Риттера точку О2, находящуюся на пересечении линий действий усилий S1 и S2. Уравнения моментов усилий относительно этой точки
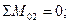
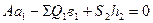 (36)
(36)
отсюда
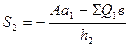 (37)
(37)
Для определения усилия S3 за точку Риттера принимаем точку О3, в которой пересекаются линии действия усилий S1 и S2. Тогда
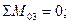
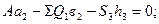 (38)
(38)
отсюда
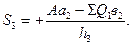 (39)
(39)
В тех случаях, когда пояса фермы параллельны и точка Риттера О2 находится в бесконечности (рис. 20), усилие S2 в раскосе (сечение 1-1), а также усилие S4 в стойке (сечение 2-2) определяют составлением уравнения проекций на вертикаль всех сил, действующих на одну из частей фермы.
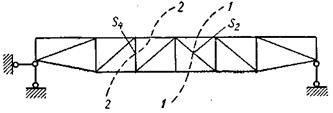
Рисунок 20 – Определение усилий при параллельных поясах
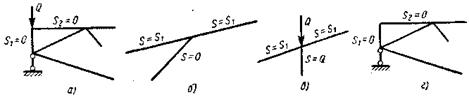
Рисунок 21 – Схемы к определению усилий методом сечений.
При применении способа Риттера необходимо учитывать следующее:
1. Если узел фермы образован из двух стержней и внешнее усилие направлено вдоль одного из них, то усилие в этом стержне равно внешней нагрузке, а в другом стержне усилие равно нулю (рис. 21, а)
2. Если в узле фермы сходятся три стержня, из которых два направлены по одной прямой, и к этому узлу не приложена внешняя нагрузка, то в стержнях, лежащих на одной прямой усилия равны между собой, а в третьем стержне усилие равно нулю (рис. 21,б).
3. Если в узле фермы сходятся три стержня, из которых два направлены по одной прямой, и к узлу приложена внешняя нагрузка, действующая по направлению третьего стержня, то усилия в стержнях, лежащих на одной прямой, равны между собой, а в третьем стержне усилие равно приложенной внешней нагрузке (рис. 21, в).
4. Если в узле фермы сходятся два пересекающихся стержня и к узлу нагрузка не приложена, то усилие в каждом стержне равно нулю (рис. 21, г).
