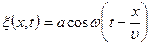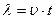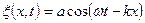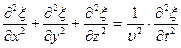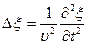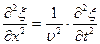Волновое уравнение и его решение

МЕХАНИЧЕСКИЕ ВОЛНЫ

План.

1. Механизм образования механических волн в упругой среде. Продольные и поперечные волны. Волновое уравнение и его решение. Гармонические волны и их характеристики.

2. Фазовая скорость и дисперсия волн. Волновой пакет и групповая скорость.

3. Понятие о когерентности. Интерференция волн. Стоячие волны.

4. Эффект Доплера для звуковых волн.

1. Механизм образования механических волн в упругой среде.

Если в каком-либо месте упругой среды (твердой, жидкой или газообразной) возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью. Процесс распространения колебаний в пространстве называется волной. Геометрическое место точек, до которых доходят колебания к моменту времени t называется фронтом волны (волновым фронтом). В зависимости от формы фронта волна может быть сферической, плоской и др.

Волна называется продольной, если направление смещения частиц среды совпадает с направлением распространения волны.

Продольная волна распространяется в твердых, жидких и газообразных средах.

Волна называется поперечной, если смещение частиц среды перпендикулярно направлению распространения волны. Поперечная механическая волна распространяется только в твердых телах (в средах обладающих сопротивлением сдвигу, поэтому в жидкостях и газах такая волна распространиться не может).

Волновое уравнение и его решение.

Уравнение, позволяющее определить смещение 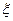(х,t) любой точки среды с координатой х в любой момент времени t называется уравнением волны.

Например, уравнение плоской волны, т.е. волны, распространяющейся в одном направлении, например в направлении оси х, имеет вид

(28-1)

,

где 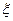(х,t) – смещение точек через время t, за которое волна распространяется на расстояние х = 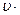t ( 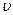- скорость распространения волны).

Расстояние 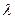, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны

Введем величину 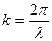, которая называется волновым числом.

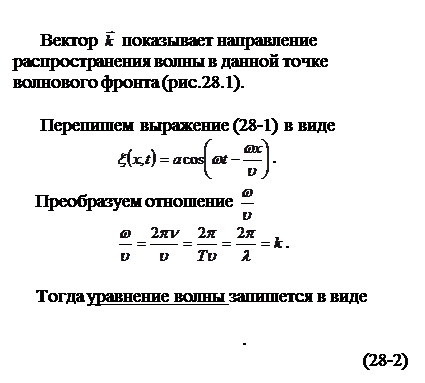Если умножить волновое число на единичный вектор направления распространения волны 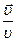, то получится вектор, называемый волновым вектором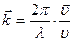

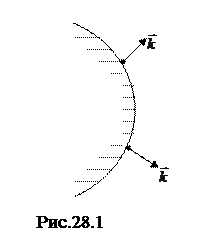На рис.28.2 представлено графическое изображение волны

Уравнение любой волны является решением дифференциального уравнения, называемого волновым уравнением

С помощью оператора Лапласа 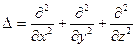(лапласиана) это уравнение можно записать более кратко

В случае плоской волны волновое уравнение

(Решением этого уравнения является уравнение волны (28-1), (28-2).)

2. Фазовая скорость и дисперсия волн. Зафиксируем какое-либо значение фазы, стоящей в уравнении (28-1)

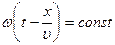. (28-3)

Продифференцируем (28-3), получим

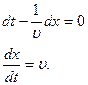
Значение 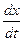дает скорость, с которой перемещается данное значение фазы.

Таким образом, скорость распространения волны 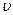в уравнении (28-1) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.

Если фазовая скорость волн в некотором частном интервале постоянна (т.е. 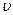не зависит от 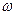), то говорят, чтодисперсия отсутствует.

Дисперсия – это зависимость фазовой скорости гармонической волны от ее частоты 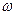. Примером волны без дисперсии является электромагнитная волна в вакууме.