Тема лекции: Кинематический анализ стержневых систем
Расчетные схемы конструкций ТиТТ подразделяются на стержневые системы и пластинчатые.
Стержневые системы, в свою очередь, можно разделить на плоские и пространственные. Такое разделение условно, так как все конструкции пространственные; однако в ряде случаев за их расчетные схемы в целях упрощения решения можно принимать плоские системы.
С кинематической точки зрения системы подразделяются на геометрически неизменяемые и геометрически изменяемые. Неизменяемой системой называется такая система, в которой изменение ее формы обуславливается лишь деформациями материала. В изменяемой системе, наоборот, элементы могут иметь относительные перемещения вне зависимости от деформаций материала системы.
Любую систему можно расчленить на элементы соединяемые и соединяющие. Соединяемые элементы называются телами, соединяющие – связями.
Определение усилий в связях представляет собой основную задачу расчета конструкций. Поэтому расчету конструкции должен предшествовать кинематический анализ выбранной расчетной схемы, т.е. установление геометрической (кинематической) структуры системы. Членение системы на тела и связи условно; оно зависит от того, что и в каком порядке подлежит дальнейшему расчету.
Каждое обособленное тело считается геометрически неизменяемым. Плоское тело называют диском, пространственное тело блоком.
Положение диска на плоскости определяется тремя координатами. Следовательно, диск имеет три степени свободы – два линейных (поступательных) перемещения и одно угловое (вращательное).
Положение блока в пространстве определяется шестью координатами. Блок, следовательно, имеет шесть степеней свободы – три линейных перемещения и три угловых.
Диски (или блоки), имеющие весьма малую площадь (объем) по сравнению с другими элементами, называются узлами. Узлы могут перемещаться лишь линейно. Степень свободы узла на плоскости равна двум, а в пространстве – трем. Каждая связь соединяет минимум два тела. Связь, соединяющая сразу несколько тел, называется кратной.
Кратность связи на единицу меньше числа соединяемых тел.
Так, например, шарнир, соединяющий одновременно четыре тела, называется трехкратным. Связи, препятствующие только взаимному поступательному перемещению тел, называются линейными, а связи, препятствующие только взаимному вращательному перемещению тел, - угловыми.
Связи обычно считаются двухсторонними, т.е. препятствующими перемещению тел в двух противоположных направлениях. Наряду с двухсторонними существуют и односторонние связи (например, трос). Однако если односторонняя связь является заведомо постоянно включенной (трос все время натянут), особенность ее работы при кинематическом анализе может не учитываться.
Основными типами связей плоских систем (рис. 1) являются: стержень С с шарнирными концами – элементарная связь, ликвидирующая одну (линейную) степень свободы соединяемых дисков; шарнир Ш – связь, эквивалентная двум элементарным и ликвидирующая две (линейные) степени свободы; заделка (припайка) П – связь, эквивалентная трем элементарным и ликвидирующая три степени свободы (две линейные и одну угловую).
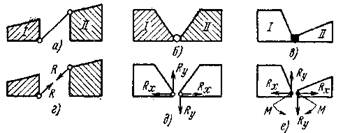
а – линейная; б – шарнирная; в – заделка (припайка); г, д и е – реакции в связях.
Рисунок 1 – Типы связей в плоских системах.
Основными типами связей пространственных систем (рис. 2) являются: стержень С с шарнирными концами – та же связь, что и в плоских системах; шарнир шаровой Шш – связь, эквивалентная трем элементарным и ликвидирующая три линейные степени свободы двух соединяемых тел; шарнир цилиндрический Шц – связь, эквивалентная пяти элементарным и допускающая поворот одного тела относительно другого только в одной плоскости; заделка (припайка) ПП – связь, эквивалентная шести элементарным и ликвидирующая все шесть степеней свободы.
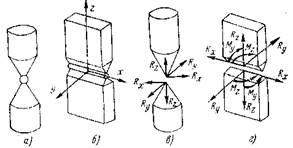
а – шаровая шарнирная; б – цилиндрическая шарнирная; в и г – реакции в связях.
Рисунок 2 – Типы связей в пространственных системах.
На рисунке 1, г – е и рисунке 2, в и г показаны усилия (реакции), которые могут возникать от внешних воздействий в связях указанных типов.
В зависимости от числа и расположения тел и связей неизменяемые системы могут быть статически определимыми или статически неопределимыми.
Степень статической неопределимости п равна числу «лишних» связей (при правильном их расположении) и определяется следующими формулами:
для плоских систем
п = (С+2Ш+3П) - (ЗД+2У-3), (5)
для пространственных систем
п = (С+3Шш+5Шц+ 6Пп) - (6Б+3У-6), (6)
В этих формулах буквами обозначены числа: Д – дисков, Б – блоков, У – узлов, С – стержней, Ш – соответствующих шарниров (с учетом их кратности) и П – соответствующих заделок (припаек).
В число дисков (или блоков) входит и «земля», если рассматриваются системы, прикрепленные к земле.
Естественно, что при п = 0 система при правильной расстановке связей будет статически определимой, а при п < 0 – заведомо изменяемой. Очевидно, что степень изменяемости системы И= - п. Судить о степени статической неопределимости (или изменяемости) системы и о правильности расстановки связей можно только после кинематического анализа, основанного на правилах образования неизменяемых систем, а также на особых признаках, вытекающих из общих методов определения усилий в связях.
На рисунках 3, а, б и 4, а, в показаны основные виды образования плоских неизменяемых систем из двух и трех дисков при минимальном количестве связей. Системы, изображенные на рисунках 3, в, г и 4, б, г, называются мгновенно изменяемыми, так как расположение связей (несмотря на их достаточное количество) позволяет дискам иметь бесконечно малые перемещения.
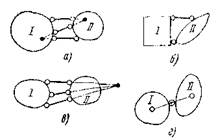
а и б – неизменяемые; в и г – мгновенно изменяемые.
Рисунок 3 – Образование плоских систем из двух дисков
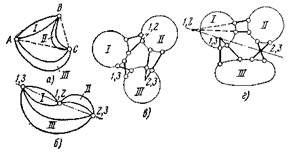
а и в – неизменяемые; б и г – мгновенно изменяемые.
Рисунок 4 – Образование плоских систем из трех дисков.
Здесь либо связи, соединяющие два диска, образуют единый мгновенный центр вращения (рис. 3, в и г), либо, что то же самое, три диска имеют три мгновенных центра вращения, лежащие а одной прямой (рис. 4, б и г).
Соединяемые и соединяющие элементы обладают свойством двойственности. Связи могут рассматриваться как тела или узлы, а тела, наоборот, как связи. Поэтому прежде чем исследовать систему, необходимо установить, что в ней принимается за соединяемые, и что за соединяющие элементы.
Основные типы образования геометрически неизменяемых пространственных систем заключается в следующем.
1. Два тела, соединяемые шестью стержнями, образуют неизменяемую систему, если при этом все шесть стержней не пересекасаются одной прямой или три стержня, лежащие в одной плоскости, не пересекаются в одной точке.
2. Присоединение узла к блоку «триадой» - тремя стержнями с шаровыми шарнирами по концам, не лежащими в одной плоскости и на одной прямой, образует неизменяемую пространственную систему.
3. Если шарнирно-стержневая система представляет собой выпуклый многогранник, в котором каждая грань неизменяема в своей плоскости, то вся система геометрически неизменяема. Такая система называется сетчатой.
Если ферма в целом (рис. 5, а) под действием сил приложенных к ее узлам, находится в равновесии, то и любой из её узлов (рис. 5, б) также находится в равновесии, т.е. внешняя нагрузка, действующая на узел, и внутренние усилия в стержнях, сходящихся в данном узле, взаимно уравновешиваются.
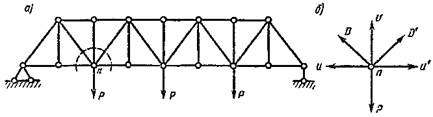
Рисунок 5 – Ферма.
На каждый узел фермы действует система сил, пересекающихся в одной точке. Для такой системы сил статика дает два уравнения равновесия:
SC = 0 и SU = 0 (7)
Если ферма имеет У узлов, то для них можно составить 2К уравнений равновесия, при помощи которых должны быть найдены усилия во всех стержнях фермы и три неизвестные опорные реакции.
Ферма будет статически определима, если число стержней её т равно удвоенному числу узлов минус 3:
т = 2У – 3 (8)
Всякая простейшая ферма, т.е. ферма, образованная из стержневого шарнирного треугольника последовательным присоединением узлов (каждого при помощи двух стержней, не лежащих на одной прямой), является системой геометрически неизменяемой и одновременно статически определимой.
Если при подсчете числа стержней m системы учесть и опорные стержни, то условие m = 2У-З примет вид:
т общ=2У (9)
Этой формулой удобно пользоваться в тех случаях, когда металлоконструкция хотя и является геометрически изменяемым (т.е. количество m его стержней меньше, чем 2У-З), но так связано с землей, что образует вместе с ней единую геометрически неизменяемую статически определимую систему.
Литература:
Основная: 3 [разд.1,с 5-7]; 4 [разд.1,с 9-19].
Контрольные вопросы.
1.На какие виды подразделяются, и на какие элементы можно расчленить любую стержневую систему?
2.Что понимается под кинематическим анализом выбранной расчетной схемы и в чем заключается принцип членения стержневой системы?
3.Сколькими координатами на плоскости и в пространстве определяются положения диска и блока?
4.Назовите основные типы связей плоских и пространственных систем?
5.Чему равна степень статической неопределимости п и какими зависимостями определяется?
6. Назовите, в чем заключаются основные типы образования геометрически неизменяемых пространственных систем и дайте определение геометрически неизменяемой и одновременно статически определимой системе?
