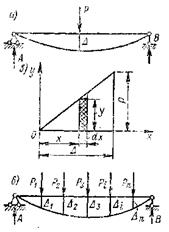
Линии влияния усилий в стержнях шпренгельных ферм

Известно, что раскосы ферм мостового типа из-за конструктивных, технологических и других соображений располагаются под углом 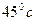поясам, поэтому в фермах с параллельными поясами панели оказываются равными высоте ферм. При больших пролетах ферм из-за больших размеров панелей в них существенно возрастают изгибающие моменты от давления ходовых колес. Чтобы уменьшит изгибающие моменты от местного давления ходовых колес, нужно уменьшит размеры панелей. С этой целью в панели основной фермы вводятся дополнительные двухопорные фермочки-шпренгели, воспринимающие местную нагрузку только в пределах данной панели.

В шпренгельных фермах следует различать три категории элементов: элементы, принадлежащие только основной ферме (усилия в них определяются так же, как и при расчете основной фермы); элементы, принадлежащие только дополнительным фермам (шпренгелям) усилия в них могут быть найдены из рассмотрения условий равновесия только шпренгельной фермочки, и элементы, принадлежащие одновременно и основной ферме и шпренгелю – усилия в них будут суммироваться из усилий в элементе основной фермы и усилия в элементе шпренгеля. На рис.29, а представлена шпренгельная ферма для езды по низу. В этой ферме стержни 1-а, 1-2, 2-3, 3-с, 3-4 и.т.д. принадлежат только к основной ферме (рис.29, б) и линии влияния у них такие же, как в основной ферме; стержни п₁ – К₁, п₁ – b, b – п₂, п₂ – К₂, п₃ – К₃, п₃ – d и т.д. принадлежат только шпренгельным фермочкам и усилия в них определяются из условия равновесия только шпренгельных элементов. На рис.29, в дан пример выделенной шпренгельной формочки, а на рис.29, г – линия влияния элементов шпренгеля, стержней 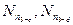. Для построения рассмотрим единичный груз в узле 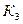. Вырезая узел d, получим:

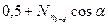, откуда 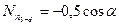. При нахождении груза в узлах c и d усилие .

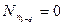В раскосе 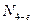на участке 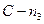усилие суммируется из усилия в основной ферме и усилия в шпренгеле (рис.29, д). Здесь правая часть линии влияния в основной ферме действительна до узла d, а переходная прямая соединяет ординаты над узлами d и с. После этого к основной линии влияния добавляется линия влияния усилия в шпренгеле на участке 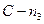, на рис.29, а заштрихованном косой штриховкой. Стержень 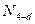(стойка) принадлежит только основной ферме, и линия влияния строится, как для обычной фермы. При единичном грузе в узле d усилие в стержне 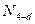равно 1, а когда груз находится в узлах с и е, усилие 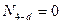(рис.29,е). 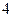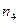Верхняя часть раскоса от узла до принадлежит только основной ферме, и её линия влияния такая же, как и для основной фермы (рис.29,ж). В нижней части раскоса 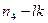основной линии влияния добавляется линии влияния в шпренгеле (рис.29, з). Аналогично строится линия влияния усилия для элемента 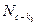(рис.29, и).

Основные теоремы об упругих системах. При проектировании металлических конструкций необходимо обеспечить не только прочность, но и жесткость системы, поэтому приходится определять расчетным путем перемещения, которые могут возникнуть в процессе эксплуатации сооружения. Перемещения необходимо определять также в процессе производства расчетов статически неопределимых систем , динамических нагрузок и т.п. Следовательно, изучение способов определения перемещений упругих систем (балок, ферм, рамных конструкций) является очень важной задачей строительной механики.

Основные понятия.

В дальнейшем будем рассматривать лишь такие системы, деформации (перемещения) которых выражаются линейными однородными функциями внешних сил. Системы, подчиняющиеся этому закону, называются линейно деформируемыми или упругими, системами. Аналитически это может быть записано так:

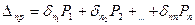, (55)

где 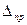– перемещение по направлению силы 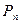от действия всех статически приложенных к сооружению сил; Р₁, Р₂, …, Р_п – силы, действующие в точках 1,2,…,п соответственно; 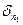-перемещение по направлению силы 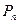от действия единичной силы 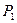, приложенной в точке 1; 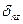– перемещение по направлению силы 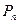от действия единичной силы 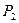, приложенной к точке 2; 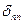– перемещение по направлению силы 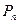от действия единичной силы 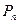, приложенной в точке n.

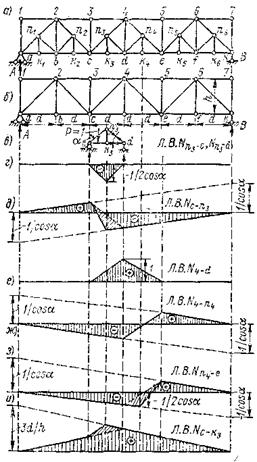
Рисунок 29 – Линии влияния усилий в стержнях шпренгельной фермы.

Выражение (55), представляющее собой линейную зависимость перемещений от действующих сил, иногда называют обобщенным законом Гука. В частном случае, когда имеется лишь одна сила 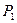, а остальные силы равны нулю, получаем выражение 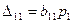. Перемещения и деформации рассматриваемых систем подчиняются закону независимости действия сил при следующих допущениях: материал конструкции является идеально упругим и линейно деформируемым, т.е. напряжения материала от действующей не превышают его предела пропорциональности; поверхности взаимно перемещающихся элементов являются идеально гладкими (трение отсутствует); по своей структуре конструкции геометрически неизменяемы; изменения в конструкциях от воздействия нагрузки ничтожно малы по сравнению с их размерами.

Наличие трения в шарнирах, заклепочных и болтовых соединениях, а также наличие напряжений в отдельных волокнах элементов выше предела пропорциональности вносят некоторые незначительные поправки к линейному закону общих деформаций системы, но ими обычно пренебрегают.

Для более глубокого изучения свойств упругого тела анализируют работу внешних и внутренних сил, действующих на тело. При этом в строительной механике пользуются понятиями об обобщенной силе, обобщенном перемещении и обобщенной работе. Под обобщенной работой понимается произведение двух факторов, из которых один зависит от силы (момента), а другой от перемещения (угла поворота). Например: если к телу приложена пара сил c моментом М=P·h, то при повороте тела на угол 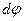работа пары будет равна (рис.30, а) 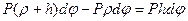. В этом случае момент пары M=P· h будет обобщенной силой, а угол поворота 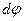– обобщенным перемещением.

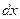Пусть на балку действует равномерно распределенная нагрузка интенсивностью (рис.30,б), под действием которой балка прогнется и совершит работу. Выделим элемент .Элементарная работа линейно возрастающей от нуля сосредоточенной силы 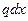будет 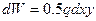,а полное ее значение 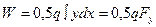. В этом случае распределенная нагрузка q является обобщенной силой, а 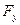– площадь, заключенная между первоначальной осью балки и упругой линией, – обобщенным перемещением. Эти примеры показывают, что обобщенные силы и перемещения могут иметь различную размерность работы.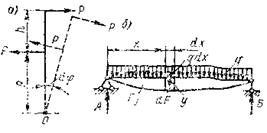

Рисунок 30 – Определение обобщенной работы

Рисунок 31 – Определение работы при

статическом действии сил.