Графический метод определения усилий
При графическом методе определения усилий в стержнях фермы при действии неподвижной нагрузки производят вырезание узлов и построение замкнутых многоугольников действующих сил. Перед построением должны быть определены опорные реакции. Построение начинается с такого узла, где сходятся не более двух стержней, т.е. с опорного узла (рис. 22, а).
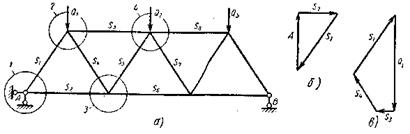
Рисунок 22 – Определение усилий в стержнях методом построения силовых многоугольников.
Рассмотрим узел 1, в котором действуют опорная реакция А и усилия стержней S1 и S2. разложим реакцию А по направлениям осей стержней и построим замкнутый треугольник сил (рис. 22, б), в котором стороны треугольника будут показывать направление действия сил, а по величине будут пропорциональны величинам сил. Затем рассматриваем узел 2 (рис. 22, в) и далее узлы 3, 4 и остальные узлы фермы. При построении необходимо иметь ввиду, что: число стороны диаграммы равно числу стержней фермы; линии на диаграмме соответственно параллельны осям стержней фермы; каждому узлу фермы соответствует замкнутый многоугольник.
Шпренгельные фермы.
Усилия в стержнях ферм способом моментной точки определяется по формуле
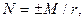
где М- момент левых или правых сил относительно моментной точки; r – плечо усилия N относительно этой точки.
Из этой формулы видно, что чем больше r, тем меньше (при прочих равных условиях) усилие N. Увеличение высоты фермы приводит к увеличению плеч r и уменьшению усилий в ее элементах.
По конструктивным соображениям удобно располагать раскосы фермы так, чтобы они составляли со стойками и поясами углы, близкие к 450. поэтому увеличение высоты ферм приводит к увеличению длины панелей. Так, например для соблюдения этого условия панели фермы с параллельными поясами должны быть примерно равны высоте фермы (рис. 23, а).
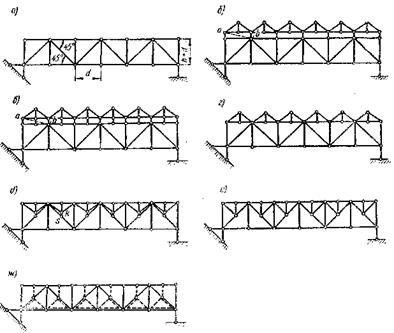
Рисунок 23-Шпренгельные фермы.
Задача увеличения высоты фермы может быть рационально решена при введении в состав каждой панели дополнительных двухопорных фермочек – шпренгелей (рис. 23,б), опирающихся на узлы основной фермы. Стержни таких фермочек работают лишь на местную нагрузку, т.е. на нагрузку, приложенную в пределах их пролетов. Вертикальная местная нагрузка, действующая на шпренгель, передается вертикально же в узлы основной фермы, которые являются для шпренгелья опорами. Стержень, аb (штриховая линия на рис. 23, б) необходим только для обеспечения геометрической неизменяемости системы; усилие в нем равно нулю. Шпренгели позволяют поставить поперечные балки не только в основных узлах фермы, но и в дополнительных и уменьшить за счет этого сечения вспомогательных балок; в результате существенно облегчается проезжая часть моста. Применение шпренгелей позволяет избежать увеличения массы проезжей части моста при возрастании длины панели и добиться уменьшения усилия в поясах фермы путем увеличения ее высоты. Связав подвесками нижние дополнительные узлы шпренгелей шарнирами, поставленными посередине каждого из элементов верхнего пояса основной системы, получим ферму, изображенную на рис. 23, в, которая работает совершенно так же, как и ферма без подвесок (рис. 23, б). Уменьшив затем длины подвесок и вертикальных опорных стержней (при помощи которых шпренгели опираются на узлы основной фермы) и сделав их в пределе равными нулю получим ферму, изображенную на рис. 23, г. В этой ферме нижние пояса шпренгелей сливаются с элементами верхнего пояса основной фермы. По характеру работы такая ферма аналогична ферме со шпренгелями, изображенной на рис. 23, д. Усилия в подвесках RS последней фермы равны нулю. Практически длину каждой такой подвески делают равной нулю, т.е. совмещают узел R с узлом S. В результате получается ферма изображенная на рис. 23, е. которая носит название шпренгельной, или фермы со шпренгелями.
Шпренгели, изображенные на рис. 23,е, передают местную вертикальную нагрузку, приложенную к верхним дополнительным узлам, вертикально в верхние узлы основной фермы. Такие шпренгели условимся называть одноярусными. Применяются также шпренгели, которые местную нагрузку, приложенную к верхним узлам, передают на нижние узлы основной фермы (рис. 23, ж), или такие, которые нагрузку, приложенную к дополнительным узлам нижнего пояса, передают на верхние узлы основной фермы. Такие шпренгели будем называть двухъярусными.
Элементы ферм, в состав которых входят одноярусные шпренгели, можно разбить на следующие три категории:
- элементы, принадлежащие только основной, ферме. Усилия в этих элементах определяются расчетом основной фермы; эти усилия не меняются при включении в ферму шпренгелей;
- элементы, принадлежащие только дополнительным фермам (шпренгелем). Усилия в них могут быть найдены из условий равновесия, составляемых для отдельных частей шпренгеля, который при этом можно рассматривать как самостоятельную двухопорную ферму;
- элементы, принадлежащие одновременно основной ферме и шпренгелю. Усилие в каждом из них равно сумме двух усилий, одно из которых возникает в элементе основной фермы, а другое – в слившемся с ним элементе шпренгеля.
Элементы ферм, в состав которых входят двухярусные шпренгели, делятся на четыре категории: из них первые три же, что и для ферм с одноярусными шпренгелями, элементами четвертой категории являются те из элементов основной фермы (первой категории), линии влияния для которых имеют различный вид при езде поверху и при езде понизу.
Линии влияния.
Этот метод удобен для определения в связях в том случае, если нагрузки перемещаются по конструкции, не изменяя своего направления. Метод линий влияния удобно использовать и для определения усилий от системы сосредоточенных и распределенных нагрузок, действующих в одном направлении.
Линий влияния, какого – либо усилия называется графическое изображение закона изменения данного усилия в этом сечении при перемещении силы 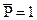 по длине конструкции. Применяя принцип независимости, изучают сначала действие лишь одной силы Р=1, а затем, зная усилия от единичной силы, находят полное усилие от
по длине конструкции. Применяя принцип независимости, изучают сначала действие лишь одной силы Р=1, а затем, зная усилия от единичной силы, находят полное усилие от 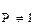 или от системы сил. Для построения любой линии влияния усилия применяют статический или кинематический метод.
или от системы сил. Для построения любой линии влияния усилия применяют статический или кинематический метод.
При статическом методе нагрузку 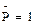 помещают в произвольную точку, определяемую абсциссой Х, и исходя из условия равновесия выводят уравнение искомого усилия; затем выражают это графически. Иногда единичную нагрузку приходится помещать поочередно в нескольких участках и для каждого из них выводить свое уравнение. Линия влияния в этом случае будет состоять из участков, имеющих различные уравнения. Определим линии влияния опорных реакций, изгибающего момента в сечениях С и Д и поперечных сил в тех же сечениях для статически определимой балки, изображенной на рис. 24,а.
помещают в произвольную точку, определяемую абсциссой Х, и исходя из условия равновесия выводят уравнение искомого усилия; затем выражают это графически. Иногда единичную нагрузку приходится помещать поочередно в нескольких участках и для каждого из них выводить свое уравнение. Линия влияния в этом случае будет состоять из участков, имеющих различные уравнения. Определим линии влияния опорных реакций, изгибающего момента в сечениях С и Д и поперечных сил в тех же сечениях для статически определимой балки, изображенной на рис. 24,а.
Запишем уравнения моментов относительно опоры В:
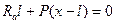 (40)
(40) 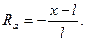 (41)
(41)
Это уравнение является уравнением прямой, для которой при Х = 0 RА=1, при Х=l RА=0. линия влияния для RА показана на рис. 24,б.
Реакция в опоре А равна единице, когда нагрузка Р=1 стоит над опорой, и уменьшается по линейному закону до нуля, когда нагрузка приближается к опоре В.
Из уравнения моментов относительно опоры А аналогичным образом получим уравнения реакции для опоры В (рис. 24,в):
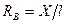 (42)
(42)
Для построения линии влияния изгибающего момента в сечении С запишем следующие уравнения: при расположении силы 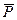 =1 слева от сечения С (
=1 слева от сечения С ( 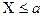 )
) 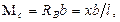 т.е. влияния изгибающего момента в сечении С представляет собой линию влияния опорной реакции Rв, умноженную на постоянное число b; при расположении силы
т.е. влияния изгибающего момента в сечении С представляет собой линию влияния опорной реакции Rв, умноженную на постоянное число b; при расположении силы 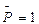 справа от сечения С (х
справа от сечения С (х 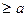 )
) 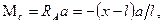 т.е. линия влияния Мс представляет собой линию влияния опорной реакции RА, умноженную на постоянное число а.
т.е. линия влияния Мс представляет собой линию влияния опорной реакции RА, умноженную на постоянное число а.
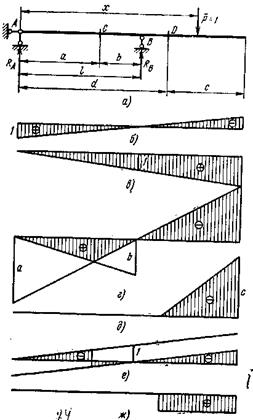
а – расчетная схема; б и в – линии влияния опорных реакций соответственно RA и RВ; г и д – линии влияния изгибающих моментов соответственно Мс и Мд; е и ж – линии влияния поперечных сил соответственно Qc и Qд
Рисунок 24 – Линии влияния в балке.
Линия влияния Мс показана на рис. 24,г, где за положительный момент принят тот, который вызывает растяжение в нижнем волокне сечения.
Вид линии влияния изгибающего момента в сечении Д определится из следующих рассуждений. Если силу 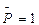 расположить слева от сечения Д, то МД=0. Если силу
расположить слева от сечения Д, то МД=0. Если силу 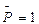 расположить справа от сечения Д, то изгибающий момент определится формулой
расположить справа от сечения Д, то изгибающий момент определится формулой 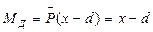 . В случае расположения груза на конце консоли МД=С. Следовательно, линия влияния МД будет иметь вид, изображенный на рис. 24, д. Если нагрузка
. В случае расположения груза на конце консоли МД=С. Следовательно, линия влияния МД будет иметь вид, изображенный на рис. 24, д. Если нагрузка 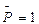 расположена справа от сечения С, то поперечная сила Qс будет равна RА. Если нагрузку
расположена справа от сечения С, то поперечная сила Qс будет равна RА. Если нагрузку 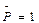 расположить слева от сечения С, то поперечная сила в сечении С будет направлена вниз и равна по величине
расположить слева от сечения С, то поперечная сила в сечении С будет направлена вниз и равна по величине 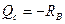 . Таким образом, в первом случае линия влияния Qс будет равна линии влияния RА, а во втором – линии влияния RВ с обратным знаком. На рис. 24, е видно, что обе ветви линии влияния поперечной силы Qс параллельны друг другу и под сечением С имеют скачок (разрыв), равный 1.
. Таким образом, в первом случае линия влияния Qс будет равна линии влияния RА, а во втором – линии влияния RВ с обратным знаком. На рис. 24, е видно, что обе ветви линии влияния поперечной силы Qс параллельны друг другу и под сечением С имеют скачок (разрыв), равный 1.
Линия влияния поперечной силы QД также состоит из двух параллельных прямых (рис. 24, ж) с ординатой, равной 1. Анализ формул линий влияния позволяет установить, что ординаты линий влияния опорных реакций и поперечных сил выражаются отвлеченными числами, а размерность линий влияния изгибающих моментов – мерой длины (см, м и т.д.)
Кинематический метод построения линий влияния основан на принципе возможных перемещений. По этому методу каждую линию влияния усилия находят по эпюре перемещений основной системы, полученной после отбрасывания той связи. В которой возникает рассматриваемое усилие. Так как система должна находиться в равновесии, то согласно принципу возможных перемещений записывается уравнение
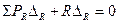 , (43)
, (43)
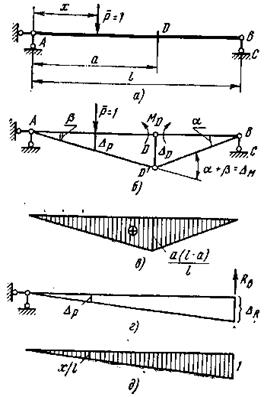
исходя из которого и определяется искомое усилие R. Построим линию влияния изгибающего момента в сечении Д в однопролетной балке (рис. 25,а) кинематическим методом. Отбросим в сечении Д ту связь, которая передает изгибающий момент МД, т.е. снимем жесткое соединение соседних сечений. Оставляя в сечении Д лишь шарнирное соединение, жесткое соединение возместим парным моментом МД. Возможное перемещение полученного шарнирного механизма АДВС определяется поворотом звена АД на угол β и звена ВД на угол 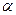 (рис. 25,б). Согласно формуле (43)
(рис. 25,б). Согласно формуле (43)
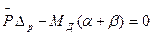 (44)
(44)
Момент Мд взят со знаком «минус» так как действующий момент противоположен направлению перемещения 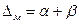 .
.
Из этого уравнения получим
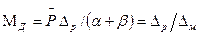 (45)
(45)
Следовательно, линия влияния МД представляет собой эпюру вертикальных перемещений 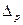 , подставляя в выражение (45)* значения
, подставляя в выражение (45)* значения 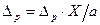 и
и 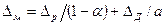 , получим уравнение левой части линии влияния МД
, получим уравнение левой части линии влияния МД
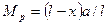 (46)
(46)
Аналогичным образом находим уравнение правой ветви линии влияния МД. Линия влияния МД представлено на рис. 25, в.
Для построения линии влияния опорной реакции Rв кинематическим методом (рис. 25, г,д) согласно уравнению (43)
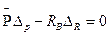 откуда
откуда 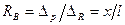 .
.
При построении линии влияния усилий в стержнях ферм можно использовать статический или кинематический метод определения в связях.
Для построения линии в линии усилия, в каком – либо стержне фермы статическим методом необходимо нагрузки 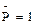 установить в произвольном узле фермы и составить уравнения искомого усилия; затем это уравнения исследовать, чтобы определить характер линии влияния.
установить в произвольном узле фермы и составить уравнения искомого усилия; затем это уравнения исследовать, чтобы определить характер линии влияния.
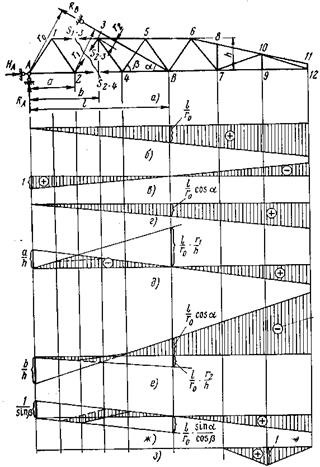
Построим линии влияния для стержней 1-3 (рис.26),2-3, 3-4 и 9-10 стрелы башенного крана при движении нагрузки 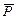 =1 по нижнему и по верхнему поясам. Предварительно построим линии влияния опорных реакций. Уравнение линии влияния усилия
=1 по нижнему и по верхнему поясам. Предварительно построим линии влияния опорных реакций. Уравнение линии влияния усилия 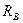 в подвеске стрелы (в опоре В) определится из условия равенства нулю сумму моментов относительно опоры А.
в подвеске стрелы (в опоре В) определится из условия равенства нулю сумму моментов относительно опоры А.
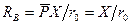 (47)
(47)
Линия влияния 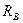 в опоре изображена на рис.26, б. Аналогичным образом, рассматривая изменение момента относительно опоры В построим линию влияния опорной реакции
в опоре изображена на рис.26, б. Аналогичным образом, рассматривая изменение момента относительно опоры В построим линию влияния опорной реакции  (рис.26.в).
(рис.26.в).
|
| |||
| |||
Линия влияния горизонтальной составляющей реакции 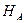 , (рис.24, г) определится из уравнения для реакции
, (рис.24, г) определится из уравнения для реакции 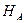 , которая находится из суммы проекций всех сил на горизонталь:
, которая находится из суммы проекций всех сил на горизонталь:
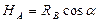 (48)
(48)
Для построения линии влияния усилий в стержнях 1-3, 2-3 и 2-4 проведем сечения через эти стержни и воспользуемся моментной точкой 2 для определения 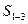 .При расположении нагрузки
.При расположении нагрузки  справка от сечения
справка от сечения 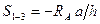 .
.
Линия влияния 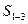 представляет собой линию влияния опорной реакции
представляет собой линию влияния опорной реакции 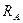 взятой с обратной знаком и умноженной на коэффициент
взятой с обратной знаком и умноженной на коэффициент 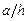 . В этом случае линия влияния
. В этом случае линия влияния 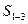 справедлива при движении силы по нижнему поясу на участке 4-12 и по верхнему поясу на участке 3-11.
справедлива при движении силы по нижнему поясу на участке 4-12 и по верхнему поясу на участке 3-11.
Располагая нагрузку 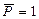 слева от сечения, получим
слева от сечения, получим
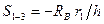 , (49)
, (49)
т.е. линия влияния 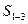 представляет
представляет  собой линию влияния опорной реакции
собой линию влияния опорной реакции 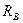 , взятой с обратным знаком и умноженной на коэффициент
, взятой с обратным знаком и умноженной на коэффициент 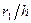 .
.
В этом случае линия влияния 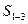 справедлива при движении силы по нижнему поясу на участке А-2 и по верхнему поясу на участке А-1. Участок линии влияния между точками 2-4 и 1-3 следует соединить прямыми. На рис.26, д сплошной линией изображена линия
справедлива при движении силы по нижнему поясу на участке А-2 и по верхнему поясу на участке А-1. Участок линии влияния между точками 2-4 и 1-3 следует соединить прямыми. На рис.26, д сплошной линией изображена линия 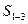 при движении силы
при движении силы 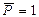 по нижнему поясу и пунктирной – по верхнему поясу.
по нижнему поясу и пунктирной – по верхнему поясу.
Уравнение линии влияния усилия в стержне 2-4 определим из условия равновесия левой части отсеченной фермы (при силе  , расположенной справа от сечения) относительно моментной точки 3:
, расположенной справа от сечения) относительно моментной точки 3:
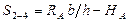 . (50)
. (50)
Ордината линии влияния при нагрузке, расположенной на опоре А, будет 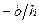 , а при нагрузке, расположенной на опоре В, составит
, а при нагрузке, расположенной на опоре В, составит 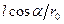 .
.
Из условия равновесия правой отсеченной части фермы (при силе  , Расположенной от сечения) относительно той же моментной точки уравнение линии влияния будет
, Расположенной от сечения) относительно той же моментной точки уравнение линии влияния будет
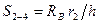 . (51)
. (51)
Линия влияния 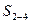 в стержне построена на рис. 18,е.Линию влияния усилия в стержне 2-3 найдем из суммы проекций всех сил на вертикаль. Рассматривая в равновесии левую отсеченную часть фермы (груз р=1 справа от сечения), получим
в стержне построена на рис. 18,е.Линию влияния усилия в стержне 2-3 найдем из суммы проекций всех сил на вертикаль. Рассматривая в равновесии левую отсеченную часть фермы (груз р=1 справа от сечения), получим
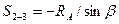 . (52)
. (52)
Рассматривая правую отсеченную часть фермы (груз  слева от сечения), получим
слева от сечения), получим
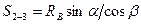 (53)
(53)
Линия влияния усилия 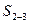 построена на рис.26, ж. Линию влияния усилия в подвеске 9-10 (рис.26, з) определим, вырезав узел 9.
построена на рис.26, ж. Линию влияния усилия в подвеске 9-10 (рис.26, з) определим, вырезав узел 9.
При расположении груза  непосредственно в узле 9
непосредственно в узле 9 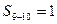 , а при расположении в других узлах
, а при расположении в других узлах 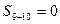 . Следовательно, при движении груза
. Следовательно, при движении груза  по нижнему поясу линия влияния усилия в подвеске 9-10 представляет собой треугольник. При движении груза по верхнему поясу подвеска не испытывает нагрузок.
по нижнему поясу линия влияния усилия в подвеске 9-10 представляет собой треугольник. При движении груза по верхнему поясу подвеска не испытывает нагрузок.
Рассмотрим способы определения усилия от некоторых нагрузок по линиям влияния.
Если на конструкцию действует неподвижная система сосредоточенных сил и построена линия влияния искомого усилия (рис.27), то величина его согласно принципу независимости действия сил будет
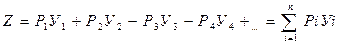 (54)
(54)
На участках линии влияния с одинаковым углом наклона систему сил можно заменить равнодействующей. Тогда величина искомого усилия будет
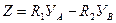
Усилие от неподвижной сплошной нагрузки определяют следующим образом.
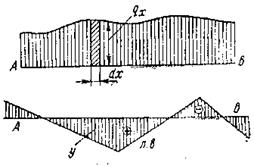
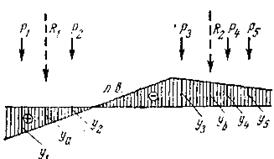
Выделяется элементарный участок dx (рис.28)с интенсивностью нагрузки 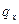 , которую можно рассматривать как сосредоточенную нагрузку. Влияние этой нагрузки будет равно
, которую можно рассматривать как сосредоточенную нагрузку. Влияние этой нагрузки будет равно 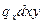 , где у – ордината линии влияния искомого усилия под центром тяжести нагрузки
, где у – ордината линии влияния искомого усилия под центром тяжести нагрузки 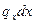 .
.
Следовательно, искомое усилие при действии сплошной равномерно распределенной нагрузки равно произведению площади загруженного участка линии влияния на интенсивность нагрузки 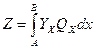
|
|
|
Литература: Основная: 5[разр.2,с.246-250]; 4[разр.4,с.164-166]; 3 [разр.1,с.21-28].
Контрольные вопросы.
1 При расчете металлоконструкций ТиТТ методами строительной механики, какой принцип следует использовать и какими методами можно определять усилия в стержнях?
2 Как производится определение усилий в элементах ферм при неподвижной нагрузке и какие типы ферм находят наибольшее распространение в ТиТТ?
3 Назовите аналитические методы определения усилий в стержневых системах ТиТТ, а также объясните их сущность?
4 В чем заключается сущность графического метода определения усилий в стержнях фермы и по какой зависимости и каким способом определяются усилия в стержнях ферм?
5 На сколько и какие категории можно разбить элементы ферм, в состав которых входят одноярусные шпренгели, а также на сколько категорий делятся элементы ферм, в состав которых входят двухъярусные шпренгели?
6 Что называется линией влияния какого-либо усилия и какой метод применяют для построения её, а также покажите определение и построение линии влияния опорных реакций, изгибающего момента в указанных сечениях и поперечных сил для статические определимой баллы?