Энергия ветра. Коэффициент использования энергии ветра. Работа ветрового колеса крыльчатого ветродвигателя
Поток ветра с поперечным сечением F обладает кинетической энергией, определяемой выражением:
Масса воздуха, протекающая через поперечное сечение F со ско-ростью V, равна:
m = rFV. (2)
Тогда кинетическая энергия ветра:
| 2 2 |
Из (3) следует, что энергия ветра изменяется пропорционально кубу его скорости.
Посмотрим, сколько процентов энергии ветра может превратить в полезную работу поверхность, поставленная перпендикулярно к направлению ветра и перемещающаяся в этом же направлении, что имеет место, например, у ветродвигателей карусельного типа.
Мощность T определяется произведением силы P на скорость V:
T = PV. (4)
Допустим, мы имеем поверхность F, поставленную перпендику-лярно к направлению ветра (рисунок 1)
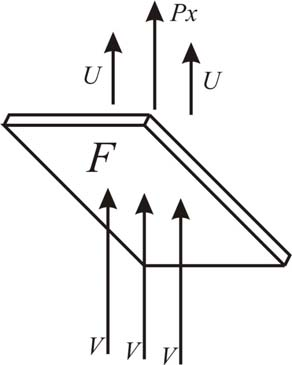Рисунок. 1 -. Действие силы ветра на поверхность
Воздушный поток вследствие торможения его поверхностью получит подпор и будет обтекать её и производить давление силой Px. Вследствие действия этой силы поверхность будет перемещаться в направлении потока с некоторой скоростью U (рис. 7.10); работа Т при этом будет равна произведению силы на скорость U, с которой перемещается поверхность F, то есть:
| x |
где Px– сила сопротивления, которая равна:
| x |
где Cx– аэродинамический коэффициент лобового сопротивления; F – поверхность миделевого сечения тела, т. е. проекции площади тела на плоскость, перпендикулярную направлению воздушного потока.
В этом случае ветер набегает на поверхность с относительной скоростью, равной:
W =V - U. (7)
Подставив значение Pxиз уравнения (7.3.6) в уравнение (7.3.5), получим:
(8)
Определим отношение работы, развиваемой движущейся поверхностью и выраженной уравнением (7.3.8), к энергии ветрового потока, имеющего поперечное сечение, равное этой поверхности, а именно:
(9)
Величину называют коэффициентом использования энергии ветра, зависит от скорости перемещения поверхности в направлении ветра. При некотором значении скорости U коэффициент получает максимальное значение. В самом деле, если скорость перемещения поверхности равна нулю U = 0, то работа ветра также равна нулю. Если U = V, т. е. поверхность перемещается со скоростью ветра, работа также будет равна нулю. Отсюда следует, что значение скорости U заключено в пределах между U = 0 и U = V. Установлено, чтобы получить максимальное поверхность должна перемещаться со скоростью:
U=V/3 (10)
Максимальный коэффициент использования энергии ветра при работе поверхности силой сопротивления не может быть больше = 0,192.
Работаветровогоколесакрыльчатоговетродвигателя
Крыльчатые ветроколеса работают за счёт косого удара при движении лопастей перпендикулярно к направлению скорости ветра в противоположность к прямому удару, рассмотренному в предыдущем случае. Устройство такого колеса показано на рисунке 2.
На горизонтальном валу закреплены крылья, число которых у современных ветродвигателей бывает от двух и больше. Крыло ветроколеса состоит из маха а и лопасти б, закрепляемой на махе так, что она образует с плоскостью вращения некоторый угол j . Этот угол называют углом заклинения лопасти (рисунок 2).
При этом на её элементы набегает воздушный поток с относитель-ной скоростью W под углом α , который называют углом атаки, и дей-ствует с силой R. Углы j и α в значительной мере определяют эффективность крыльев.
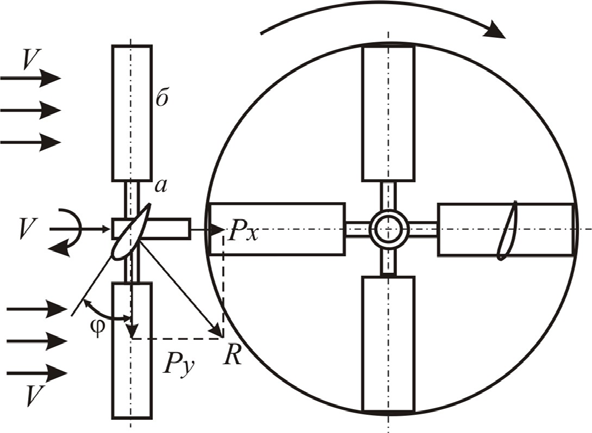
Рисунок.2 - Конструктивная схема крыльчатого ветроколеса
Силу R раскладывают на силы Pxи Py(рисунок 3). Силы Pxпроизводят давление в направлении ветра, которое называется лобовым давлением. Силы Pyдействуют в плоскости y – y вращения ветроколеса и создают крутящий момент.
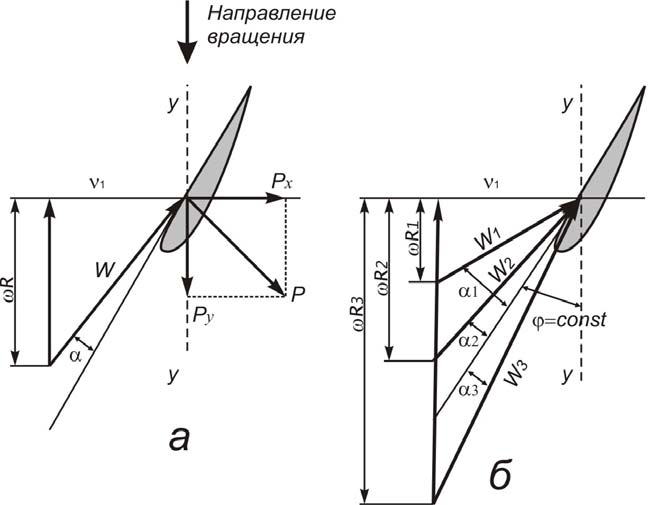
Рисунок 3 - а – схема действия сил воздушного потока на элемент лопасти; б – графическое изображение относительного потока, набегающего на элементы лопасти, расположенные на разных радиусах ветроколеса
Максимальные силы, приводящие колесо во вращение, получаются при некотором значении угла атаки α , т. е. угла наклона относительного потока к поверхности лопасти. Ввиду того что окружная скорость по длине крыла не одинакова, а возрастает по мере удаления его элементов от оси вращения ветроколеса, относительная скорость W набегания потока на лопасть также возрастает. Вместе с этим убывает угол атаки α , и при некоторой окружной скорости ωR, где ω угловая скорость, этот угол станет отрицательным (рисунок 3,б). Следовательно, не все элементы крыла будут иметь максимальную подъёмную силу.
Если мы будем уменьшать угол jкаждого элемента лопасти по мере удаления его от оси вращения так, чтобы наивыгоднейший угол атаки α примерно сохранялся постоянным, то мы получим условие, при котором приблизительно все элементы лопасти будут работать со своей максимальной подъёмной силой. Лопасть с переменным углом заклинения получает форму винтовой поверхности.
Правильные углы заклинения лопасти при хорошем аэродинамическом качестве профиля, а также ширине, соответствующей заданной быстроходности, обеспечивают высокий коэффициент использования энергии ветра.У хорошо выполненных моделей он достигает 46 %.
Идеальным ветряком называют ветроколесо, у которого:
1. Ось вращения параллельна скорости ветра.
2. Бесконечно большое число лопастей очень малой ширины.
3. Профильное сопротивление крыльев равно нулю, и циркуляция вдоль лопасти постоянна.
4. Потерянная скорость воздушного потока на ветроколесе постоянна по всей сметаемой поверхности ветряка.
5. Угловая скорость стремится к бесконечности
Представим равномерный поток ветра, набегающий на идеальное ветроколесо со скоростью V в сечении AA′' (рисунок 4). В сечении BB′ на ветроколесе скорость будет V1 =V – v1 на некотором расстоянии позади ветряка в сечении CC′ скорость будет V2=V –v2., где v1, v2 – потери скорости
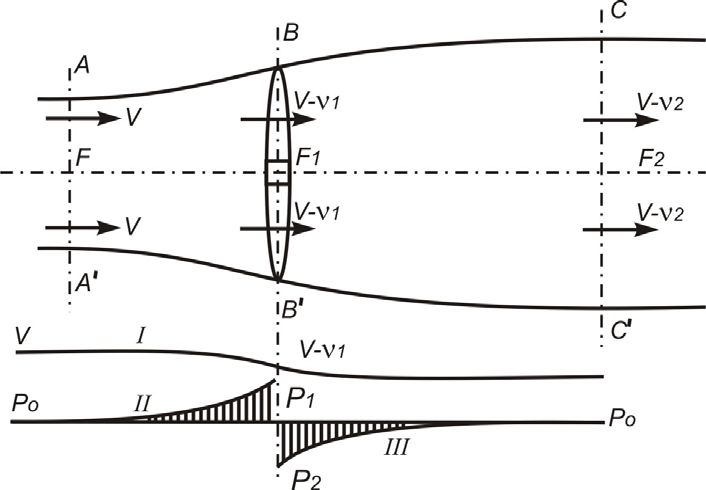
Рисунок 4 - Характеристика воздушного потока, протекающего через ветроколесо
Выражение
(11)
называют коэффициентом нагрузки на ометаемую площадь или коэффициентом лобового давления. Здесь е=V1/V - коэффициент торможения.
Коэффиент использования энергии ветра
(12)
Он принимает максимальное значение , когда е=1/3. При этом В=0,888
Таким образом, из классической теории идеального ветряка выте-кают следующие основные положения:
1. Максимальный коэффициент использования энергии ветра иде-ального ветроколеса равен
x= 0,593.
2. Потеря скорости ветра в плоскости ветроколеса
V1=1/3V
3. Полная потеря скорости ветра за ветроколесом в два раза больше потери скорости в плоскости ветроколеса
V2=2/3V
Таким образом, скорость ветра за ветроколесом в три раза меньше скорости ветра перед ветроколесом.
4. Коэффициент нагрузки на ометаемую поверхность ветроколеса равен
B =0,888.
Мощность пропеллерного ветроколеса определяется выражением
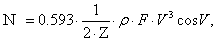Вт. (13)
Здесь: 0,593 – аэродинамический коэффициент использования энергии ветра,
Z – коэффициент порывистости и частоты изменения направления;
p – плотность ветра,
F – площадь активной поверхности ветроколеса;
V – скорость ветра;
CosV – соответствие положения ветроколеса и установки лопастей направлению и скорости ветра.
Комплекс параметров Z, p, V характеризует свойства ветра, F – размеры и аэродинамическое совершенство ветроколеса, CosV – характеризует качество управления ветроколесом по установке на ветер.