Расчет переходного процесса методом трапеций

Вещественную частотную характеристику (рисунок 7) заменим мало отличающимися от кривой горизонтальными и наклонными прямолинейными участками, образующими с осью ординат трапеции. Действительная ВЧХ при этом будет представлена как алгебраическая сумма трапецеидальных частотных характеристик

,

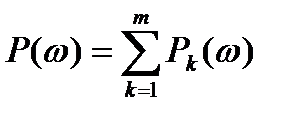где 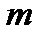‑ число трапеций.

Горизонтальные отрезки чертим в точках экстремумов. Первый отрезок должен начинаться из точки 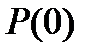, т.к. эта точка определяет конечное значение переходной характеристики 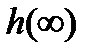. Более тщательно нужно аппроксимировать начальный участок ВЧХ. Конечный участок с ординатами, меньшими по абсолютному значению, чем 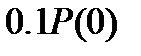можно не принимать во внимание.

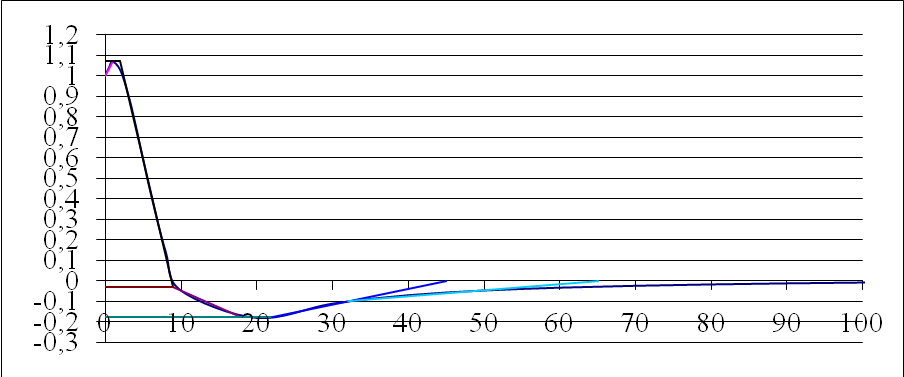
Рисунок 8 – Замена вещественной частотной характеристики трапециями

Полученные трапеции вычертим на другом чертеже (рисунок 9) таким образом, чтобы основание каждой из них легло на ось .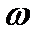

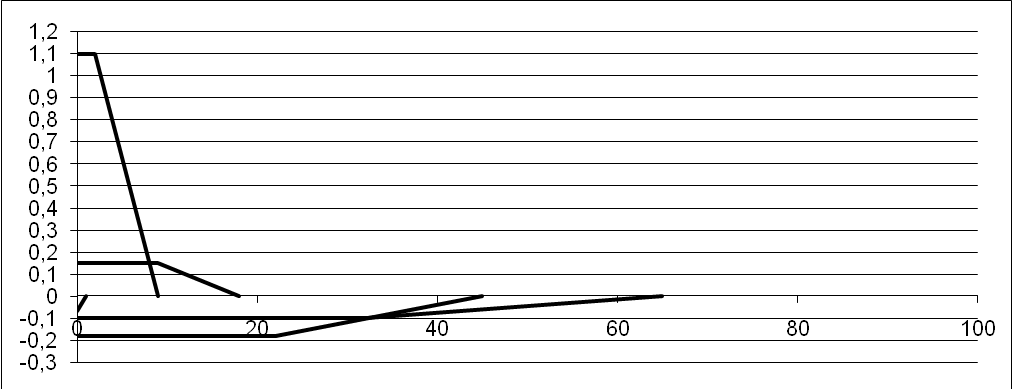
Рисунок 9 – Трапеции вещественной частотной характеристики

Определим параметры трапеций.

Из графиков находим

,

.

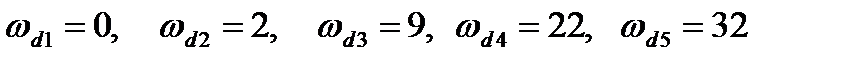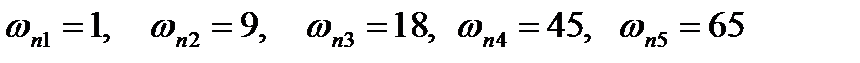
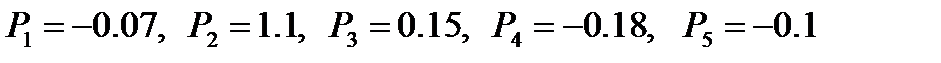По значениям 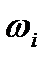вычислим коэффициенты наклона

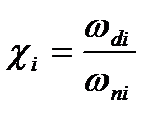
и округлим их до ближайшего из значений 0; 0,05; 0,1; 0,15; … 0,95; 1.

Подставив численные значения, получим

.

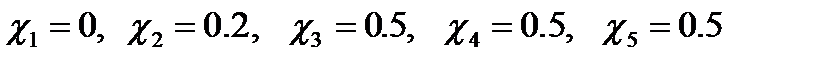Рассчитаем переходные процессы отдельно для каждой трапеции.

В таблице h-функций таблица 4.2 с.222 [3] для каждой i-й трапеции отыскивается столбец, соответствующий значению коэффициента наклона .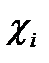

Затем для ряда значений условного времени 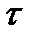выписывают соответствующие им значения 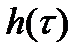. По значениям 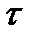и 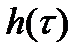вычисляют значения действительного времени 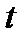и составляющей переходной характеристики :

;

.

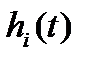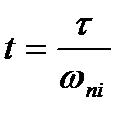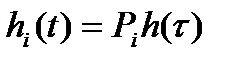Результаты оформим в таблице 5.

Таблица 5 – Расчет графиков составляющих переходной характеристики

Трапеция 1	Трапеция 2	Трапеция 3
wn=1 Р=-0.07 c=0	wn=9 Р=1,1 c=0,2	wn=18 Р=0,15 c=0,5
t	h(t)	t	h(t)	t	h(t)	t	h(t)	t	h(t)	t	h(t)
0,5	0.124	0,5		0,5	0,192	0,05555556	0,2112	0,5	0,24	0,0277778	0,036
	0,138		-0,00966		0,371	0,11111111	0,4081		0,461	0,0555556	0,06915
1,5	0,31	1,5	-0,0217	1,5	0,538	0,16666667	0,5918	1,5	0,665	0,0833333	0,09975
	0,449		-0,03143		0,683	0,22222222	0,7513		0,833	0,1111111	0,12495
2,5	0,572	2,5	-0,04004	2,5	0,867	0,27777778	0,9537	2,5	0,967	0,1388889	0,14505
	0,674		-0,04718		0,896	0,33333333	0,9856		1,061	0,1666667	0,15915
3,5	0,755	3,5	-0,05285	3,5	0,963	0,38888889	1,0593	3,5	1,115	0,1944444	0,16725
	0,783		-0,05481		1,008	0,44444444	1,1088		1,142	0,2222222	0,1713
4,5	0,857	4,5	-0,05999	4,5	1,029	0,5	1,1319	4,5	1,138	0,25	0,1707
	0,883		-0,06181		1,042	0,55555556	1,1462		1,118	0,2777778	0,1677
5,5	0,896	5,5	-0,06272	5,5	1,046	0,61111111	1,1506	5,5	1,092	0,3055556	0,1638
	0,9		-0,063		1,037	0,66666667	1,1407		1,051	0,3333333	0,15765
6,5	0,904	6,5	-0,06328	6,5	1,03	0,72222222	1,133	6,5	1,018	0,3611111	0,1527
	0,904		-0,06328		1,024	0,77777778	1,1264		0,993	0,3888889	0,14895
7,5	0,904	7,5	-0,06328	7,5	1,019	0,83333333	1,1209	7,5	0,974	0,4166667	0,1461
	0,907		-0,06349		1,02	0,88888889	1,122		0,966	0,4444444	0,1449
8,5	0,91	8,5	-0,0637	8,5	1,021	0,94444444	1,1231	8,5	0,966	0,4722222	0,1449
	0,918		-0,06426		1,02		1,122		0,97	0,5	0,1455
9,5	0,924	9,5	-0,06468	9,5	1,029	1,05555556	1,1319	9,5	0,975	0,5277778	0,14625
	0,932		-0,06524		1,031	1,11111111	1,1341		0,982	0,5555556	0,1473
10,5	0,939	10,5	-0,06573	10,5	1,033	1,16666667	1,1363	10,5	0,987	0,5833333	0,14805
	0,946		-0,06622		1,031	1,22222222	1,1341		0,993	0,6111111	0,14895
11,5	0,947	11,5	-0,06629	11,5	1,028	1,27777778	1,1308	11,5	0,997	0,6388889	0,14955
	0,949		-0,06643		1,024	1,33333333	1,1264		0,997	0,6666667	0,14955
12,5	0,95	12,5	-0,0665	12,5	1,019	1,38888889	1,1209	12,5	0,997	0,6944444	0,14955
	0,95		-0,0665		1,015	1,44444444	1,1165		0,997	0,7222222	0,14955
13,5	0,95	13,5	-0,0665	13,5	1,011	1,5	1,1121	13,5	0,998	0,75	0,1497
	0,952		-0,06664		1,009	1,55555556	1,1099			0,7777778	0,15
14,5	0,954	14,5	-0,06678	14,5	1,008	1,61111111	1,1088	14,5	1,002	0,8055556	0,1503
	0,956		-0,06692		1,007	1,66666667	1,1077		1,005	0,8333333	0,15075
15,5	0,959	15,5	-0,06713	15,5	1,006	1,72222222	1,1066	15,5	1,008	0,8611111	0,1512
	0,961		-0,06727		1,006	1,77777778	1,1066		1,011	0,8888889	0,15165
16,5	0,964	16,5	-0,06748	16,5	1,005	1,83333333	1,1055	16,5	1,011	0,9166667	0,15165
	0,965		-0,06755		1,005	1,88888889	1,1055		1,012	0,9444444	0,1518
17,5	0,966	17,5	-0,06762	17,5	1,003	1,94444444	1,1033	17,5	1,009	0,9722222	0,15135
	0,966		-0,06762		1,002		1,1022		1,008		0,1512
18,5	0,966	18,5	-0,06762	18,5	1,001	2,05555556	1,1011	18,5	1,006	1,0277778	0,1509
	0,967		-0,06769		0,998	2,11111111	1,0978		1,001	1,0555556	0,15015
19,5	0,967	19,5	-0,06769	19,5	0,996	2,16666667	1,0956	19,5	0,998	1,0833333	0,1497
	0,967		-0,06769		0,995	2,22222222	1,0945		0,996	1,1111111	0,1494
20,5	0,968	20,5	-0,06776	20,5	0,994	2,27777778	1,0934	20,5	0,995	1,1388889	0,14925
	0,968		-0,06776		0,994	2,33333333	1,0934		0,995	1,1666667	0,14925
21,5	0,969	21,5	-0,06783	21,5	0,995	2,38888889	1,0945	21,5	0,996	1,1944444	0,1494

Продолжение таблицы 5

Трапеция 4	Трапеция 5
wn=45 Р=-0,18 c=0,5	wn=65 Р=-0,1 c=0,5
0,5	0,24	0,011111	-0,0432	0,5	0,24	0,007692	-0,024
	0,461	0,022222	-0,08298		0,461	0,015385	-0,0461
1,5	0,665	0,033333	-0,1197	1,5	0,665	0,023077	-0,0665
	0,833	0,044444	-0,14994		0,833	0,030769	-0,0833
2,5	0,967	0,055556	-0,17406	2,5	0,967	0,038462	-0,0967
	1,061	0,066667	-0,19098		1,061	0,046154	-0,1061
3,5	1,115	0,077778	-0,2007	3,5	1,115	0,053846	-0,1115
	1,142	0,088889	-0,20556		1,142	0,061538	-0,1142
4,5	1,138	0,1	-0,20484	4,5	1,138	0,069231	-0,1138
	1,118	0,111111	-0,20124		1,118	0,076923	-0,1118
5,5	1,092	0,122222	-0,19656	5,5	1,092	0,084615	-0,1092
	1,051	0,133333	-0,18918		1,051	0,092308	-0,1051
6,5	1,018	0,144444	-0,18324	6,5	1,018	0,1	-0,1018
	0,993	0,155556	-0,17874		0,993	0,107692	-0,0993
7,5	0,974	0,166667	-0,17532	7,5	0,974	0,115385	-0,0974
	0,966	0,177778	-0,17388		0,966	0,123077	-0,0966
8,5	0,966	0,188889	-0,17388	8,5	0,966	0,130769	-0,0966
	0,97	0,2	-0,1746		0,97	0,138462	-0,097
9,5	0,975	0,211111	-0,1755	9,5	0,975	0,146154	-0,0975
	0,982	0,222222	-0,17676		0,982	0,153846	-0,0982
10,5	0,987	0,233333	-0,17766	10,5	0,987	0,161538	-0,0987
	0,993	0,244444	-0,17874		0,993	0,169231	-0,0993
11,5	0,997	0,255556	-0,17946	11,5	0,997	0,176923	-0,0997
	0,997	0,266667	-0,17946		0,997	0,184615	-0,0997
12,5	0,997	0,277778	-0,17946	12,5	0,997	0,192308	-0,0997
	0,997	0,288889	-0,17946		0,997	0,2	-0,0997
13,5	0,998	0,3	-0,17964	13,5	0,998	0,207692	-0,0998
		0,311111	-0,18			0,215385	-0,1
14,5	1,002	0,322222	-0,18036	14,5	1,002	0,223077	-0,1002
	1,005	0,333333	-0,1809		1,005	0,230769	-0,1005
15,5	1,008	0,344444	-0,18144	15,5	1,008	0,238462	-0,1008
	1,011	0,355556	-0,18198		1,011	0,246154	-0,1011
16,5	1,011	0,366667	-0,18198	16,5	1,011	0,253846	-0,1011
	1,012	0,377778	-0,18216		1,012	0,261538	-0,1012
17,5	1,009	0,388889	-0,18162	17,5	1,009	0,269231	-0,1009
	1,008	0,4	-0,18144		1,008	0,276923	-0,1008
18,5	1,006	0,411111	-0,18108	18,5	1,006	0,284615	-0,1006
	1,001	0,422222	-0,18018		1,001	0,292308	-0,1001
19,5	0,998	0,433333	-0,17964	19,5	0,998	0,3	-0,0998
	0,996	0,444444	-0,17928		0,996	0,307692	-0,0996
20,5	0,995	0,455556	-0,1791	20,5	0,995	0,315385	-0,0995
	0,995	0,466667	-0,1791		0,995	0,323077	-0,0995
21,5	0,996	0,477778	-0,17928	21,5	0,996	0,330769	-0,0996

Далее построим графики составляющих переходной характеристики 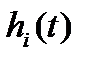. Все составляющие расположим на одном чертеже (рисунок 9) с учетом знака, который определяется знаком высоты 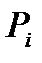соответствующей трапеции.

График переходной характеристики замкнутой системы получим путем суммирования ординат всех составляющих в равные моменты времени

.

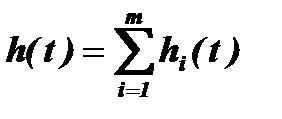t_max t_p

Рисунок 10 – График переходного процесса и его составляющие