Определение коэффициента передачи корректирующего элемента усилителя

Во всех вариантах заданий отсутствуют значения коэффициента передачи корректирующего элемента К_КЭ , включенного в цепь обратной связи усилителя. Не определен также характер обратной связи. В процессе выполнения задания необходимо их определить.

В качестве исходных данных здесь следует использовать ограничения по статической ошибке САР, заданные для каждого технологического процесса как y₀ ± Δ_y .При этом следует помнить, что по определению, статическая ошибка равна разности между установившимся значением контролируемого параметра y_уст и его заданным значением y₀., то есть

Δ_y = y_уст - y₀.

Здесь также рекомендуется использовать связь между передаточной и переходной характеристиками линейной системы с постоянными параметрами, позволяющую утверждать что

К(0) = h(∞).

Значение h(∞) характеризует состояние САР в установившемся режиме, когда все переходные процессы заканчиваются. При t → ∞ контролируемый параметр y → y_уст. Предположив, что р = 0, выражение для передаточной функции САР, изображенной на рис.4.2 , после несложных преобразований можно привести к виду

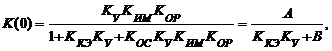
где А = К_У К_ИМ К_ОР , В = 1+К_ОС К_У К_ИМ К_ОР , К_У – известные для каждого варианта параметры элементов САУ.

Если использовать испытательный сигнал в виде y₀ 1(t), то получим переходную характеристику также в виде y₀ h(t). Тгда

y_уст = y₀ К(0) = y₀ h(∞).

Но согласно заданию

y₀ - Δ_y ≤ y_уст≤ y₀ + Δ_y или y₀ - Δ_y ≤ 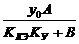≤ y₀ + Δ_y .

В последнем неравенстве неизвестным является параметр К_КЭ , значения которого несложно определить из системы

(y₀ - Δ_y) ( 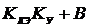) ≤ y₀ А;

(y₀ + Δ_y) ( 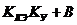) ≥ y₀ А.

В результате решения системы могут получиться значения К_КЭ как положительные, так и отрицательные. Знак «плюс» или «минус» будет означать, соответственно, отрицательную или положительную обратную связь, которую необходимо использовать в усилителе. Этот знак необходимо сохранять при К_КЭ в дальнейших преобразованиях. Величину К_КЭ следует выбрать в интервале найденных значений К_{КЭ мин} < К_КЭ < К_{КЭ макс} , избегая крайних значений. Полученное значение К_КЭ необходимо использовать в выражении (4.2) для передаточной функции САР.

После всех преобразований передаточная функция К(p) должна быть приведена к виду

К(p) 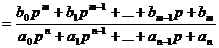, (4.4)

где 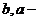постоянные коэффициенты; m и n - целые числа.

Анализ устойчивости системы

Под устойчивостью системы понимают ее способность восстанавливать состояние равновесия после прекращения внешнего воздействия.

Для определения устойчивости САР существуют специальные признаки, называемые критериями устойчивости.

Алгебраический критерий (критерий Гурвица)

Данный критерий основан на анализе коэффициентов характеристического уравнения замкнутой САР

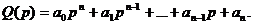(4.5)

Это уравнение получают из формулы (4.4), приравняв ее знаменатель нулю.

Согласно критерию Гурвица САР будет устойчива, если

a₀ > 0 и все диагональные миноры определителя Гурвица больше нуля.

Определитель Гурвица, например, для характеристического уравнения 4-го порядка будет иметь вид:

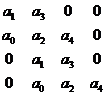(4.6)

САР будет устойчива, если коэффициент a₀ больше нуля и определители третьего и второго порядков также больше нуля:

Δ ₁> 0; Δ ₂ = 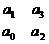= 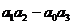> 0;

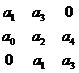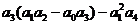Δ ₃ = = > 0;

Δ ₄ = Δ ₃ a₄ > 0.

Частотный критерий (критерий Найквиста)

Этот критерий позволяет определить устойчивость замкнутой САР, используя амплитудно-фазовую характеристику (АФХ) разомкнутой САР. Согласно критерию Найквиста замкнутая САР будет устойчивая, если годограф АФХ разомкнутой системы на комплексной плоскости не охватывает точку с координатами (-1,j0).

Порядок использования критерия Найквиста следующий.

Сначала, путем формальной замены в выражении (4.3) оператора р на jω, получают выражение для АФХ разомкнутой САР в виде

К_Р(jω)= К_П(jω)К_ОС(jω). (4.7)

Затем выражение (4.7) представляют в алгебраической форме, как

К_Р(jω)=Rе{К_Р(jω)}+j·Jm{К_Р(jω)} (4.8)

После этого на комплексной плоскости, при изменении частоты ω от 0 до ∞, строится годограф функции К_Р(jω).

Чтобы представить АФХ в алгебраической форме, необходимо числитель и знаменатель К_Р(jω) домножить на комплексное, сопряженное со знаменателем, число. В знаменателе получим вещественную функцию от частоты ω, а в числителе - функцию от ω, содержащую вещественную и мнимую части.

Для облегчения расчетов при построении годографа можно использовать приемы и правила, основанные на свойствах алгебраических преобразований, таких как:

-модуль дробного комплексного числа равен отношению модуля числителя к модулю знаменателя;

-модуль произведения равен произведению модулей;

-аргумент дробного комплексного числа равен разности аргументов числителя и знаменателя;

-аргумент произведения двух комплексных чисел равен сумме аргументов.