Корреляционно-регрессионные модели.
Корреляционно – регрессионные модели. Постановка задачи – наиболее важный момент в построении корреляционных моделей. От точности поставленной задачи в дальнейшем будет зависеть вся работа. В качестве уточнения постановки задачи проводится теоретический и логический анализ результирующего и определяющего факторов. Здесь определяются границы выборочной совокупности и определяется круг факторов, которые будут исследоваться.
Сбор исходной информации. Самая трудоемкая работа. Исходная информация формируется в виде таблиц, в которых содержатся значения результирующего и определяющих факторов.
После завершения сбора исходной информации приступают к статистической оценке значимости факторов. Статистическая оценка значимости проводится путем расчета коэффициентов парной корреляции. В результате получаются корреляционные матрицы, которые потом подвергаются визуальному анализу.
Таблица 5.1.
Корреляционная матрица
| xij yi | xi1 | xi2 | … | xim |
| y1 | r11 | r12 | … | r1m |
| y2 | r21 | r22 | … | r2m |
| y3 | r31 | r32 | … | r3m |
| … | … | … | … | … |
| yn | rn1 | rn2 | … | rnm |
Следующий шаг - построение эмпирических уравнений регрессии (для определения характера влияния определяющих факторов на результирующий). Для каждого факторного признака Xij на график наносятся точки с координатами (yi, xij)
Затем определяется минимальное и максимальное значение X и Y. Отрезок [xjmin, xjmax] делится на ряд интервалов. В результате получаем:
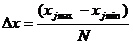, (5.15)
где: N – число интервалов.
Для каждого интервала (∆x) определяется точка со средним значением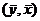 
. Затем на графике эти средние значения соединяются отрезками, мы получаем эмпирическую линию регрессии, при необходимости эта линия регрессии может быть сглажена. В результате получаем некоторую линию, которая отражает характер влияния определяющего фактора на результирующий. Зная характер зависимости, можно выбрать форму сглаживающей кривой. На этом этап предварительной обработки информации заканчивается.
Расчетный этап. Как правило, в социально-экономических исследованиях используют многофакторные модели, но в некоторых случаях полезными являются и однофакторные модели. Однофакторные модели, как правило, строятся при помощи метода наименьших квадратов. Зависимости, которые используются:
- линейная -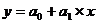 
;
- степенная -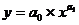 
;
- экспоненциальная -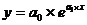 
Следующий шаг – построение многофакторной модели. В качестве основных сглаживающих функций выступают линейные многочлены и мультистепенные функции
Метод расчета – метод наименьших квадратов. Расчеты могут осуществляться в матричной форме. При необходимости в начале проводят процедуру выравнивания.
Затем проводится оценка адекватности и точности построения моделей.
Адекватность полученных моделей, оценивается при помощи нескольких показателей. Полноту учета всех факторов, влияющих на результирующий признак характеризует коэффициент множественной корреляции, он определяется:
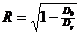, (5.16)
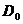– остаточная дисперсия, т.е. это характеристика, которая показывает рассеяние случайной величины 
относительную уравнения регрессии
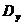- дисперсия 
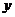относительно среднего значения
Используется коэффициент детерминации – это коэффициент множественной корреляции в квадрате (R ),он показывает долю изменчивости результативного признака за счет всех факторов, включенных в модель. Точность модели можно оценить по средней относительной ошибке.
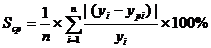(5.17)
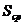показывает на сколько процентов расчетные значения в среднем отклоняются от фактических. Можно рассчитать доверительный интервал, который показывает пределы возможных значений у. Величина доверительного интервала определяется:
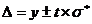(5.18)
где t – доверительная вероятность, которая зависит от уровня риска;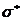 
- среднеквадратическое отклонение i-го расчетного значения у от фактического.
При этом считается, что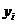 
распределены по нормальному закону с одинаковой дисперсией, а за ее оценку принимается значение остаточной дисперсии.
Для оценки адекватности используются также критерии согласия. Могут использоваться критерии Фишера, Стьюдента, Пирсона и др.