Балансовый метод применяется при изучении соотношения двух групп взаимосвязанных показателей, итоги которых должны быть равны между собой.
Данный способ позволяет выявить в результате новый аналитический (балансирующий) показатель. Используется при анализе обеспеченности предприятия различными видами ресурсов и полноты их использования (баланс рабочего времени, платежный баланс) и т.д. Например, при анализе обеспеченности предприятия сырьем сравнивают потребность в сырье, источники покрытия потребности и определяют балансирующий показатель – дефицит или избыток сырья. Товарно-сырьевой баланс можно представить, как:
| Nн.г. + Nп. = Nр + Nвыб + Nк.г. | (10) |
Каждую составляющую данного баланса можно выразить через алгебраическую сумму других. При анализе необходимо учитывать экономический смысл показателей. Так, прочее выбытие товаров отрицательно влияет на объем реализации.
Как вспомогательный, балансовый метод используется для проверки результатов расчетов влияния факторов на результативный совокупный показатель.
2.3.2 Факторный анализ
Факторный анализ – это метод изучения влияния факторов на результат. Основным результатом детерминированного факторного анализа является разложение прироста результативного показателя, обусловленного совместным влиянием или изменением факторных признаков, на сумму частных приростов результативного показателя, любой из которых обусловлен изменением только одного фактора.
Связь между факторами может быть одного из следующих типов.
Аддитивная связь. Результирующий фактор определяется суммой факторов зависимых, возможно, с некоторыми коэффициентами пропорциональности. Связь описывается следующей формулой:
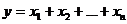 | (11) |
К таким моделям, например, относятся показатели себестоимости во взаимосвязи с элементами затрат на производство и со статьями затрат; показатель объема производства продукции в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в отдельных подразделениях. Например, модель товарного баланса:
| Р = Зн + П - Зк - В | (12) |
где: Р - реализация,
Зн - запасы на начало периода,
П - поступление товаров,
Зк - запасы на конец периода,
В - прочее выбытие товаров.
Мультипликативная связь. Результирующий фактор определяется как произведение факторов зависимых в виде:
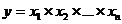 | (13) |
Примером мультипликативной модели является двухфакторная модель объема реализации:
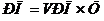 | (14) |
где VРП – объем реализованной продукции в натуральном выражении;
Ц - цена продукции.
Кратная связь. Частное от деления двух факторов дает результирующий фактор.
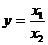 | (15) |
Примером кратной модели служит показатель фондоотдачи:
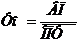 | (16) |
Смешанные модели. Они могут иметь разную форму и представлять собой различные комбинации моделей аддитивных, мультипликативных и кратных, например:
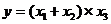 | (17) |
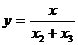 | (18) |
Примерами таких моделей служат показатели затрат на 1 руб. товарной продукции, показатели рентабельности и др. Например, показатель рентабельности активов:
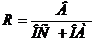 | (19) |
где: В – выручка от реализации;
ОС - стоимость основных средств,
ОА - стоимость оборотных активов.
Моделирование аддитивных систем осуществляется путем расчленения факторов исходной модели на составные элементы.
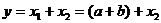 | (20) |
Например, показатель объема реализованной продукции:
| VРП =VВП - Онп | (21) |
где VРП, VВП – объемы реализованной и валовой продукции;
Онп – остатки нереализованной продукции.
Часть нереализованной продукции может находится на складе (Оскл), а часть – отгружена покупателям, но еще не оплачена(Оотг). Тогда исходную модель можно записать:
| VРП =VВП-(Оскл – Оотг) | (22) |
Моделирование мультипликативных моделей осуществляется путем последовательного расчленения факторов исходной системы на факторы –сомножители.
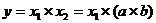 | (23) |
Например, выпуск продукции можно представить следующим образом:
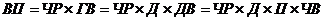 | (24) |
где ВП-выпуск продукции;
ЧР-численность рабочих;
Д-количество дней, отработанных одним рабочим;
П-продолжительность рабочего дня;
ДВ-дневная выработка;
ЧВ-часовая выработка.
Моделирование кратных моделей осуществляется при помощи 3 способов:
Метод удлинения предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей.
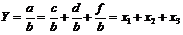 | (25) |
Например, показатель себестоимости продукции можно представить как сумму затрат на весь объем произведенной продукции, деленную на объем произведенной продукции:
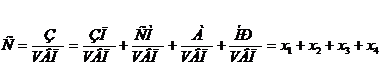 | (26) |
где З - сумма затрат;
VВП –объем выпуска продукции в натуральном выражении;
С, СМ, А,НР – элементы затрат ( заработная плата, сырье и материалы, амортизация и т.д.);
х1 – трудоемкость;
х2 – материалоемкость
х3 – фондоемкость
х4 –уровень накладных расходов.
Метод расширения предусматривает расширение исходной факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей.
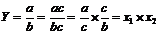 | (27) |
Например, показатель годовой выработки можно представить следующим образом:
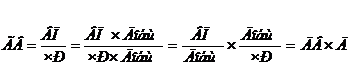 | (28) |
где ГВ - годовая выработка продукции одним рабочим;
ЧР- численность рабочих;
ВП- выпуск продукции;
Добщ – количество отработанных дней всеми работниками;
ДВ - дневная выработка продукции одним рабочим
Д-количество рабочих дней, отработанных одним рабочим.
Метод сокращения осуществляется путем деления дроби на один и тот же показатель.
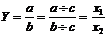 | (29) |
Например, рентабельность активов предприятия можно представить следующим образом:
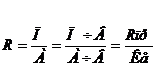 | (30) |
где R –рентабельность активов;
П-прибыль от продаж;
А-сумма активов предприятия;
В-выручка от продаж;
Rпр –рентабельность продаж
Ке – капиталоемкость продукции
Определение величины влияния отдельных факторов на прирост результативных показателей производится при помощи следующих способов: цепной подстановки, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмический, балансовый и т.д.
1. Способ цепной подстановки
Используется для расчета влияния фактов во всех типах детерминированных факторных моделей.
Таблица. Способ цепной подстановки
| Уровень результативного показателя | Условия расчета результативного показателя | |||
| Фактор 1 | Фактор 2 | Фактор 3 | Фактор 4 | |
| Базовый | t0 | t0 | t0 | t0 |
| Условный 1 | t1 | t0 | t0 | t0 |
| Условный 2 | t1 | t1 | t0 | t0 |
| Условный 3 | t1 | t1 | t1 | t0 |
| Фактический | t1 | t1 | t1 | t1 |
Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, двух и последующих факторов, допуская, что остальные не изменяются. Сравнение величины результативного показателя до и после изменения уровня того или иного фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя. Элиминировать – это значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного.
2. Способ абсолютных разниц
Применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе в мультипликативных моделях и мультипликативно – аддитивных. При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста значения исследуемого фактора на базовую величину факторов, которые находятся справа от него, и на фактическую величину факторов, которые находятся слева от него в модели.
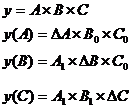 | (31) |
3. Способ относительных разниц
Применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе в мультипликативных моделях. Используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов.
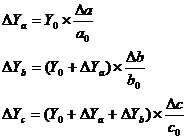 | (32) |
Пример. Провести факторный анализ выпуска продукции
| Показатель | Усл. обоз. | Уровень показателя | Изменение | ||
| Прошлый | Отчетный | Абс. | Отн. | ||
| Валовая продукция, тыс. руб. | ВП | 599,9 | +199,9 | 1,5 | |
| Среднесписочная численность рабочих | ЧР | +20 | 1,2 | ||
| Количество отработанных дней одним рабочим за год | Д | 208,3 | +8,3 | 1,0415 | |
| Средняя продолжительность смены, ч | П | 7,5 | -0,5 | 0,9375 | |
| Среднечасовая выработка продукции одним рабочим, руб. | ЧВ | 2,5 | 3,2 | +0,7 | 1,28 |
Составим мультипликативную факторную модель.
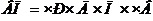 | (33) |
1. Способ цепных подстановок
Подставляем в модель данные прошлого года
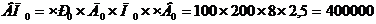
Составляем первую условную модель, меняя первый фактор «Численность рабочих» на отчетный год. Остальные факторы остаются неизменными.
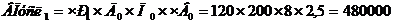
Рассчитываем изменение выпуска продукции, вызванное первым фактором
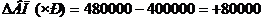
При увеличении численности рабочих на 20 человек выпуск продукции увеличился на 80000 рублей.
Рассчитаем вторую условную модель, меняя второй фактор «Количество отработанных дней» на отчетный год.
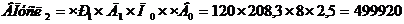
Рассчитываем изменение выпуска продукции, вызванное вторым фактором
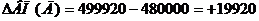
Увеличивая количество отработанных дней до 208,3 дней, выпуск продукции увеличиться на 19920 рублей.
Рассчитаем третью условную модель, меняя третий фактор «Продолжительность рабочего дня» на отчетный год.
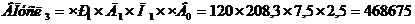
Рассчитываем изменение выпуска продукции, вызванное третьим фактором
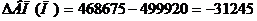
Снижение продолжительности рабочего дня до 7,5 часов, выпуск продукции снизиться на 31245 рублей.
Рассчитаем фактическую модель, меняя последний фактор «Часовая выработка» на отчетный год.
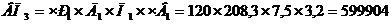
Рассчитываем изменение выпуска продукции, вызванное четвертым фактором
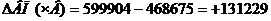
Увеличение часовой выработки привело к росту выпуска продукции на 131229 рублей.
Для оценки общего изменения выпуска продукции можно использовать два способа.
Первый способ. 
Сравнить данные о выпуске продукции отчетного года с прошлым годом.
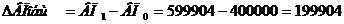
Второй способ. Сложить все частные приросты показателя.
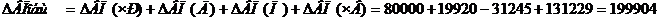Выпуск продукции в целом увеличился в результате влияния всех факторов.
2. Способ абсолютных разниц
Для данного метода используем абсолютное отклонение показателей.
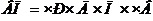
Рассчитываем изменение выпуска продукции в результате изменения первого фактора «Численность рабочих».
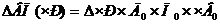
В формулу подставляем абсолютное изменение численности рабочих, а остальные факторы берутся прошлого года, т.к. находятся справа от изучаемого фактора.
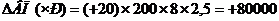
Рассчитываем изменение выпуска продукции в результате изменения второго фактора «Количество отработанных дней».
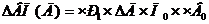
В формулу подставляем абсолютное изменение количества рабочих дней, численность рабочих подставляем за отчетный год, т.к. фактор находится слева от изучаемого, а остальные факторы берутся прошлого года, т.к. находятся справа от изучаемого фактора.
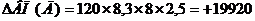
Рассчитываем изменение выпуска продукции в результате изменения третьего фактора «Продолжительность рабочего дня».
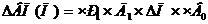
В формулу подставляем абсолютное изменение продолжительности рабочего дня, численность рабочих и количество дней подставляем за отчетный год, т.к. факторы находится слева от изучаемого, а остальные факторы берутся прошлого года, т.к. находятся справа от изучаемого фактора.
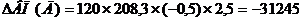
Рассчитываем изменение выпуска продукции в результате изменения четвертого фактора «Часовая выработка».
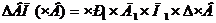
В формулу подставляем абсолютное изменение часовой выработки, факторы подставляем за отчетный год, т.к. они находится слева от изучаемого фактора.
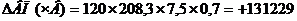
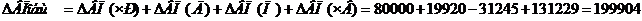
3. Метод относительных разниц
Для данного метода используем абсолютные отклонения результативного фактора и зависимых факторов.
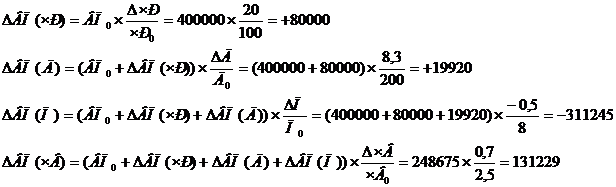
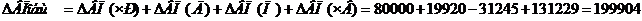
Как видно из расчетов, результаты по всем трем способам совпадают.
4. Метод дифференцирования
Дифференциал - главная линейная часть приращения функции относительно приращения аргументов определяется как
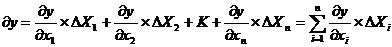 | (34) |
Здесь dy dxi - частная производная функции y по переменной xi, вычисленная в точке А, то есть при x1=x01,x2=x02,...,xn=x0n.
ΔXi - приращение переменной xi при переходе функции из точки А в точку В.
Δx1=x11-x01, Δx2=x12-x02, ......, Δxn=x1n-x0n. Итак, если Δxi→0 (то есть В→А), то Е→0 и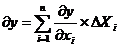 
Влияние изменения фактора xi на изменение показателя y определяется величиной:
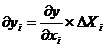 | (35) |
Пример. Выручка, полученная организацией от производства и реализации продукции, может рассчитываться как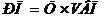 
где VВП - физический объем продукции, ед.
Ц - цена единицы продукции, руб.
В первом квартале реализовано 12 тыс. единиц продукции при средней цене 2400 руб. Показатели второго квартала - 11 тыс. единиц при цене 2500 руб.
Прирост выручки ΔРП ≈ VВП x ΔЦ + Ц x ΔVРП. Точка А здесь I квартал, её координаты А(Ц0, VРП0). Точка В - 2 квартал, В(Ц1, VРП1).
С учетом данных получим А (2400; 12), В(2500;11).
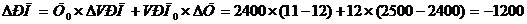тыс. руб.
Итак общее изменение выручки ΔРП= -1200 тыс.руб., в том числе: за счет изменения цены ΔРП(Ц)= +1200 тыс.руб., за счет изменения физического объема ΔРП(VРП) = -2400 тыс.руб.
Если определить прирост показателя РП точно, то получим
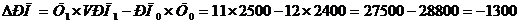тыс. руб.
Видно, что при использовании метода дифференцирования произошла ошибка на 100 тыс.руб. В экономических расчетах, где динамика факторов может быть существенной, значение ошибки может быть большим. Поэтому её нужно учитывать. При этом возникает две задачи:
а) как рассчитать величину этой ошибки?
б) как распределить её между отдельными факторами?
Расчет величины ошибки достаточно прост:
Е= Δy – dy ,
где Δy= y(x11,x12,..., x1n)- y(x01,x02,...,x0n), а значение dy рассчитывается по формуле (35).
Задача распределения величины ошибки (“неразложимого остатка”) между отдельными факторами решается с применением различных методов. Рассмотрим 2 метода.
1)Метод простого прибавления неразложимого остатка заключается в прибавлении величины ошибки Е к приращению показателя, обусловленному динамикой одного из факторов. Наиболее часто для этой цели используется качественный фактор. В этом случае метод дифференцирования обеспечивает такой же результат, как метод цепных подстановок.
Пример. Величина ошибки составила Е= -100 тыс.руб. Качественным фактором является цена. Тогда ΔРПц=1200-100=1100 тыс.руб. Итак: общее изменение выручки ΔРП= -1300 тыс.руб., в том числе: за счет изменения цены ΔРПц= +1100 тыс.руб. за счет изменения физического объема продукции ΔРПvрп= -2400 тыс.руб.
2)Метод деления неразложимого остатка заключается в равном делении величины ошибки Е между всеми факторами.
Пример. На показатель влияют два фактора. Каждый из них скорректируем на Е/2= -50 тыс.руб. Тогда результат анализа будет выглядеть:
Общее изменение выручки ΔВРП= -1300 тыс. руб., в том числе:
за счет изменения цены ΔРПц= +1150 тыс. руб.
за счет изменения физического объема продукции ΔРПм= -2450 тыс. руб.
5. Метод интегрирования
Метод интегрирования является предельным случаем метода дробления приращений факторов при бесконечном увеличении m.
В этом случае
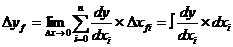 | (36) |
Ошибка разложения при этом отсутствует. Этот метод применяется крайне редко в силу высокой трудоемкости процесса интегрирования.
6. Логарифмический метод
Этот метод используется для показателей, представленных мультипликативными функциями. Рассмотрим его на примере двухфакторной модели П= а∗x. Прологарифмируем её (по любому основанию):
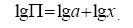 | (37) |
Если значение показателя изменяется с П0 до П1, то разность соответствующих логарифмов можно представить как
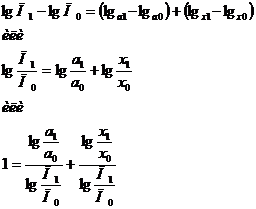 | (38) (39) (40) |
Умножив на ΔП= П1- П0 правую и левую части последнего тождества получим:
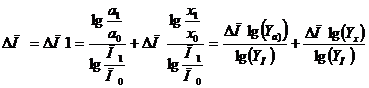 | (41) |
где Υп, Υа, Υx - индексы показателя и факторов.
Здесь первое слагаемое в правой части определяет влияние фактора а на приращение показателя П, а второе - влияние фактора x.
Соответствующие модели могут быть разработаны для любого количества факторов.
Пример. В первом квартале реализовано 12 тыс. единиц продукции при средней цене 2400 руб. Показатели второго квартала - 11 тыс. единиц при цене 2500 руб.
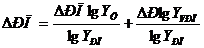
Общее изменение выручки ΔРП= -1300 тыс.руб.,
в том числе: за счет изменения цены ΔРПц= +1138 тыс.руб.;
за счет изменения физического объема продукции ΔРПvрп= -2438 тыс.руб.
2.3.3 Графический метод
Графики представляют собой масштабное изображение показателей, чисел с помощью геометрических знаков (линий, прямоугольников, кругов) или условно-художественных фигур). Основные формы графиков – это диаграммы. По своей форме они бывают столбиковые, полосовые, круговые, квадратные, линейные, фигурные. По содержанию различают диаграммы сравнения, структурные, динамические, графики связи (линейный график), контроля.
Пример. Изобразить графически показатели, представленные в таблице
| Выпуск продукции | 2008 год | 2009 год | Темп роста | Удельный вес, % | |
| 2008 год | 2009 год | ||||
| А | 1,05 | ||||
| Б | 0,93 | ||||
| В | 1,05 | ||||
| Итого | 1,011 |
Представим графически динамику выпуска продукции и структуру.
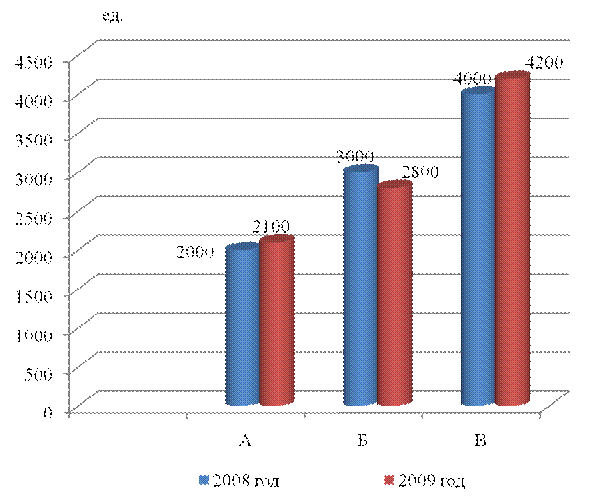
Рисунок. Динамика выпуска продукции
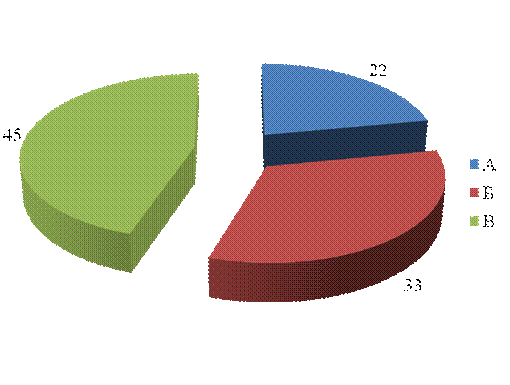
Рисунок. Структура выпуска продукции за 2008 год