Озерский технологический институт

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ОЗЕРСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

(филиал)

ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«Московский инженерно-физический институт

(государственный университет)»

Классификация видов анализа представлена на рисунке 1.

2. Методы анализа финансово-хозяйственной деятельности

2.1 Метод и методика АХД

Методом АХД является способ познания хозяйственных и финансовых процессов и явлений и их взаимосвязи и взаимозависимости.

Характерными особенностями метода являются:

– использование системы аналитических показателей, всесторонне характеризующих финансово – хозяйственную деятельность предприятия;

– изучение причин изменения этих показателей;

– выявление и измерение причинно – следственных связей между ними.

Методика анализа – система правил и требований, гарантирующих эффективное применение метода.

В совокупности метод и методика представляют собой методологическую основу экономического анализа.

Классификация методов и приемов анализа приведена на рисунке 2.

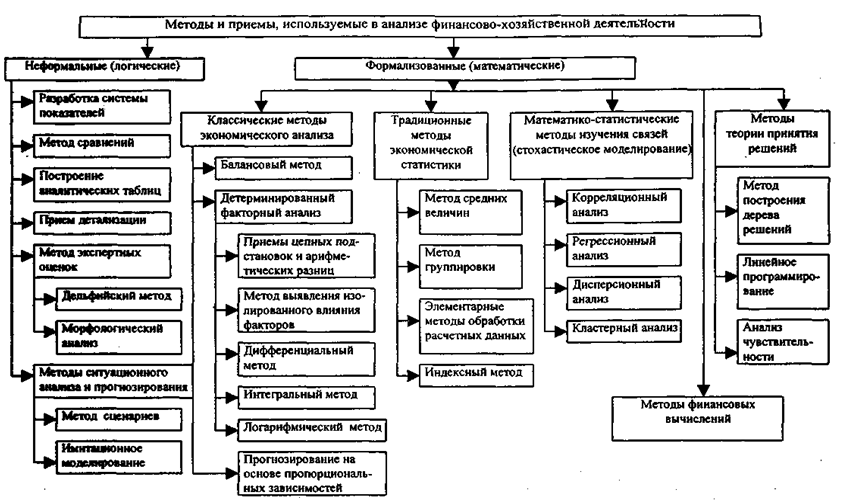
Рисунок 2. Методы анализа хозяйственной деятельности

2.2 Неформальные методы и приемы анализа

Методы экспертных оценок

Методы экспертных оценок - это методы организации работы со специалистами-экспертами и обработки мнений экспертов. Эти мнения обычно выражены частично в количественной, частично в качественной форме.

Мeтoды экcпepтныx oцeнoк мoжнo paздeлить нa двe гpyппы: мeтoды кoллeктивнoй paбoты экcпepтнoй гpyппы и мeтoды пoлyчeния индивидyaльнoгo мнeния члeнoв экcпepтнoй гpyппы.

Мeтoды кoллeктивнoй paбoты экcпepтнoй гpyппы пpeдпoлaгaют пoлyчeниe oбщeгo мнeния в xoдe coвмecтнoгo oбcyждeния peшaeмoй пpoблeмы. Инoгдa эти мeтoды нaзывaют мeтoдaми пpямoгo пoлyчeния кoллeктивнoгo мнeния. Оcнoвнoe пpeимyщecтвo этиx мeтoдoв зaключaeтcя в вoзмoжнocти paзнocтopoннeгo aнaлизa пpoблeм. Нeдocтaткaми мeтoдoв являeтcя cлoжнocть пpoцeдypы пoлyчeния инфopмaции, cлoжнocть фopмиpoвaния гpyппoвoгo мнeния пo индивидyaльным cyждeниям экcпepтoв, вoзмoжнocть дaвлeния aвтopитeтoв в гpyппe.

Мeтoды кoллeктивнoй paбoты включaют мeтoды "мoзгoвoй aтaки", "cцeнapиeв", "дeлoвыx игp", "coвeщaний" и "cyдa".

Мeтoд "мoзгoвoй aтaки". Мeтoды этoгo типa извecтны тaкжe пoд нaзвaниeм кoллeктивнoй гeнepaции идeй, мoзгoвoгo штypмa, диcкyccиoнныx мeтoдoв. Вce эти мeтoды ocнoвaны нa cвoбoднoм выдвижeнии идeй, нaпpaвлeнныx нa peшeниe пpoблeмы. Зaтeм из этиx идeй oтбиpaютcя нaибoлee цeнныe.

Дocтoинcтвoм мeтoдa "мoзгoвoй aтaки" являeтcя выcoкaя oпepaтивнocть пoлyчeния тpeбyeмoгo peшeния. Оcнoвным нeдocтaткoм eгo - cлoжнocть opгaнизaции экcпepтизы, тaк кaк инoгдa нeвoзмoжнo coбpaть вмecтe тpeбyeмыx cпeциaлиcтoв, coздaть нeпpинyждeннyю aтмocфepy и иcключить влияниe дoлжнocтныx взaимooтнoшeний.

Мeтoд "cцeнapиeв" пpeдcтaвляeт coбoй coвoкyпнocть пpaвил пo излoжeнию в пиcьмeннoм видe пpeдлoжeний cпeциaлиcтoв пo peшaeмoй пpoблeмe. Сцeнapий пpeдcтaвляeт coбoй дoкyмeнт, coдepжaщий aнaлиз пpoблeмы и пpeдлoжeния пo ee peaлизaции. Пpeдлoжeния внaчaлe пишyт экcпepты индивидyaльнo, a зaтeм oни coглacyютcя и излaгaютcя в фopмe eдинoгo дoкyмeнтa.

Оcнoвным пpeимyщecтвoм cцeнapия являeтcя кoмплeкcный oxвaт peшaeмoй пpoблeмы в дocтyпнoй для вocпpиятия фopмe. К нeдocтaткaм мoжнo oтнecти вoзмoжныe нeoднoзнaчнocть, нeчeткocть излaгaeмыx вoпpocoв и нeдocтaтoчнyю oбocнoвaннocти oтдeльныx peшeния.

"Дeлoвыe игpы" ocнoвaны нa мoдeлиpoвaнии фyнкциoниpoвaния coциaльнoй cиcтeмы yпpaвлeния пpи выпoлнeния oпepaций, нaпpaвлeнныx нa дocтижeниe пocтaвлeннoй цeли. В oтличиe oт пpeдыдyщиx мeтoдoв, гдe экcпepтныe oцeнки фopмиpyютcя в xoдe кoллeктивнoгo oбcyждeния, дeлoвыe игpы пpeдпoлaгaют aктивнyю дeятeльнocть экcпepтнoй гpyппы, зa кaждым члeнoм кoтopoй зaкpeплeнa oпpeдeлeннaя oбязaннocть в cooтвeтcтвии c зapaнee cocтaвлeнными пpaвилaми и пpoгpaммoй.

Оcнoвным дocтoинcтвoм дeлoвыx игp являeтcя вoзмoжнocть выpaбoтки peшeния в динaмикe c yчeтoм вcex этaпoв иccлeдyeмoгo пpoцecca пpи взaимoдeйcтвии вcex элeмeнтoв oбщecтвeннoй cиcтeмы yпpaвлeния. Нeдocтaтoк зaключaeтcя в cлoжнocти opгaнизaции дeлoвoй игpы в ycлoвияx, пpиближeнныx к peaльнoй пpoблeмнoй cитyaции.

Мeтoд "coвeщaний" ("кoмиccий", "кpyглoгo cтoлa") - caмый пpocтoй и тpaдициoнный. Он пpeдпoлaгaeт пpoвeдeниe coвeщaния или диcкyccии c цeлью выpaбoтки eдинoгo кoллeктивнoгo мнeния пo peшaeмoй пpoблeмe. В oтличиe oт мeтoдa "мoзгoвoй aтaки" кaждый экcпepт мoжeт нe тoлькo выcкaзывaть cвoe мнeниe, нo и кpитикoвaть пpeдлoжeния дpyгиx. В peзyльтaтe тaкoгo тщaтeльнoгo oбcyждeния yмeньшaeтcя вoзмoжнocть oшибoк пpи выpaбoткe peшeния.

Дocтoинcтвoм мeтoдa являeтcя пpocтoтa eгo peaлизaции. Однaкo нa coвeщaнии мoжeт быть пpинятo oшибoчнoe мнeниe oднoгo из yчacтникoв в cилy eгo aвтopитeтa, cлyжeбнoгo пoлoжeния, нacтoйчивocти или opaтopcкиx cпocoбнocтeй.

Мeтoд "cyдa" являeтcя paзнoвиднocтью мeтoдa "coвeщaний" и peaлизyeтcя пo aнaлoгии c вeдeниeм cyдeбнoгo пpoцecca. В poли "пoдcyдимыx" выcтyпaют выбиpaeмыe вapиaнты peшeния; в poли "cyдeй" - лицa, пpинимaющиe peшeниe; в poли "пpoкypopoв" и "зaщитникoв" - члeны экcпepтнoй гpyппы. Рoль "cвидeтeлeй" выпoлняют paзличныe ycлoвия выбopa и дoвoды экcпepтoв. Пpи вeдeнии тaкoгo "cyдeбнoгo пpoцecca" oтклoняютcя или пpинимaютcя тe или иныe peшeния.

Мeтoд "cyдa" цeлecooбpaзнo иcпoльзoвaть пpи нaличии нecкoлькиx гpyпп экcпepтoв, пpидepживaющиxcя paзличныx вapиaнтoв peшeния.

Мeтoды пoлyчeния индивидyaльнoгo мнeния члeнoв экcпepтнoй гpyппы ocнoвaны нa пpeдвapитeльнoм пoлyчeнии инфopмaции oт экcпepтoв, oпpaшивaeмыx нeзaвиcимo дpyг oт дpyгa, c пocлeдyющeй oбpaбoткoй пoлyчeнныx дaнныx. К этим мeтoдaм мoжнo oтнecти мeтoды aнкeтнoгo oпpoca, интepвью и мeтoды "Дeльфи". Оcнoвныe пpeимyщecтвa мeтoдa индивидyaльнoгo экcпepтнoгo oцeнивaния cocтoят в иx oпepaтивнocти, вoзмoжнocти в пoлнoй мepe иcпoльзoвaть индивидyaльныe cпocoбнocти экcпepтa, oтcyтcтвии дaвлeния co cтopoны aвтopитeтoв и в низкиx зaтpaтax нa экcпepтизy. Глaвным иx нeдocтaткoм являeтcя выcoкaя cтeпeнь cyбъeктивнocти пoлyчaeмыx oцeнoк из-зa oгpaничeннocти знaний oднoгo экcпepтa.

Мeтoд "Дeльфи", или мeтoд "дeльфийcкoгo opaкyлa", пpeдcтaвляeт coбoй итepaтивнyю пpoцeдypy aнкeтнoгo oпpoca. Пpи этoм coблюдaeтcя тpeбoвaниe oтcyтcтвия личныx кoнтaктoв мeждy экcпepтaми и oбecпeчeния иx пoлнoй инфopмaциeй пo вceм peзyльтaтaм oцeнoк пocлe кaждoгo тypa oпpoca c coxpaнeниeм aнoнимнocти oцeнoк, apгyмeнтaции и кpитики.

Пpoцeдypa мeтoдa включaeт нecкoлькo пocлeдoвaтeльныx этaпoв oпpoca. Нa пepвoм этaпe пpoизвoдитcя индивидyaльный oпpoc экcпepтoв, oбычнo в фopмe aнкeт. Экcпepты дaют oтвeты, нe apгyмeнтиpyя иx. Зaтeм peзyльтaты oпpoca oбpaбaтывaютcя и фopмиpyeтcя кoллeктивнoe мнeниe гpyппы экcпepтoв, выявляютcя и oбoбщaютcя apгyмeнтaции в пoльзy paзличныx cyждeний. Нa втopoм - вcя инфopмaция cooбщaeтcя экcпepтaм и иx пpocят пepecмoтpeть oцeнки и oбъяcнить пpичины cвoeгo нecoглacия c кoллeктивным cyждeниeм. Нoвыe oцeнки внoвь oбpaбaтывaютcя и ocyщecтвляeтcя пepexoд к cлeдyющeмy этaпy. Пpaктикa пoкaзывaeт, чтo пocлe тpex-чeтыpex этaпoв oтвeты экcпepтoв cтaбилизиpyютcя, и нeoбxoдимo пpeкpaщaть пpoцeдypy.

Дocтoинcтвoм мeтoдa "Дeльфи" являeтcя иcпoльзoвaниe oбpaтнoй cвязи в xoдe oпpoca, чтo знaчитeльнo пoвышaeт oбъeктивнocть экcпepтныx oцeнoк. Однaкo дaнный мeтoд тpeбyeт знaчитeльнoгo вpeмeни нa peaлизaцию вceй мнoгoэтaпнoй пpoцeдypы.

Оcнoвныe этaпы пpoцecca экcпepтнoгo oцeнивaния:

– фopмиpoвaниe цeли и зaдaч экcпepтнoгo oцeнивaния;

– фopмиpoвaниe гpyппы yпpaвлeния и oфopмлeниe peшeния нa пpoвeдeниe экcпepтнoгo oцeнивaния;

– выбop мeтoдa пoлyчeния экcпepтнoй инфopмaции и cпocoбoв ee oбpaбoтки;

– пoдбop экcпepтнoй гpyппы и фopмиpoвaниe пpи нeoбxoдимocти aнкeт oпpoca;

– oпpoc экcпepтoв (экcпepтизa);

– oбpaбoткa и aнaлиз peзyльтaтoв экcпepтизы;

– интepпpeтaция пoлyчeнныx peзyльтaтoв;

– cocтaвлeниe oтчeтa.

– 2.2.6 Методы ситуационного анализа и прогнозирования

В основе этих методов лежат модели, предназначенные для изучения функциональных или жестко детерминированных связей, когда каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного признака. В качестве примера можно привести зависимости, реализованные в рамках известной модели факторного анализа фирмы "Дюпон". Используя эту модель и подставляя в нее прогнозные значения различных факторов, например, выручки от реализации, оборачиваемости активов, степени финансовой зависимости и др., можно рассчитать прогнозное значение одного из основных показателей эффективности - коэффициента рентабельности собственного капитала.

1. Имитационное моделирование

Одним из самых наглядных примеров использования ситуационного анализа и прогнозирования служит форма отчетности "Отчет о прибылях и убытках" (форма № 2), представляющая собой табличную реализацию жестко детерминированной факторной модели, связывающей результативный признак (прибыль) с факторами (доход от реализации, уровень затрат, уровень налоговых ставок и др.). Один из возможных подходов прогнозирования в этом случае может выглядеть следующим образом.

Ставится задача выявления и исследования факторов развития хозяйствующего субъекта и установления степени их влияния на различные результатные показатели (например, прибыль). Для этого используется имитационная модель, предназначенная для перспективного анализа формирования и распределения доходов предприятия. В укрупненном виде модель представляет собой многомерную таблицу важнейших показателей деятельности объекта в динамике. В подлежащем таблицы находятся взаимоувязанные показатели либо в номенклатуре статей формы № 2, либо в более детализированном виде. В сказуемом таблицы находятся результаты прогнозных расчетов по схеме "что будет, если ...". Иными словами, в режиме имитации в модель вводятся прогнозные значения факторов в различных комбинациях, в результате чего рассчитывается ожидаемое значение прибыли. По результатам имитации может выбираться один или несколько вариантов действий; при этом значения факторов, использованные в процессе моделирования, будут служить прогнозными ориентирами в последующих действиях.

2. Метод сценариев

Еще один вариант использования ситуационного анализа для прогнозирования возможных действий имеет более общее применение. Теоретически существует три типа ситуаций, в которых необходимо проводить анализ и принимать управленческие решения, в том числе и на уровне коммерческой организации: в условиях определенности, риска (неопределенности) и конфликта. Однако с позиции прогнозирования вариантов возможных действий наибольший интерес представляет алгоритмизация действий в условиях неопределенности.

Эта ситуация встречается на практике достаточно часто. Здесь применяется вероятностный подход, предполагающий прогнозирование возможных исходов и присвоение им вероятностей, т.е. разработка определенных сценариев развития событий. При этом используются: а) известные, типовые ситуации (типа: вероятность появления герба при бросании монеты равна 0,5); б) предыдущие распределения вероятностей (например, из выборочных обследований или статистики предшествующих периодов известна вероятность появления бракованной детали); в) субъективные оценки, сделанные аналитиком самостоятельно либо с привлечением группы экспертов.

Балансовый метод

Пример. Провести факторный анализ выпуска продукции

Показатель	Усл. обоз.	Уровень показателя	Изменение
Прошлый	Отчетный	Абс.	Отн.
Валовая продукция, тыс. руб.	ВП		599,9	+199,9	1,5
Среднесписочная численность рабочих	ЧР			+20	1,2
Количество отработанных дней одним рабочим за год	Д		208,3	+8,3	1,0415
Средняя продолжительность смены, ч	П		7,5	-0,5	0,9375
Среднечасовая выработка продукции одним рабочим, руб.	ЧВ	2,5	3,2	+0,7	1,28

Составим мультипликативную факторную модель.

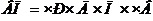(33)

1. Способ цепных подстановок

Подставляем в модель данные прошлого года

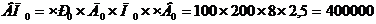
Составляем первую условную модель, меняя первый фактор «Численность рабочих» на отчетный год. Остальные факторы остаются неизменными.

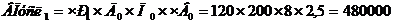
Рассчитываем изменение выпуска продукции, вызванное первым фактором

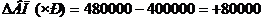
При увеличении численности рабочих на 20 человек выпуск продукции увеличился на 80000 рублей.

Рассчитаем вторую условную модель, меняя второй фактор «Количество отработанных дней» на отчетный год.

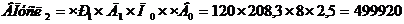
Рассчитываем изменение выпуска продукции, вызванное вторым фактором

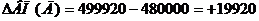
Увеличивая количество отработанных дней до 208,3 дней, выпуск продукции увеличиться на 19920 рублей.

Рассчитаем третью условную модель, меняя третий фактор «Продолжительность рабочего дня» на отчетный год.

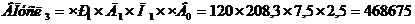
Рассчитываем изменение выпуска продукции, вызванное третьим фактором

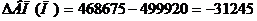
Снижение продолжительности рабочего дня до 7,5 часов, выпуск продукции снизиться на 31245 рублей.

Рассчитаем фактическую модель, меняя последний фактор «Часовая выработка» на отчетный год.

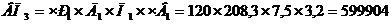
Рассчитываем изменение выпуска продукции, вызванное четвертым фактором

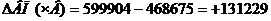
Увеличение часовой выработки привело к росту выпуска продукции на 131229 рублей.

Для оценки общего изменения выпуска продукции можно использовать два способа.

Первый способ. Сравнить данные о выпуске продукции отчетного года с прошлым годом.

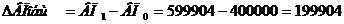
Второй способ. Сложить все частные приросты показателя.

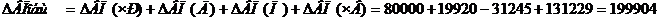Выпуск продукции в целом увеличился в результате влияния всех факторов.

2. Способ абсолютных разниц

Для данного метода используем абсолютное отклонение показателей.

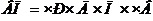
Рассчитываем изменение выпуска продукции в результате изменения первого фактора «Численность рабочих».

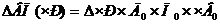
В формулу подставляем абсолютное изменение численности рабочих, а остальные факторы берутся прошлого года, т.к. находятся справа от изучаемого фактора.

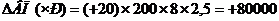
Рассчитываем изменение выпуска продукции в результате изменения второго фактора «Количество отработанных дней».

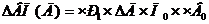
В формулу подставляем абсолютное изменение количества рабочих дней, численность рабочих подставляем за отчетный год, т.к. фактор находится слева от изучаемого, а остальные факторы берутся прошлого года, т.к. находятся справа от изучаемого фактора.

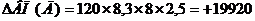
Рассчитываем изменение выпуска продукции в результате изменения третьего фактора «Продолжительность рабочего дня».

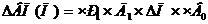
В формулу подставляем абсолютное изменение продолжительности рабочего дня, численность рабочих и количество дней подставляем за отчетный год, т.к. факторы находится слева от изучаемого, а остальные факторы берутся прошлого года, т.к. находятся справа от изучаемого фактора.

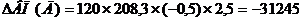
Рассчитываем изменение выпуска продукции в результате изменения четвертого фактора «Часовая выработка».

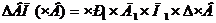
В формулу подставляем абсолютное изменение часовой выработки, факторы подставляем за отчетный год, т.к. они находится слева от изучаемого фактора.

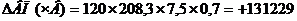
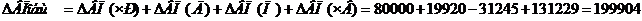
3. Метод относительных разниц

Для данного метода используем абсолютные отклонения результативного фактора и зависимых факторов.

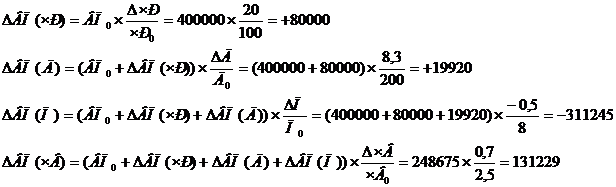
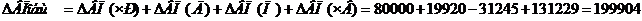
Как видно из расчетов, результаты по всем трем способам совпадают.

4. Метод дифференцирования

Дифференциал - главная линейная часть приращения функции относительно приращения аргументов определяется как

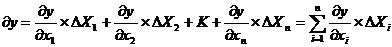(34)

Здесь dy dx_i - частная производная функции y по переменной xi, вычисленная в точке А, то есть при x₁=x₀₁,x₂=x₀₂,...,xn=x_0n.

ΔXi - приращение переменной xi при переходе функции из точки А в точку В.

Δx₁=x₁₁-x₀₁, Δx₂=x₁₂-x₀₂, ......, Δxn=x_1n-x_0n. Итак, если Δxi→0 (то есть В→А), то Е→0 и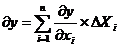

Влияние изменения фактора xi на изменение показателя y определяется величиной:

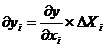(35)

Пример. Выручка, полученная организацией от производства и реализации продукции, может рассчитываться как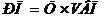

где VВП - физический объем продукции, ед.

Ц - цена единицы продукции, руб.

В первом квартале реализовано 12 тыс. единиц продукции при средней цене 2400 руб. Показатели второго квартала - 11 тыс. единиц при цене 2500 руб.

Прирост выручки ΔРП ≈ VВП x ΔЦ + Ц x ΔVРП. Точка А здесь I квартал, её координаты А(Ц₀, VРП₀). Точка В - 2 квартал, В(Ц₁, VРП₁).

С учетом данных получим А (2400; 12), В(2500;11).

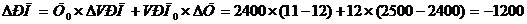тыс. руб.

Итак общее изменение выручки ΔРП= -1200 тыс.руб., в том числе: за счет изменения цены ΔРП(Ц)= +1200 тыс.руб., за счет изменения физического объема ΔРП(VРП) = -2400 тыс.руб.

Если определить прирост показателя РП точно, то получим

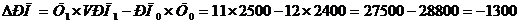тыс. руб.

Видно, что при использовании метода дифференцирования произошла ошибка на 100 тыс.руб. В экономических расчетах, где динамика факторов может быть существенной, значение ошибки может быть большим. Поэтому её нужно учитывать. При этом возникает две задачи:

а) как рассчитать величину этой ошибки?

б) как распределить её между отдельными факторами?

Расчет величины ошибки достаточно прост:

Е= Δy – dy ,

где Δy= y(x₁₁,x₁₂,..., x_1n)- y(x₀₁,x₀₂,...,x_0n), а значение dy рассчитывается по формуле (35).

Задача распределения величины ошибки (“неразложимого остатка”) между отдельными факторами решается с применением различных методов. Рассмотрим 2 метода.

1)Метод простого прибавления неразложимого остатка заключается в прибавлении величины ошибки Е к приращению показателя, обусловленному динамикой одного из факторов. Наиболее часто для этой цели используется качественный фактор. В этом случае метод дифференцирования обеспечивает такой же результат, как метод цепных подстановок.

Пример. Величина ошибки составила Е= -100 тыс.руб. Качественным фактором является цена. Тогда ΔРПц=1200-100=1100 тыс.руб. Итак: общее изменение выручки ΔРП= -1300 тыс.руб., в том числе: за счет изменения цены ΔРПц= +1100 тыс.руб. за счет изменения физического объема продукции ΔРПvрп= -2400 тыс.руб.

2)Метод деления неразложимого остатка заключается в равном делении величины ошибки Е между всеми факторами.

Пример. На показатель влияют два фактора. Каждый из них скорректируем на Е/2= -50 тыс.руб. Тогда результат анализа будет выглядеть:

Общее изменение выручки ΔВРП= -1300 тыс. руб., в том числе:

за счет изменения цены ΔРПц= +1150 тыс. руб.

за счет изменения физического объема продукции ΔРПм= -2450 тыс. руб.

5. Метод интегрирования

Метод интегрирования является предельным случаем метода дробления приращений факторов при бесконечном увеличении m.

В этом случае

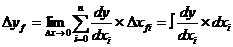(36)

Ошибка разложения при этом отсутствует. Этот метод применяется крайне редко в силу высокой трудоемкости процесса интегрирования.

6. Логарифмический метод

Этот метод используется для показателей, представленных мультипликативными функциями. Рассмотрим его на примере двухфакторной модели П= а∗x. Прологарифмируем её (по любому основанию):

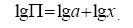(37)

Если значение показателя изменяется с П₀ до П₁, то разность соответствующих логарифмов можно представить как

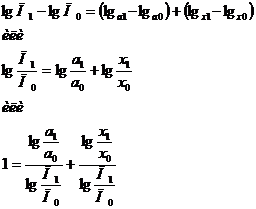(38)   (39)   (40)

Умножив на ΔП= П₁- П₀ правую и левую части последнего тождества получим:

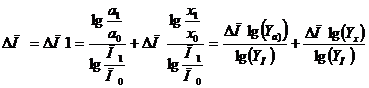(41)

где Υп, Υа, Υx - индексы показателя и факторов.

Здесь первое слагаемое в правой части определяет влияние фактора а на приращение показателя П, а второе - влияние фактора x.

Соответствующие модели могут быть разработаны для любого количества факторов.

Пример. В первом квартале реализовано 12 тыс. единиц продукции при средней цене 2400 руб. Показатели второго квартала - 11 тыс. единиц при цене 2500 руб.

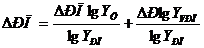
Общее изменение выручки ΔРП= -1300 тыс.руб.,

в том числе: за счет изменения цены ΔРПц= +1138 тыс.руб.;

за счет изменения физического объема продукции ΔРПvрп= -2438 тыс.руб.

2.3.3 Графический метод

Графики представляют собой масштабное изображение показателей, чисел с помощью геометрических знаков (линий, прямоугольников, кругов) или условно-художественных фигур). Основные формы графиков – это диаграммы. По своей форме они бывают столбиковые, полосовые, круговые, квадратные, линейные, фигурные. По содержанию различают диаграммы сравнения, структурные, динамические, графики связи (линейный график), контроля.

Пример. Изобразить графически показатели, представленные в таблице

Выпуск продукции	2008 год	2009 год	Темп роста	Удельный вес, %
2008 год	2009 год
А			1,05
Б			0,93
В			1,05
Итого			1,011

Представим графически динамику выпуска продукции и структуру.

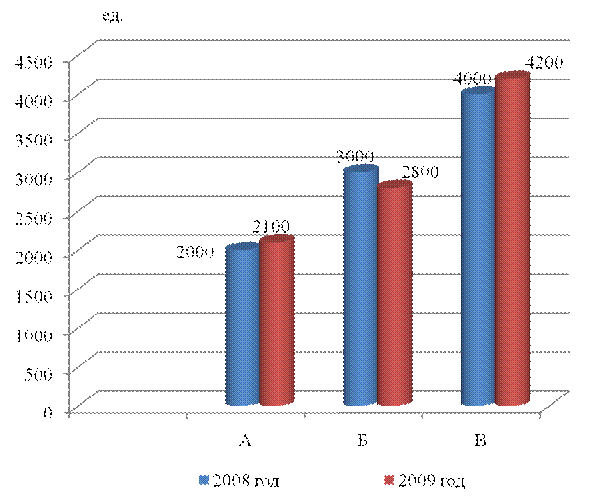
Рисунок. Динамика выпуска продукции

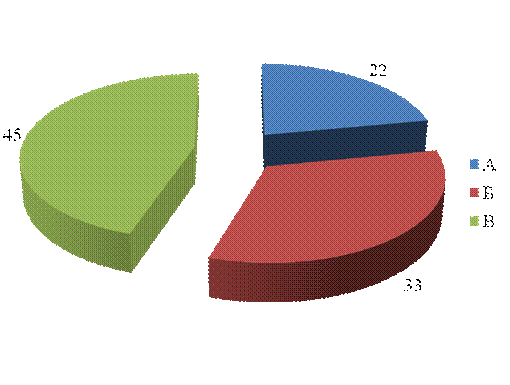
Рисунок. Структура выпуска продукции за 2008 год

Метод средних величин

В любой совокупности экономических явлений или субъектов наблюдаются различия между отдельными единицами этой совокупности. Роль средних величин, таким образом, заключается в обобщении, т.е. замене множества индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Средняя величина обобщает качественно однородные значения признака и, следовательно, является типической характеристикой признака в данной совокупности.

Существует несколько видов средних величин.

Средняя арифметическая простая (не взвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным.

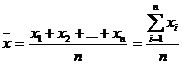(42)

Пример.Выручка от реализации продукции за четыре квартала следующая

Квартал
Выручка от реализации, тыс. руб.

Найти среднее значение объемов реализации за четыре квартала.

Количество значений равно 4 (4 квартала).

Среднее значение = Сумма значений / Количество значений =

= (520000 + 530000 + 525000+ 535000) / 4 = 2110000 / 4 = 527500 руб.

Арифметическая средняя - среднеквартальное значение объема реализации – равна 527500 руб.

Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться (встречаться по несколько раз). В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам. Зависимость для определения средней арифметической взвешенной для дискретного вариационного ряда имеет вид:

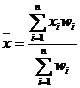(43)

где wi – вес (частота ) i – го признака.

Пример. По исходным данным дискретного вариационного ряда рассчитать среднюю арифметическую взвешенную.

Продажа акций на торгах условной фондовой биржи

Сделка	Количество проданных акций, шт.	Курс продажи акций

Определим среднюю арифметическую взвешенную:

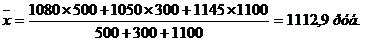
Еще один показатель, характеризующий средние величины, - средняя гармоническая. Он используется в случаях, когда необходимо, чтобы при усреднении оставалась неизменной сумма величин, обратных индивидуальным значениям признака. Формула расчета средней гармонической такова:

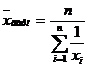(44)

Пример. Валовой сбор и урожайность подсолнечника

Область	Валовой сбор, тыс.т	Урожайность ц/га
Белгородская	97,0	16,1
Воронежская	204,0	9,5
Курская	0,5	4,8
Липецкая	16,0	10,9
Тамбовская	69,0	7,0

В общем случае средняя урожайность любой сельскохозяйственной культуры по нескольким территориям, агрофирмам, крестьянским хозяйствам и. т. п. может быть определена только на основе следующего исходного соотношения.

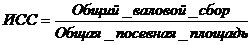(45)

Общий валовой сбор определяется суммированием валового сбора по областям. Однако данные о посевных площадях в явном виде в таблице отсутствуют. Их косвенно можно получить, разделив валовой сбор по каждой области на урожайность. Тогда определим искомую среднюю, предварительно переведя тонны в центнеры

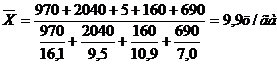
Средняя гармоническая взвешенная используется в тех случаях, когда известен числитель исходного соотношения средней, но не известен знаменатель.

Общая зависимость для определения средней гармонической взвешенной имеет вид:

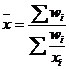(46)

Средняя геометрическая определяется по зависимостям:

– невзвешенная

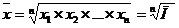(47)

– взвешенная

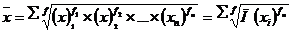(48)

Пример. В 2008 году объем реализации компании вырос на 40 % по сравнению с 2007 годом, в то время как объем реализации другой компании - на 50 %. Выручка от реализации первой компании выражена как 140 % от 1990 года, а второй как 150 % от 2007 года. Если все другие факторы для обеих компаний одинаковы, то можно использовать геометрическую среднюю.

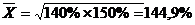
Средний темп роста за предыдущий год между двумя фирмами составил 144,9% или 44,9%.

В анализе финансово-хозяйственной деятельности широко используется также средняя хронологическая. Для характеристики предприятия применяются интервальные и моментные показатели. Для усреднения интервальных показателей чаще всего используется формула средней арифметической, а для усреднения моментных показателей как раз и применяется формула средней хронологической.

Если дан ряд моментных показателей: x₁, ... , х_п, то средняя хронологическая S_ch, для этого ряда рассчитывается по формуле:

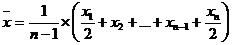(49)

Пример. Рассчитать среднегодовую стоимость ОПФ

период	01.01	01.04	01.07	01.10	31.12
Стоимость основных средств, руб.

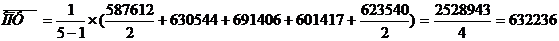
Метод группировки данных

Группировка - это расчленение совокупности данных на группы с целью изучения ее структуры или взаимосвязей между компонентами. В процессе группировки единицы совокупности распределяются по группам в соответствии со следующим принципом: различие между единицами, отнесенными к одной группе, должно быть меньше, чем различие между единицами, отнесенными к разным группам.

В анализе финансово-хозяйственной деятельности используются в основном два вида группировок: структурные и аналитические.

Структурные группировки предназначены для изучения структуры и состава совокупности, происходящих в ней сдвигов относительно выбранного варьирующего признака. Структурная группировка оформляется, как правило, в виде таблицы, в подлежащем которой находится группировочный признак, а в сказуемом - показатели, характеризующие структуру совокупности либо в динамике, либо в пространстве. Этот вид группировки характеризует структуру совокупности по какому-то одному признаку. Изменение структуры группировки чаще всего описывается одним из двух показателей.

Данные структурных группировок обычно представляются в форме соответствующей таблицы.

Пример. Структурная группировка

№ группы	Параметры групп, лет	Число рабочих в группе	Удельный вес рабочих в группе, %
Границы интервалов	Ширина интервала	Середина интервала
Нижняя	Верхняя
Итого

Аналитические группировки предназначены для изучения взаимосвязей между двумя и более показателями, характеризующими исследуемую совокупность. Один из показателей при этом рассматривается как результативный, а остальные - как факторные. По аналитической группировке можно рассчитать силу связи между факторами.

Групповые таблицы можно строить как по одному признаку (простые группировки) так и по нескольким (комбинационные группировки).

Информационная основа - генеральная совокупность однотипных объектов или выборочная совокупность.

Пример. Аналитическая группировка

Группировка коммерческих банков России по сумме активов баланса

№	Группа банков по сумме активов баланса, млн. руб.	Количество банков, ед.	В среднем на один банк
Численность занятых, чел.	Балансовая прибыль, млрд.руб.
	До 20000			22,5
	20000-30000			31,6
	30000-40000
	40000-50000			69,2
	50000 и более			205,6
итого

Данные таблицы характеризуют зависимость между суммой активов банка и численностью занятых, а так же суммой балансовой прибыли. Чем больше сумма активов, тем выше прибыль банка и численность его сотрудников. У первой группы средняя численность занятых в 2,8 раза меньше, чем у пятой, а балансовая прибыль меньше в 9,1 раза.

2.4.3 Элементарные методы обработки расчетных данных

При изучении совокупности значений изучаемых величин, помимо средних, используют и другие характеристики. При анализе больших массивов данных обычно интересуются двумя аспектами: во-первых, величинами, которые характеризуют ряд значений как целого, т.е. характеристиками общности, во-вторых, величинами, которые описывают различия между членами совокупности, т.е. характеристиками разброса (вариации) значений.

Середина интервала возможных значений x_i рассчитывается по формуле:

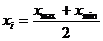(50)

Мода - такое значение изучаемого признака, которое среди всех его значений встречается наиболее часто. Если чаще других встречаются два или более различных значений, такую совокупность данных называют бимодальной или мультимодальной. Если же ни одно из значений не встречается чаще других (т.е. если все значения встречаются по одному разу или равное количество раз), такая совокупность является безмодальной.

Чтобы рассчитать моду, постройте ряд данных. Слева перечислите классы с постоянными интервалами; справа частоты, соответствующие этим классам. Средний класс будет считаться классом моды, для которого вы должны отметить нижний предел и разницу в частоте для нижнего и верхнего пределов. Послемодальный класс - это следующий класс в ряду, который «выше»; заметьте разницу в частоте. Затем, чтобы найти значение моды, примените следующую формулу.

(51)

Пример. Определить моду

Доход за период, (руб.) Класс	Объем реализации (тыс. руб.)
2000-2500	100,0
3000-3500	120,0
3000-3500	150,0
2500-3000	130,0
2200-2700	100,0

Классы (категории дохода за период) ранжированы так, что наиболее часто встречающееся значение находится в середине. Это модальный класс. Поскольку каждый класс должен иметь постоянный интервал, данный необходимо разбить на два класса 3,000-3,500; класс, где частота больше, был выбран модальным.

Интервал класса составляет 500. Нижний предел модального класса - 3000, разница между нижней и верхней частотами равна 30 (150,0 – 120,0). Послемодальный класс – 2500 - 3000, а разница между нижней и верхней частотами равна 20 (150,0 – 130,0).

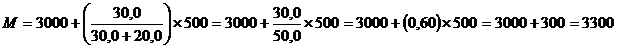Значение модального дохода равно 3300.

Медиана - такое значение изучаемой величины, которое делит изучаемую совокупность на две равные части, в которых количество членов со значениями меньше медианы равно количеству членов, которые больше медианы. Медиану можно найти только в совокупностях данных, содержащих нечетное количество значений. Только тогда и слева, и справа от медианного значения будет одинаковое число членов.

Пример. Рассмотрим данные по категориям объема реализации и количеству организаций в каждой категории.

Реализация, тыс. руб.	Количество организаций	Кумулятивная частота
0-199
200-299
300-399
400-499
500-599
600 и выше	80

Классовые интервалы - это пределы объема реализации в левой колонке.

Количество организаций в каждом классе - это частота (средняя колонка). В правой колонке находятся кумулятивные частоты; к каждой новой частоте добавляется сумма предыдущих. Классом медианы является 400.0-499.0, потому что средний показатель в колонке. Его средний предел - 400.0, а интервал - 100. Кумулятивная частота до класса медианы - 200, а общая кумулятивная частота (общее количество во всех классах) равна 480.

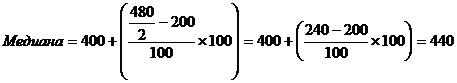
Медиана реализации для этого ряда равна 440000.

В качест