Учебное пособие «Финансовая математика»

Н.В. Коптева, С.П. Семенов

Учебное пособие «Финансовая математика»

Н.В. Коптева, С.П. Семенов

Учебное пособие
«Финансовая математика»

Год издания: 2003

Издатель: Издательство Алтайского госуниверситета

Аннотация

Подготовлено при содействии НФПК – Национального фонда подготовки кадров в рамках Программы "Совершенствование преподавания социально-экономических дисциплин в вузах" Инновационного проекта развития образования. Предназначен для бакалавров-экономистов.

Учебное пособие содержит систематизированное изложение основных понятий и методов финансовых вычислений и количественного анализа финансовых операций. Содержание курса охватывает: базовые разделы финансовой математики; а также построение плана погашения кредита и финансовый анализ инвестиций. Базовые разделы финансовой математики и опирающиеся на них прикладные финансовые расчеты сопровождаются использованием технологии табличного процессора Excel.

Пособие предназначено для бакалавров направлений "Экономика" и "Прикладная математика". Возможно использование учебного курса для слушателей факультетов повышения квалификации экономических специальностей, а также для экономистов-практиков.

Учебный курс разработан при поддержке Национального фонда подготовки кадров в рамках Программы "Совершенствование социально-экономического образования в вузах".

Оглавление

Предисловие

Часть 1. Теоретические основы финансово-коммерческих вычислений

1. Глава

1.1. Фактор времени в финансово-коммерческих расчетах

1.2. Сущность финансовой математики

1.3. Основные категории, используемые в финансово-экономических расчетах

test1. Тесты для проверки усвоения пройденного материала

Глава 2. Операции наращения

2.1. Простые проценты

2.1.1. Формула простых процентов

2.1.2. Расчет процентов с использование процентных чисел

2.1.3. Переменные ставки

2.1.4. Определение срока ссуды и величины процентной ставки.

2.2. Сложные проценты

2.2.1. Формула сложных процентов

2.2.2. Эффективная ставка процентов

2.2.3. Переменная ставка процентов

2.2.4. Непрерывное начисление процентов

2.2.5. Определение срока ссуды и величины процентной ставки

2.3. Эквивалентность ставок и замена платежей

2.3.1. Эквивалентность процентных ставок

2.3.2. Изменение финансовых условий

test2. Тесты для проверки усвоения пройденного материала

Глава 3. Операции дисконтирования

3.1. Сущность дисконтирования

3.2. Математическое дисконтирование

3.3. Банковский учет

test3. Тесты для проверки усвоения пройденного материала

Глава 4. Потоки платежей и финансовые ренты

4.1. Сущность потока платежей и основные категории

4.2. Обобщающие характеристики финансовых потоков

4.2.1. Наращенная величина аннуитета

4.2.2. Современная (текущая) величина аннуитета

4.3. Определение параметром аннуитета

4.4. Оценка некоторых видов аннуитета

4.4.1. Бессрочный аннуитет

4.4.2. Непрерывный аннуитет

4.5. Нерегулярные потоки платежей

test4. Тесты для проверки усвоения пройденного материала

Глава 5. Инфляция в финансово-коммерческих расчетах

5.1. Сущность инфляции и необходимость ее учета в количественном анализе

5.2. Методы учета инфляции в финансовых расчетах

test5. Тесты для проверки усвоения пройденного материала

Часть 2. Типовые приложения финансовой математики

Глава 6. Финансовые функции ЕХСЕL как основа практических расчетов в современных условиях

6.1. Сущность финансовых функций

6.2. Использование финансовых функций в финансовых операциях

6.2.1. Операции наращения

6.2.2. Операции дисконтирования

6.2.3. Определение срока финансовой операции

6.2.4. Определение процентной ставки

Глава 7. Кредитные расчеты

7.1. Планирование погашения долга

7.1.1. Погашение долга единовременным платежом

7.1.2. Погашение долга в рассрочку

7.1.3. Потребительский кредит

Глава 8. Оценка инвестиционных процессов

8.1. Особенности инвестиционных процессов как объекта финансовой математики

8.2. Показатели эффекта и эффективности инвестиционных проектов

8.2.1. Чистый приведенный доход

8.2.2. Срок окупаемости

8.2.3. Внутренняя норма доходности

Приложение 1

Приложение 2

Приложение 3

Приложение 4

Приложение 5

Обозначения, используемые в данном пособии

Предисловие

Учебное пособие содержит систематизированное изложение основных понятий и методов финансовых вычислений и количественного анализа финансовых операций. Содержание курса охватывает базовые разделы финансовой математики, а также построение плана погашения кредита и финансовый анализ инвестиций. Базовые разделы финансовой математики и опирающиеся на них прикладные финансовые расчеты сопровождаются использованием технологии табличного процессора Excel.

Принятый в настоящем учебном пособии состав и последовательность рассмотрения учебного материала, позволяет получить целостное представление о финансово-экономических расчетах и о практическом применении этих методов при разработке и реализации финансовых решений.

Учебное пособие направлено на формирование профессионального уровня экономиста любой специальности. Кроме того, данный курс входит в подготовку бакалавров математиков, специализирующихся по направлению "прикладная математика" – математические методы и исследование операций в экономике. Возможно использование учебного курса для слушателей факультетов повышения квалификации экономических специальностей, а также для экономистов-практиков. Полученные студентами знания по финансовой математике являются основой для дальнейшего изучения ими дисциплин "Финансовый менеджмент", "Финансово-инвестиционный анализ", "Анализ рынка ценных бумаг", "Биржевое дело", "Страхование" и т.п.

Издание подготовлено на основе курсов лекций, читавшихся авторами на экономическом и математическом факультетах Алтайского государственного университета.

Учебный курс разработан при поддержке Национального фонда подготовки кадров в рамках Программы "Совершенствование социально-экономического образования в вузах".

Авторы благодарны экспертам НФПК за внимание и конструктивную критику.

Глава 2. Операции наращения

2.1. Простые проценты

2.1.1. Формула простых процентов

Рассмотрим процесс наращения (accumulation), т.е. определения денежной суммы в будущем, исходя из заданной суммы сейчас. Экономический смысл операции наращения состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Здесь идет движение денежного потока от на-стоящего к будущему.

Величина FV показывает будущую стоимость "сегодняшней" величины PV при заданном уровне интенсивности начисления процентов i.

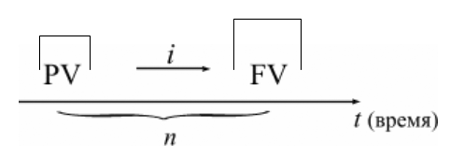Рис. 3. Логика финансовой операции наращения.

При использовании простых ставок процентов проценты (процентные деньги) определяются исходя из первоначальной суммы долга. Схема простых процентов предполагает неизменность базы, с которой происходит начисление процентов.

Из определения процентов не трудно заметить, что проценты (процентные деньги) представляют собой, по сути, абсолютные приросты:

I = FV - PV,

.

а поскольку база для их начисления является постоянной, то за ряд лет общий абсолютный прирост составит их сумму или произведение абсолютных приростов на количество лет ссуды:

I = (FV - PV)n = [(FV - PV)/PV • PV]n = i • PV • n,

где i = (FV - PV) / PV по определению процентной ставки.

Таким образом, размер ожидаемого дохода зависит от трех факторов: от величины инвестированной суммы, от уровня процентной ставки и от срока финансовой операции.

Тогда наращенную сумму по схеме простых процентов можно будет определять следующим образом:

FV = PV + I = PV + i • PV • n = PV (1 + i • n) = PV • k_н,

где k_н – коэффициент (множитель) наращения простых процентов.

Данная формула называется "формулой простых процентов".

Поскольку коэффициент наращения представляет собой значение функции от числа лет и уровня процентной ставки, то его значения легко табулируются. Таким образом, для облегчения финансовых расчетов можно использовать финансовые таблицы, содержащие коэффициенты наращения по простым процентам.

Пример 1. Сумма в размере 2'000 рублей дана в долг на 2 года по схеме простого процента под 10% годовых. Определить проценты и сумму, подлежащую возврату.

Решение:

Наращенная сумма:

FV = PV (1 + n • i ) = 2'000 (1 + 2 • 0'1) = 2'400 руб.

или

FV = PV • k_н = 2'000 • 1,2 = 2'400 руб.

Сумма начисленных процентов:

I = PV • n • i = 2'000 • 2 • 0,1 = 400 руб.

или

I = FV - PV = 2'400 - 2'000 = 400 руб.

Таким образом, через два года необходимо вернуть общую сумму в размере 2'400 рублей, из которой 2'000 рублей составляет долг, а 400 рублей – "цена долга".

Следует заметить, что подобные задачи на практике встречаются редко, поскольку к простым процентам прибегают в случаях:

• выдачи краткосрочных ссуд, т.е. ссуд, срок которых либо равен году, либо меньше его, с однократным начислением процентов;
• когда проценты не присоединяются к сумме долга, а периодически выплачиваются.

В тех случаях, когда срок ссуды менее года, происходит модификация формулы:

а) если срок ссуды выражен в месяцах (М), то величина n выражается в виде дроби:

n = М/12,

тогда все формулы можно представить в виде:

FV = PV (1 + М/12 • i);

I = PV • М/12 • i;

k_н = 1 + М/12 • i.

Пример 2. Изменим условия предыдущего примера, снизив срок долга до 6 месяцев.

Решение:

Наращенная сумма:

FV = PV (1 + М/12 • i) = 2'000 (1 + 6/12 • 0'1) = 2'100 руб.

или

FV = PV • k_н = 2'000 • 1,05 = 2'100 руб.

Сумма начисленных процентов:

I = PV • М/12 • i = 2'000 • 6/12 • 0,1 = 100 руб.

или

I = FV - PV = 2'100 - 2'000 = 100 руб.

Таким образом, через полгода необходимо вернуть общую сумму в размере 2'100 рублей, из которой 2'000 рублей составляет долг, а проценты – 100 рублей.

б) если время выражено в днях (t), то величина n выражается в виде следующей дроби:

n = t/T,

где t – число дней ссуды, т.е. продолжительность срока, на который выдана ссуда;

T – расчетное число дней в году (временная база).

Отсюда модифицированные формулы имеют следующий вид:

FV = PV (1 + t/T • i );

I = PV • t/T • i;

k_н = 1 + t/T • i.

Здесь возможны следующие варианты расчета:

1. Временную базу (T) можно представить по-разному:
• условно состоящую из 360 дней. В этом случае речь идет об обыкновенном (ordinary interest) или коммерческом проценте;
• взять действительное число дней в году (365 или 366 дней). В этом случае получают точный процент (exact interest).
2. Число дней ссуды (t) также можно по-разному определять:
• условно, исходя из того, что продолжительность любого целого месяца составляет 30 дней, а оставшиеся дни от месяца считают точно, – в результате получают так называемое приближенное число дней ссуды;
• используя прямой счет или специальные таблицы порядковых номеров дней года, рассчитывают фактическое число дней между датами, – в этом случае получают точное число дней ссуды. ^2>>>

Таким образом, если время финансовой операции выражено в днях, то расчет простых процентов может быть произведен одним из трех возможных способов:

1. Обыкновенные проценты с приближенным числом дней ссуды или, как часто называют, «германская практика расчета», когда продолжительность года условно принимается за 360 дней, а целого месяца – за 30 дней. Этот способ обычно используется в Германии, Дании, Швеции.
2. Обыкновенные проценты с точным числом дней ссуды, или "французская практика расчета", когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю. Этот способ имеет распространение во Франции, Бельгии, Испании, Швейцарии.
3. Точные проценты с точным числом дней ссуды, или "английская практика расчета", когда продолжительность года и продолжительность ссуды берутся точно по календарю. Этот способ применяется в Португалии, Англии, США.

Чисто формально возможен и четвертый вариант: точные проценты с приближенным числом дней ссуды, – но он лишен экономического смысла.

Вполне естественно, что в зависимости от использования конкретной практики начисления простых процентов их сумма будет различаться по абсолютной величине.

Для упрощения процедуры расчета точного числа дней финансовой операции пользуются специальными таблицами порядковых номеров дней года (Приложение 1), в которых все дни в году последовательно пронумерованы. Точное количество дней получается путем вычитания номера первого дня финансовой операции из номера последнего дня финансовой операции.

Пример 3. Сумма 2 млн руб. положена в банк 18 февраля не високосного года и востребована 25 декабря того же года. Ставка банка составляет 35% годовых. Определить сумму начисленных процентов при различной практике их начисления.

Решение:

1. Германская практика начисления простых процентов:

Временная база принимается за 360 дней, T = 360.

Количество дней ссуды: ^3>>>

t = 11 (февраль) + 30 (март) + 30 (апрель) + 30 (май) + 30 (июнь) + 30 (июль) + 30 (август) + 30 (сентябрь) + 30 (октябрь) + 30 (ноябрь) + 25 (декабрь) - 1 = 305 дней

Сумма начисленных процентов:

I = P • t/T • i = 2'000'000 • 305/360 • 0,35 = 593'055,55 руб.

1. Французская практика начисления процентов:

Временная база принимается за 360 дней, T = 360.

Количество дней ссуды:

t = 11 (февраль) + 31 (март) + 30 (апрель) + 31 (май) + 30 (июнь) + 31 (июль) + 31 (август) + 30 (сентябрь) + 31 (октябрь) + 30 (ноябрь) + 25 (декабрь) - 1 = 310 дней

По таблицам порядковых номеров дней в году (Приложение 1) можно определить точное число дней финансовой операции следующим образом:

t = 359 - 49 = 310 дней.

Сумма начисленных процентов:

I = P • t/T • i = 2'000'000 • 310/360 • 0,35 = 602'777,78 руб.

1. Английская практика начисления процентов:

Временная база принимается за 365 дней, T = 365.

Количество дней ссуды берется точным, t = 310 дней.

Сумма начисленных процентов:

I = P • t/T • i = 2'000'000 • 310/365 • 0,35 = 594'520,55 руб.

Как видно, результат финансовой операции во многом зависит от выбора способа начисления простых процентов. Поскольку точное число дней в большинстве случаев больше приближенного числа дней, то и проценты с точным числом дней ссуды обычно получаются выше процентов с приближенным числом дней ссуды.

В практическом смысле эффект от выбора того или иного способа зависит от значительности сумм, фигурирующих в финансовой операции.

<<<2	Внимание: при определении продолжительности финансовой операции дата выдачи и дата погашения считаются за один день.
<<<3	Не забудьте: день выдачи и день возвращения ссуды считаются за один день.

Переменные ставки

Ставка процентов не является застывшей на вечные времена величиной, поэтому в финансовых операциях, в силу тех или иных причин, предусматриваются дискретно изменяющиеся во времени процентные ставки. Например, наличие инфляции вынуждает собственника денег периодически варьировать процентной ставкой. В таких случаях наращенную сумму определяют, используя следующую формулу:

FV = PV • (1 + n₁ • i₁ + n₂ • i₂ + … + n_k • i_k),

где k – количество периодов начисления;

n_k – продолжительность k-го периода;

i_k – ставка процентов в k-ом периоде.

Пример 5. Вклад в сумме 5'000 руб. был положен в банк 25 мая не високосного года по ставке 35% годовых, а с 1 июля банк снизил ставку по вкладам до 30% годовых и 15 июля вклад был востребован. Определить сумму начисленных процентов при английской практике их начисления.

Решение:

Количество дней для начисления процентов по первоначально действующей процентной ставке в размере 35% годовых рассчитывается точно и составляет 37 дней, а по измененной ставке 30% годовых – 14 дней.

Отсюда величина процентов будет равна:

I = 5'000 • (37/365 • 0,35 + 14/365 • 0,30) = 234,93 руб.

Таким образом, при закрытии счета клиент должен получить процентов в сумме 234,93 руб.

Сложные проценты

2.2.1. Формула сложных процентов

В финансовой практике значительная часть расчетов ведется с использованием схемы сложных процентов.

Применение схемы сложных процентов целесообразно в тех случаях, когда:

• проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов;
• срок ссуды более года.

Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга:

FV = PV + I = PV + PV • i = PV • (1 + i)

– за один период начисления;

FV = (PV + I) • (1 + i) = PV • (1 + i) • (1 + i) = PV • (1 + i)²

– за два периода начисления;

отсюда, за n периодов начисления формула примет вид:

FV = PV • (1 + i) n = PV • k_н ,

где FV – наращенная сумма долга;

PV – первоначальная сумма долга;

i – ставка процентов в периоде начисления;

n – количество периодов начисления;

k_н – коэффициент (множитель) наращения сложных процентов.

Эта формула называется формулой сложных процентов.

Как было выше указано, различие начисления простых и сложных процентов в базе их начисления. Если простые проценты начисляются все время на одну и ту же первоначальную сумму долга, т.е. база начисления является постоянной величиной, то сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу. Таким образом, простые проценты по своей сути являются абсолютными приростами, а формула простых процентов аналогична формуле определения уровня развития изучае-мого явления с постоянными абсолютными приростами. Сложные проценты характери-зуют процесс роста первоначальной суммы со стабильными темпами роста, при нара-щении ее по абсолютной величине с ускорением, следовательно, формулу сложных процентов можно рассматривать как определение уровня на базе стабильных темпов роста.

Согласно общей теории статистики, для получения базисного темпа роста необходимо перемножить цепные темпы роста. Поскольку ставка процента за период является цепным темпом прироста, то цепной темп роста равен:

(1 + i)

Тогда базисный темп роста за весь период, исходя из постоянного темпа прироста, имеет вид:

(1 + i)ⁿ

Базисные темпы роста или коэффициенты (множители) наращения, зависящие от процентной ставки и числа периодов наращения, табулированы и представлены в Приложении 2. Экономический смысл множителя наращения состоит в том, что он показывает, чему будет равна одна денежная единица (один рубль, один доллар и т.п.) через n периодов при заданной процентной ставке i. ^5>>>

Графическая иллюстрация соотношения наращенной суммы по простым и сложным процентам представлена на рисунке 4.

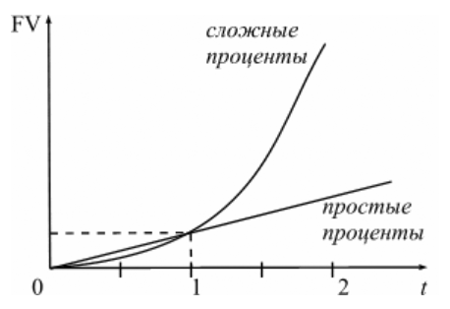Рис. 4. Наращение по простым и сложным процентам.

Как видно из рисунка 4, при краткосрочных ссудах начисление по простым процентам предпочтительнее, чем по сложным процентам; при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам значительно выше, чем по простым.

При любом i,

если 0 < n < 1, то (1 + ni) > (1 + i)ⁿ

если n > 1, то (1 + ni) < (1 + i)ⁿ

если n = 1, то (1 + ni) = (1 + i)ⁿ

Таким образом, для лиц, предоставляющих кредит:

• более выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года);
• более выгодной является схема сложных процентов, если срок ссуды превышает один год;
• обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.

Пример 8. Сумма в размере 2'000 долларов дана в долг на 2 года по ставке процента равной 10% годовых. Определить проценты и сумму, подлежащую возврату.

Решение:

Наращенная сумма

FV = PV• (1 + i)_n = 2'000 • (1 + 0'1)₂ = 2'420 долларов

или

FV = PV • k_н = 2'000 • 1,21 = 2'420 долларов,

где k_н = 1,21 (Приложение 2).

Сумма начисленных процентов

I = FV - PV = 2'420 - 2'000 = 420 долларов ^6>>>

Таким образом, через два года необходимо вернуть общую сумму в размере 2'420 долларов, из которой 2'000 долларов составляет долг, а 420 долларов – "цена долга".

Достаточно часто финансовые контракты заключаются на период, отличающийся от целого числа лет.

В случае, когда срок финансовой операции выражен дробным числом лет, начисление процентов возможно с использованием двух методов:

• общий метод заключается в прямом расчете по формуле сложных процентов:

FV = PV • (1 + i)ⁿ,

n = a + b,

где n – период сделки;

a – целое число лет;

b – дробная часть года.

• смешанный метод расчета предполагает для целого числа лет периода начисления процентов использовать формулу сложных процентов, а для дробной части года – формулу простых процентов:

FV = PV • (1 + i)^a • (1 + bi)

Поскольку b < 1, то (1 + bi) > (1 + i)^a, следовательно, наращенная сумма будет больше при использовании смешанной схемы.

Пример. В банке получен кредит под 9,5% годовых в размере 250 тыс. дол-ларов со сроком погашения через два года и 9 месяцев. Определить сумму, которую необходимо вернуть по истечении срока займа двумя способами, учитывая, что банк использует германскую практику начисления процентов.

Решение:

Общий метод:

FV = PV • (1 + i)ⁿ = 250 • (1 + 0,095)^2,9 =

= 320,87 тыс. долларов.

Смешанный метод:

FV = PV • (1 + i)^a • (1 + bi) =

= 250 • (1 + 0,095)² • (1 + 270/360 • 0,095) =

= 321,11 тыс. долларов.

Таким образом, по общему методу проценты по кредиту составят

I = S - P = 320,87 - 250,00 = 70,84 тыс. долларов, ^7>>>

а по смешанному методу

I = S - P = 321,11 - 250,00 = 71,11 тыс. долларов.

Как видно, смешанная схема более выгодна кредитору.

<<<5	При пользовании финансовыми таблицами необходимо сле-дить за соответствием длины периода и процентной ставки.
<<<6	Сравните полученный результат с результатом примера 1. Не трудно заметить, что сложная ставка дает большую сумму процентов.
<<<7	При расчете по смешанному методу результат всегда оказывается больше.

Переменная ставка процентов

Необходимо отметить, что основная формула сложных процентов предполагает постоянную процентную ставку на протяжении всего срока начисления процентов. Однако, предоставляя долгосрочную ссуду, часто используют изменяющиеся во времени, но заранее зафиксированные для каждого периода ставки сложных процентов. В случае использования переменных процентных ставок, формула наращения имеет следующий вид:

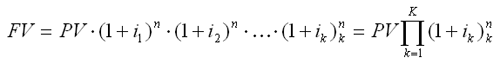где i_k – последовательные во времени значения процентных ставок;

n_k – длительность периодов, в течение которых используются соответствующие ставки.

Пример. Фирма получила кредит в банке на сумму 100'000 долларов сроком на 5 лет. Процентная ставка по кредиту определена в 10% для 1-го года, для 2-го года предусмотрена надбавка к процентной ставке в размере 1,5%, для последующих лет 1%. Определить сумму долга, подлежащую погашению в конце срока займа.

Решение:

Используем формулу переменных процентных ставок:

FV = PV • (1 + i₁)ⁿ₁ • (1 + i₂)ⁿ₂ • … • (1 + i_k)ⁿ_k =

100'000 • (1 + 0,1) • (1 + 0,115) • (1 + 0,125)³ =

174'632,51 долларов

Таким образом, сумма, подлежащая погашению в конце срока займа, составит 174'632,51 доллара, из которых 100'000 долларов являются непосредственно суммой долга, а 74'632,51 доллара – проценты по долгу.

Банковский учет

Банковский учет – второй вид дисконтирования, при котором исходя из известной суммы в будущем, определяют сумму в данный момент времени, удерживая дисконт.

Операция учета (учет векселей) заключается в том, что банк или другое финансовое учреждение до наступления платежа по векселю покупает его у предъявителя по цене ниже суммы векселя, т.е. приобретает его с дисконтом. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя. При этом банк удерживает в свою пользу проценты (дисконт) от суммы векселя за время, оставшееся до срока его погашения. Подобным образом (с дисконтом) государство продает большинство своих ценных бумаг.

Для расчета дисконта используется учетная ставка:

• >простая учетная ставка:

D = FV - PV = FV • n • d = FV • t/T • d ,

где n – продолжительность срока в годах от момента учета до даты выплаты известной суммы в будущем.

Отсюда:

PV = FV - FV • n • d = FV • (1 - n • d),

где (1 - n • d) – дисконтный множитель.

Очевидно, что чем выше значение учетной ставки, тем больше дисконт. Дисконтирование по простой учетной ставке чаще всего производится по французской практике начисления процентов, т.е. когда временная база принимается за 360 дней, а число дней в периоде берется точным.

Пример. Вексель выдан на 5'000 руб. с уплатой 17 ноября, а владелец учел его в банке 19 августа по учетной ставке 8%. Определить сумму, полученную предъявителем векселя и доход банка при реализации дисконта.

Решение:

Для определения суммы при учете векселя рассчитываем число дней, оставшихся до погашения обязательств:

t = 13 (август) + 30 (сентябрь) + 31 (октябрь) + 17 (ноябрь) - 1 = 90 дней.

Отсюда, определяемая сумма:

PV = FV • (1 - t/T • d) =

5'000 • (1 - 90/360 • 0,08) = 4'900 руб.

Тогда дисконт составит:

D = FV - PV = 5'000 - 4'900 = 100 руб.

или

D = FV • t / T • d = 5'000 • 90/360 • 0,08 = 100 руб.

Следовательно, предъявитель векселя получит сумму 4'900 руб., а банк при наступлении срока векселя реализует дисконт в размере 100 руб.

• по сложной учетной ставке:

PV = FV •╥(1 - d)ⁿ

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, т.к. учетная ставка каждый раз применяется к уменьшаемой на величину дисконта величине.

Пример. Определить величину суммы, выдаваемую заемщику, если он обязуется вернуть ее через два года в размере 55 тыс. руб. Банк определяет свой доход с использованием годовой учетной ставки 30%.

Решение:

Используя формулу дисконтирования по сложной учетной ставке, определяем:

PV = FV • (1 - d)ⁿ = 55'000 • (1 - 0,3)² = 26'950 руб.

Заемщик может получить ссуду в размере 26'950 руб., а через два года вернет 55 тыс. руб.

Объединение платежей можно производить и на основе учетной ставки, например, при консолидировании векселей. В этом случае, сумма консолидированного платежа рассчитывается по следующей формуле:

FV_oб = ΣFV_j•(1 - d • t_j)^-1,

где t_j – интервал времени между сроками векселей.

Пример. Вексель на сумму 10 тыс. руб. со сроком погашения 10.06, а также вексель на сумму 20 тыс. руб. со сроком погашения 01.08 заменяются одним с продлением срока до 01.10. При объединении векселей применяется учетная ставка 25%. Определить сумму консолидированного векселя.

Решение:

Для использования формулы консолидированного платежа необходимо определить срок пролонгации векселей:

t₁ = 21 (июнь) + 31 (июль) + 31 (август) + 30 (сентябрь) + 1 (октябрь) - 1 = 113 дней,

t₂ = 31 (август) + 30 (сентябрь) + 1(октябрь) - 1 = 61 день.

Тогда, сумма консолидированного векселя:

FV_o = ΣFV_j • (1 - d • t_j)^-1 =

10'000 • (1 - 113/360 • 0,25)^-1 + 20'000 • (1 - 61/360 • 0,25)^-1 =

=31'736 руб.

Таким образом, сумма консолидированного векселя с датой погашения 01.10 составит 31'736 руб.

В том случае, когда учету подлежит долговое обязательство, по которому предусматривается начисление процентов, происходит совмещение начисления процентов по процентной ставке и дисконтирования по учетной ставке:

PV₂ = PV₁ • (1 + n₁ • i ) • (1 - n₂ • d ),

где PV₁ – первоначальная сумма долга;

PV₂ – сумма, получаемая при учете обязательства;

n₁ – общий срок платежного обязательства;

n₂ – срок от момента учета до погашения.

Пример. Обязательство уплатить через 100 дней сумму долга в размере 50 тыс. руб. с начисляемыми на нее точными процентами по ставке 40%, было учтено за 25 дней до срока погашения по учетной ставке 25%. Определить сумму, полученную при учете обязательства.

Решение:

Следует обратить внимание на различие временных баз, используемых при наращении и учете:

PV₂ = PV₁ • (1 + n_1/ • i ) • (1 - n₂ • d) =

50'000 • (1 + 100/365 • 0,4) • (1 - 25/360 • 0,25) = 54'516 руб.

Следовательно, сумма, получаемая при учете данного обязательства, составит 54'516 руб.

Непрерывный аннуитет

Если промежутки между последовательными поступлениями являются бесконечно малой величиной, то такой аннуитет считают непрерывным, т.е. денежные поступления происходят непрерывно с постоянной интенсивностью.

При начислении непрерывных процентов для получения формул определения наращенной или современной величины потока платежей необходимо перейти к пределу, откуда:

• наращенная величина потока платежей

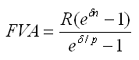· где σ – сила роста.

• современная величина потока платежей

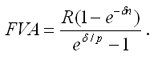Операции дисконтирования

Для многих финансовых операций необходимо использовать данные о приведенных или современных денежных величинах, как разовой суммы, так и потоков фиксированных периодических платежей. Для облегчения расчетов используется функция ПЗ – первоначальное значение (PV).

Аргументы функции:

• норма;
• кпер;
• выплата;
• БС;
• тип.

Этот расчет является обратным к определению наращенной суммы при помощи функции БЗ, поэтому сущность используемых аргументов в этих функциях аналогична. Вместе с тем, вводится новый аргумент БС – будущая стоимость или будущее значение денежной суммы (FV), а также иное обозначение числа периодов – кпер – (n или n • m).

Рассматриваемая функция может быть использована для расчета по простым и сложным процентам.

Пример. Через 125 дней следует накопить сумму в размере 2,5 тыс. руб. Какой должен быть размер вклада, размещаемый под 5%?

Решение:

Определяем первоначальную сумму долга:

норма	125/360 • 5%
кпер
выплата
БС	2500*
тип

*Положительное значение означает поступление денег.

Значение -2457,34 ^10>>>

На указанных условиях следует положить 2'457,34 руб., что позволит через 125 дней получить 2'500 ,00 руб.

Текущее значение единой суммы вклада с использованием сложных процентов и неоднократным начислением процентов в течение года рассчитывается аналогично.

Пример. Требуется получить на лицевом счете 50 тыс. руб. через три года. Выбрать варианты размещения средств:

• под 26% с полугодовым начислением процентов;
• под 24% годовых с ежеквартальным начислением процентов.

Решение:

Используем функцию ПЗ.

Для первого варианта:

норма	26% / 2
кпер	3 • 2
выплата
БС
тип

Значение -24015,93.

Для второго варианта:

норма	24% / 4
кпер	3 • 4
выплата
БС
тип

Значение -24848,47.

Таким образом, предпочтителен первый вариант, поскольку имеет меньшую первоначальную величину.

При определении современной величины аннуитета следует помнить, что чем дальше отстоит от настоящего момента член ренты, тем меньшую текущую стоимость он представляет.

Пример. Какую сумму необходимо положить в банк, чтобы в течение 8 лет в начале каждого года снимать по 24 тыс. руб., если процентная ставка составляет 6% годовых?

Решение:

норма	6%
кпер
выплата
БС
тип

Значение -157977,15

Таким образом, чтобы иметь возможность ежегодно в начале года в течение 8 лет снимать по 24'000,00 руб., необходимо положить 157'977,15 руб.

Если функция ПЗ используется при расчете аннуитетов, то функция НПЗ используется для переменной ренты, т.е. для ренты с неравными членами.

<<<10

Знак минус означает отток денег.

Глава 7. Кредитные расчеты

7.1. Планирование погашения долга

7.1.1. Погашение долга единовременным платежом

Количественный анализ долгосрочной задолженности (займа) применяется для достижения сбалансированности, т.е. адекватности его параметров принятым условиям финансового соглашения, путем планирования погашения долга.

Планирование погашения долга заключается в определении периодических расходов, связанных с займом, – такие расходы называются обслуживанием долга. Разовая сумма обслуживания долга – срочная уплата, в которую входят:

• текущие процентные платежи;
• средства, для погашения (амортизации) основной суммы долга.

Размеры срочных уплат зависят от условий займа:

• срока;
• наличия и продолжительности льготного периода;
• уровня процентной ставки;
• способа погашения основной суммы долга и выплаты процентов.

Для кредитной схемы в качестве исходных параметров выступают величина займа (D), срок его погашения (n), процент по кредиту (i), под который выдаются деньги, и поток платежей по выплате долга (Y_t).

Рассмотрим различные способы погашения задолженности, поскольку от выбора способа погашения стоимость кредита (сумма выплачиваемых процентов) будет различной. Здесь возможны два варианта:

а) погашение единовременным платежом, т.е. возврат всей суммы в оговоренный срок;

б) погашение долга в рассро