Как видно, результат финансовой операции во многом зависит от выбора способа начисления простых процентов.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по дисциплине “Финансовая математика” для студентов специальности 7.050104 “Финансы” всех форм обучения
Севастополь
УДК 658.14
Методические указания к практическим занятиям по дисциплине «Финансовая математика» для студентов специальности 7.050104 «Финансы» всех форм обучения / Сост. Н.А. Глухова, В.В. Ольховик. – Севастополь: Изд-во СевНТУ, 2008 – 61 с.
 Целью методических указаний является обеспечение студентов учебно – методическими материалами, необходимыми для формирования знаний, навыков проведения коммерческих и финансовых, умений интерпретировать полученные результаты.
Целью методических указаний является обеспечение студентов учебно – методическими материалами, необходимыми для формирования знаний, навыков проведения коммерческих и финансовых, умений интерпретировать полученные результаты.
Методические указания предназначены для студентов специальности 7.050104 “Финансы” всех форм обучения.
Методические указания рассмотрены и утверждены на заседании кафедры “Финансы и кредит” (протокол № 5 от 28.12.2007 г.)
Допущено учебно – методическим центром СевНТУ в качестве методических указаний.
Рецензенты:
Гридина Н.М. к.э.н., доц.
СОДЕРЖАНИЕ
Введение……………………………………………………………………………………………..4
Тема 1. Предмет и категории финансовой математики …………………………………………4
Практическое занятие 1. Предмет и категории финансовой математики …...............…4
Тема 2. Расчеты по простым процентам ……………………………….………………................ 5
Практическое занятие 2. Декурсивный метод начисления простых процентов.........… 5
Практическое занятие 3. Антисипативный метод начисления простых процентов …11
Тема 3. Расчеты по сложным процентам …………………………………………………….......14
Практическое занятие 4 Декурсивный метод начисления сложных процентов……....14
Практическое занятие 5 Антисипативный метод начисления сложных процентов…..18
Тема 4. Эквивалентность процентных ставок и платежей…………………………………….…23
Практическое занятие 6. Эквивалентность процентных ставок и платежей….….….....23
Тема 5. Финансовые ренты ………………………………………………………………………..27
Практическое занятие 7. Наращение аннуитетов (финансовой ренты)………..…..…....27
Практическое занятие 8. Современная стоимость финансовых рент……………..…….31
Практическое занятие 9. Конверсия финансовых рент и анализ переменных денежных потоков………………………………………………….…………………………………….….35
Тема 6. Планирование погашения задолженности, конверсия займов, ипотечные ссуды ……..37
Практическое занятие 10. Конверсия займов и формирование фонда погашения……....37
Практическое занятие 11. Погашение ипотечной ссуды…………………………….…….42
Библиографический список……...…………………………………………………………..…… ..47
ПРИЛОЖЕНИЕ А (справочное) - порядковые номера дней года………………………..……..48
ПРИЛОЖЕНИЕ Б (справочное) – коэффициенты приведения 1 ден. ед. PVIF n,i ……….....….49
ПРИЛОЖЕНИЕ В (справочное) – коэффициенты наращения 1 ден. ед. FVIF n,i…………......50
ПРИЛОЖЕНИЕ Г (справочное) – коэффициенты приведения 1 ден. ед. финансовой ренты PVIFA n,i………………………………………………………………………………….….…….....51
ПРИЛОЖЕНИЕ Д (справочное) – коэффициенты наращения 1 ден. ед. финансовой ренты FVIFA n,i…………………………………………………………………………………….……… 52
ПРИЛОЖЕНИЕ Е(справочное) – коэффициенты наращения 1 ден. ед. p-срочной ренты PFVIFA n,i……………………………………………………………………………………………………....53
ВВЕДЕНИЕ
Методические указания и задания подготовлены в соответствии с программой нормативной дисциплины «Финансовая математика», которая включена в обязательный перечень курсов бакалаврского уровня подготовки студентов экономических специальностей. Настоящие методические указания и задания разработаны с целью изучения студентами на практических занятиях методов финансовых расчетов.
В результате выполнения практических заданий студенты должны:
- знать основные методы проведения финансовых расчетов на уровне предприятий, банковских учреждений, страховых организаций;
- уметь рассчитывать параметры финансовых операций;
- проводить сравнительный анализ вариантов осуществления финансовых сделок.
Издание включает теоретические аспекты, планы практических занятий, задания и вопросы для самостоятельного контроля качества знаний теоретических положений курса.
ТЕМА 1. ПРЕДМЕТ И КАТЕГОРИИ ФИНАНСОВОЙ МАТЕМИТИКИ
Практическое занятие 1. Предмет и категории финансовой математики
Цель: Закрепить знания ключевых категорий темы.
Проведение любой финансовой, коммерческой операции предполагает наличие условий ее осуществления. Данный факт требует проведения количественного финансового анализа осуществляемых операций.
Предметом финансовой математики является совокупность методов расчетов.
В финансовой математике выделяют две основные категории: проценты и процентные ставки.
Проценты в финансовых расчетах – это абсолютная сумма дохода от предоставления капитала в долг или от инвестиций производственно-финансового характера. Понятие процента связано с такой категорией как время. Концепция времени определяет капитал, вложенный в дело, приносящий процент, т.о. фактор времени определяет принцип не равноценности денежных сумм, относящихся к разным моментам времени.
Процентная ставка – это величина, характеризующая интенсивность начисления процентов и определяемая как отношение суммы процентных денег, полученных за определенный период к величине кредита или сумме инвестиций.
В финансовых расчетах процентные ставки используются в виде коэффициента. Этот показатель рассчитывается как отношение приращения исходной суммы к базовой величине, в качестве которой, очевидно, можно взять либо РV, либо FV(настоящая и будущая стоимость).
Вопросы для обсуждения:
- финансовая математика как наука и учебная дисциплина
- причины, сдерживающие развитие финансовой математики в отечественной практике финансовых расчетов
- роль фактора времени в финансовых операциях
- взаимосвязь финансовой математики с другими дисциплинами (привести примеры)
- определение процентов в математике и в финансовых расчетах
- процентные ставки, их функции и классификация
- арифметическая, геометрическая прогрессия
- виды процентных ставок;
Задачи
1. Выразить следующие проценты в виде соответствующих натуральных и десятичных дробей с точностью до четвертого десятичного знака:
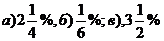
г)4%, д)3,2%. е) 0,8%.
2. Представить каждую из следующих дробей в виде процентов с точностью до сотой доли процентов:
а)0,035; б)0,04, в)3/40; г)5/16; д)8,40/280
3. Иванов взял в сберегательном банке ссуду 10 000 грн. Если банк начисляет 250 грн. процентов за использование этой суммы в течение шести месяцев, какой будет ставка процентов за этот период?
4. Иванов взял в долг у Петрова некоторую сумму денег без процентов и обещал вернуть в течении 11 дней следующим образом: в 1 день 110 д.е., а в последующие дни уменьшая сумму каждого предыдущего дня на 10 д.е..
Определить:
- Чему равна сумма, выплаченная Ивановым в последний день
- Какую сумму Иванов занял у Петрова
5. За сколько месяцев будет возвращена сумма, взятая без процентов, если стороны договорились, что в первый месяц должник выплатит 10 д.е., а в каждый последующий месяц сумма будет возрастать на 5 д.е. по сравнению с предыдущим, и в последний месяц составит 80 д.е. На какую сумму заключен договор?
6. В течение 10 месяцев на предприятие будут поступать платежи, уменьшающиеся каждый месяц в 0,5. Если последний платеж составит 7 д.е. определить
- размер первого платежа и общую сумму платежей,
- размер пятого платежа
7. Определить первую и последнюю выплату из 8 существующих, если общая сумма выплат составляет 765 д.е., а каждая выплата по отношению к предыдущей увеличивается в 2 раза.
8. Банк «Кредит» на вклад, внесенный 23.07 текущего года, начислял следующие годовые проценты: 23.07 – 19%, с 24.07 по 31.07 – 18.5%, с 1.08 по 25.08 – 17%, с 26.08 по 6.09 – 16.5%, с 7.09 по 13.09 –16%, с 14.09 по 24.09 – 15%. Определить среднюю процентную ставку за данный период.
9. Месячные уровни инфляции с февраля по июль текущего года следующие: февраль – 4%, март – 5%, апрель – 4.5%, май –3%, июнь – 3.5%, июль –3%. Определить среднее значение инфляции за указанный период .
10. Клиент разместил три срочных депозита в банки на срок 3, 6 и 2 месяца. Процентные ставки соответственно – 14%, 18%, 11%. Определить средневзвешенную процентную ставку.
2. РАСЧЕТЫ ПО ПРОСТЫМ ПРОЦЕНТАМ
Практическое занятие 2, Декурсивный метод начисления простых процентов
Цель: Изучить теоретические основы и получить практические навыки при расчетах по простым процентам декурсивным методом.
Наращение - процесс определения будущей стоимости по известной нынешней, от есть процесс начисления процентов на основную сумму.
Наращение по простым процентам используется для выдачи краткосрочных ссуд с однократным начислением процентов.
Наращением или ростом называется процесс увеличения некоторой суммы денег за счет начисления на нее процентов.
Дисконтирование - процесс определения нынешней стоимости по известной будущей (процесс приведения, процесс обратный наращению).
Простые проценты начисляются на одну и ту же первоначальную сумму (то есть добавления начисленных за первый период процентов к первоначальной сумме не производится).
Введем обозначения:
PV (Present value), P - нынешняя, первоначальная сумма;
FV (future value), S - будущая, наращенная сумма;
i - ставка процента;
n - количество лет;
m - количество периодов начисления процентов в году (например, m=4 если проценты начисляются ежеквартально).
Проценты (процентные деньги) представляют собой абсолютные приросты:
I=FV-PV,
а поскольку база для их начисления является постоянной, то за ряд лет общий абсолютный прирост составит их сумму или произведение абсолютных приростов на количество лет ссуды:
I = (FV-PV)*n= 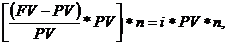
где 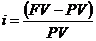 по определению процентной ставки.
по определению процентной ставки.
Следовательно, наращенная сумма вычисляется по формуле
FV = PV + I, (2.1)
Сумма начисленных процентов вычисляется по формуле
I= PV * i* n, (2.2)
Формула наращения простыми процентами:
FV = PV + PV*i*n = PV*(1+i*n). (2.3)
При изменении процентной ставки из периода в период наращенная сумма определяется по формуле
FV=PV*(1+n1i1+n2i2+….+nkik), (2.4)
где n1,n2,….nk – расчетные периоды, в которых начисление процентов производится соответственно по ставкам i1, i2,...,ik
| Наращение | Дисконтирование |
| FV = PV*(1 + i*n) | PV = FV / (1+ i*n) (2.5) |
| Если проценты по 2-летнему вкладу начисляются m раз в году (промежуточные проценты), необходимо процентную ставку разделить на m (то есть при ежеквартальном начислении по ставке 24% годовых каждый квартал будет начисляться 6 % (24% / 4) первоначальной суммы, а начислять проценты будут 8 (2*4) раз). | |
FV = PV*(1 + 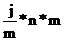 ) ) | PV = FV / (1 + 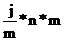 ) (2.6) ) (2.6) |
Как видно из приведенных формул, количество периодов начисления m не влияет на результат наращения и дисконтирования по простым процентам.
Если срок операции не целое число лет, n=t/k; где
t - срок операции в единицах соответствующей временной базы k
k= 12, 4, 360/365, 366
Для упрощения процедуры расчета точного числа дней пользуются специальными таблицами, в которых все дни в году последовательно пронумерованы. Продолжительность финансовой операции определяется вычитанием номера первого дня из номера последнего дня. (см. Приложение А).
В зависимости от выбранной методики при расчете сроков финансовой операции могут использоваться методики, приведенные в таблице 2.1.
Таблица 2.1.- Методики расчета срока финансовой операции
| Вариант начисления процентов | Порядок расчетов сроков операции | Временная база | Примечание |
| Точные проценты с точным числом дней | Фактическое число дней определяемое по календарю или специальной таблице | 365, 366 | Английская практика |
| Обыкновенные проценты с точным числом дней в течении операции | Фактическое число дней определяемое по календарю или специальной таблице | Французская практика | |
| Обыкновенные проценты с приближенным числом дней в течении финансовой операции | Расчет числа дней операции осуществляют исходя из того, что в каждом месяце 30 дн. | Немецкая практика |
При проведении финансовой операции день выдачи и погашения ссуды считается за 1 день.
Вопросы для обсуждения:
- сущность процентных платежей;
- наращенная сумма по простым процентам;
- исчисление обычных, коммерческих, точных процентов;
- применение простых процентов в потребительском кредите;
- изменяющаяся простая ставка процентов;
- учет инфляции в финансовых операциях;
- стоимость денег и время;
- сущность дисконтирования;
- виды дисконтирования.
Примеры решения задач
Пример 2.1. Фирме выделен банковский кредит на срок с 3 января по 12 марта под простые проценты с процентной ставкой 12% годовых. Сумма кредита - 80 тыс. грн. Определить по трем методам коэффициент наращения и наращенную сумму.
Решение:
Коэффициент наращения рассчитывается по формуле:
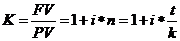
Расчет коэффициентов наращения по трем методам наращения:
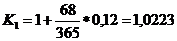
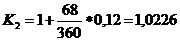
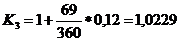
Расчет наращенных сумм:
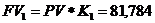
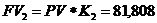
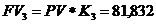
Ответ: K1=1,0223; K2 = 1,0226; K3=1,0229. Очевидно, что фирме предпочтительнее расчет коэффициента наращения по первому методу. Особенно заметны финансовые различия при k > 360 .
Пример 2.2. Фирма взяла в коммерческом банке кредит на сумму 600 тыс. грн.
сроком на 4 года. Согласно договору, за первый год процентная ставка составляла 14% и с учетом инфляции каждый последующий год повышалась на 2 пункта. Определите коэффициент наращения, наращенную сумму и доход банка.
Решение:
Расчет коэффициента наращения в случае использования изменяющейся процентной ставки:
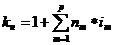
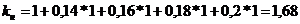
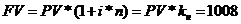 (тыс.грн)
(тыс.грн)
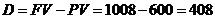 (тыс.грн.)
(тыс.грн.)
Ответ: kн=1,68; FV=1008 (тыс.грн.); D=408 (тыс.грн.)
Пример 2.3 Сумма в размере 2000 грн. положена в банк 18 февраля не высокосного года и востребована 25 декабря того же года. Ставка банка составляет 15 процентов. Определить сумму начисленных процентов при французской и английской практике их начисления.
Решение:
Французская практика расчётов:
По таблицам порядковых номеров дней в году (Приложение А) можно определить точное число дней финансовой операции следующим образом:
T=359-49 = 310 дней,
Сумма начисленных процентов:
I= PV*t/k*i=2000*310/360*0,15=258,33 (грн.)
Английская практика расчётов:
I=2000*310/365*0,15=254,8 (грн)
Задачи
1. Предприятие взяло кредит 100000 грн. сроком на 2 года под 15% годовых и по истечении заемного периода должно вернуть кредит с процентами. Сколько должно заплатить предприятие? Проценты простые.
2. Молодая семья получила в банке ссуду на строительство жилья в размере 60 тыс. грн. сроком на 3 года под простую процентную ставку 21% годовых. Определите наращенную сумму кредита и сумму процентов.
3. Банк принимает вклады на срочный депозит на следующих условиях: процентная ставка при сроке 180 дней – 14%; при сроке 240 дней – 15; при сроке 270 дней –16%. Рассчитайте доход клиента при вкладе 10 тыс. грн. на указанные сроки. Год не високосный. Методика расчета: точные проценты с точным числом дней.
4. Клиент вложил в банк на депозит 2000$ на срок с 12 апреля по 26 июня с простой процентной ставкой 4% годовых. Рассчитайте доход клиента по трем методикам. Год не високосный.
5. Фирма внесла в коммерческий банк 28 тыс. грн. на срок с 9 ноября по 21 ноября того же года. На вклады «до востребования» банк начисляет проценты – 9% годовых. Проценты обыкновенные с приближенным числом дней в году. Определите наращенную сумму.
6. Коммерческий банк привлекает средства населения под простые проценты с процентной ставкой 17% годовых. Клиент внес 6 тыс. грн. на депозит с 12 февраля по 24 апреля. Определите величину коэффициента наращения и наращенную сумму для случая: а) точных процентов с точным числом дней; в) обыкновенных процентов с приближенным числом дней. Год не високосный.
7. Правекс – банк предлагает следующие условия для вкладов физических лиц: выплата процентов – ежемесячно, без права пополнения вклада, сумма вклада от 250 грн. проценты простые, методика расчеты точные проценты с точным числом дней. Необходимо рассчитать ежемесячную наращенную сумму и доход студента от полученной стипендии в размере 300 грн на срок 2 года.
| Название вклада | Сумма вклада | 1 мес | 2 мес. | 3 мес. | 6 мес. | 9 мес | 12 мес. и 3 дн. | 15 мес. | 18 мес. | 24 мес. |
| Правекс стандарт плюс | От 250 грн. | - | 7,8 | 11,6 | 12,6 | 13,6 | 14,5 | 14,8 | 15,3 |
8. Клиент внес в банк 14 тыс. грн. на срок с 14 февраля по 23 июля. На вклады «до востребования» сроком больше месяца банк начисляет 7% годовых. Определите наращенную сумму при расчете по: а) точным процентам с точным числом дней; б) банковскому методу; в) обыкновенным процентам с приближенным числом дней. Год не високосный.
9. Коммерческий банк выдал ссуду в сумме 75 000 грн. под 15,5% простых годовых. По истечении срока кредита заемщик должен вернуть 85 000 грн. Определить срок, на который выдан кредит.
10. Банком был привлечен депозит 01.03.01 в сумме 3 500 грн. под 18% простых годовых. В конце срока депозита банк обязан выплатить клиенту 3850 грн. Определить срок депозита и дату его возврата.
11. На какой срок выдан кредит в 300 тыс. грн. под процентную ставку 25% годовых, если банк получил сумму от кредитора 380 тыс. грн. Методика расчета: обыкновенных % с приближенным числом дней.
12. Определите, какую процентную ставку должна установить при кредите 2000$ финансовая компания, чтобы при сроке кредита в 184 дня иметь прибыль не менее 120$. Проценты обыкновенные с приближенным числом дней.
13. Клиент получил кредит сроком на 9 месяцев в 6 тыс. грн. Сумма возврата кредита – 6,3 тыс. грн. Определите процентную ставку банка.
14. Коммерческий банк выдал кредит на период с 1.03 по 1.06 в сумме 150 000 грн. под 24% годовых при временной базе 360 дней и точным числом дней финансовой операции. Определить величину процентной ставки, обеспечивающей такой же процентный доход
а) при временной базе 365 дней;
б) при использовании приближенного количества дней финансовой операции.
15. Клиент поместил в банк 3 тыс. грн. 1 февраля. Процентная ставка банка с 1 февраля по 18 февраля – 7% годовых; с 19 февраля по 7 марта – 8% годовых; с 8 марта по 23 марта – 9% годовых; с 24 марта по 19 апреля, когда был изъят вклад - 10% годовых. Определите доход клиента и эффективную процентную ставку. Методика расчета: обыкновенные проценты с приближенным числом дней.
16. Клиент внес в сбербанк 3 тыс.грн. Согласно условиям договора «до востребования», процентная ставка может быть изменена банком в одностороннем порядке. Вклад внесен 3 апреля под 14% годовых. 22 апреля процентная ставка, согласно решению Правления банка, установлена в 15% годовых, а 20 мая – 13% годовых. Вклад вместе с процентами получен 3 июня. Определите наращенную сумму, если расчет процентов производится по точным процентам с точным числом дней в году (К=365).
17. Вкладчик заключил с банком депозитный договор на следующих условиях: сумма депозита 3 000 грн., срок 270 дней. Процентная ставка в первом квартале составляет 15%, во втором, третьем процентная ставка возрастает на 2,5%.Определить сумму полученную вкладчиком в конце срока депозита.
18. Коммерческий банк выдал кредит в размере 300 000 грн. на 3 года под 19% годовых. Через пол года процентная ставка была увеличена на 4,5%, еще через полгода заемщик погасил 150 000 основного долга, еще через год ставка была снижена до 21%. Определить сумму начисленных процентов и наращенную сумму.
Практическое занятие 3. Антисипативный метод начисления простых процентов
Цель: Изучить теоретические основы и получить практические навыки при расчетах по простым процентам антисипативным методом.
Антисипативный метод начисления предполагает, что проценты начисляются в начале временного интервала (удержание процента) исходя из наращенной суммы долга.
I = (FV-PV)*n= 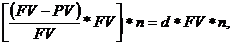
где 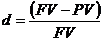 по определению учётной ставки
по определению учётной ставки
Наращение по простой учетной ставке производится по формуле
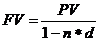 (3.1)
(3.1)
где FV – будущая стоимость или наращенная сумма;
PV – первоначальная сумма(стоимость);
n – срок операции;
d – простая учетная ставка.
Если срок операции не целое число, то 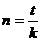
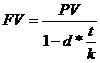
Дисконтирование – это расчетная операция обратная определению наращенной суммы, при которой определяется неизвестная первоначальная сумма PV, при известной наращиваемой сумме FV, при известном сроке финансовой операции и процентной ставке.
Операции дисконтирования необходимы при разработке условий финансовой сделки и при удержании процентов до наступления сроков погашения долга.
Существует 2 метода дисконтирования:
1 метод – Математическое дисконтирование:
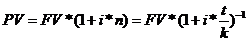
2 метод – Банковский учет
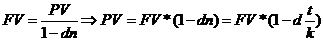
Другой весьма распространенной операцией краткосрочного характера, для оценки которой используются рассмотренные формулы, является операция по учету векселей банком. В этом случае пользуются учетной ставкой. Схема действий в этом случае может быть следующей: владелец векселя на сумму FV предъявляет его банку, который соглашается учесть его, т.е. купить, удерживая в свою пользу часть вексельной суммы, которая нередко также называется дисконтом. В этом случае банк предлагает владельцу сумму (PV), исчисляемую исходя из объявленной банком учетной ставки (d). Очевидно, что чем выше значение дисконтной ставки, тем большую сумму удерживает банк в свою пользу. Расчет предоставляемой банком суммы ведется по формуле, являющейся следствием формулы:
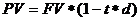
где t - относительная длина периода до погашения ссуды (отметим, что операция имеет смысл, когда число в скобках неотрицательно).
При учете векселя в банке до срока его погашения при сроке меньше года владелец векселя получит сумму, равную:
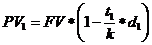
Наращенная сумма с учетом инфляции рассчитывается по формуле:
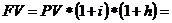
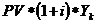
где h – темп инфляции;
Yk – индекс инфляции за k-периодов (Yk = (1+h1)*(1+h2)*…*(1+hk)).
Вопросы для обсуждения:
- стоимость денег и время;
- сущность дисконтирования;
- виды дисконтирования;
- учет векселей;
- наращение по учетной ставке.
Пример решения задачи
ПримерКлиент оформляет вклад на срочный депозит сроком на 1 месяц в коммерческом банке. Процентная ставка банка 6 % годовых. Годовой уровень инфляции 4,8%. Определите реальную годовую процентную ставку прибыли, по которой оформлен вклад.
Решение:
Годовая процентная ставка с учетом инфляции рассчитывается по
формуле:
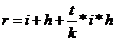
Отсюда реальная ставка доходности составит:
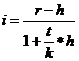
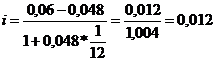
i = (0,06 – 0,048)/(1 + 1/12*0,048) = 0,18567.
Ответ: реальная ставка доходности по срочному депозиту составит 1,2% годовых.
Задачи
1. Определить величину суммы, выдаваемую заемщику, если он обязуется вернуть её через два года в размере 55000 грн. Банк определяет свой доход с использованием годовой учётной ставки 15 %.
2. Коммерческий банк выдал две ссуды 100 000 и 200 000 грн. под простой дисконт, равный 12% годовых и 13% годовых соответственно сроком на 2,5 года. Какую сумму банку необходимо выдать на руки одному и второму заемщику, какой доход получил банк?
- Клиенту необходимо получить кредит в размере 388 000 грн. на 6 месяцев. Банк предоставляет кредит под простой дисконт 20% годовых. Определить сумму полученного кредита.
- Предприятие намерено взять кредит в сумме 500 000 грн. Банк предоставляет кредит под:
а) 25 % простых годовых
б) простой дисконт 20 % годовых.
На какой срок фирма может взять кредит при условии, что подлежащая возврату сумма не должна превышать 900 000 грн.
5. Размер кредита, полученного фирмой на срок 6 месяцев, равен 600 тыс. грн. Сумма возврата кредита – 680 тыс. грн. Определите простую процентную и учетную ставку кредита.
6. Предприятие для модернизации оборудования решило взять в банке кредит в 600 тыс. грн. на условиях, что проценты простые и оплачиваются при выдаче кредита. Кредит выдается под 20% годовых. Срок кредита - 9 месяцев. Кроме того, банк требует 8% от суммы кредита в залог. Какую сумму получит заемщик. Определите реальную процентную ставку для кредита.
7. Фирма получила на полгода банковский кредит в 800 тыс. грн. под 24% годовых. Проценты за кредит банк берет авансом. Рассчитайте реальную процентную ставку за кредит в случае: а) не требуется залога, б) залог за предоставление кредита составляет 6% от суммы кредита.
8. Фирма получила кредит на 3 месяца под залог недвижимости стоимостью 16 тыс. грн. Величина кредита составляет 80% от стоимости недвижимости. Процентная ставка по кредиту - 36% годовых, комиссионные по обслуживанию кредита составляют 2%. Определите сумму полученного кредита, реальную процентную ставку и доход банка. Проценты за кредит банк берет авансом.
- Вексель номиналом 100 000 грн. выданный 1.06. на срок 3 месяца был учтен банком 20.06. по простой дисконтной ставке 20%. Определить сумму, полученную владельцем векселя.
- Вексель номиналом 1 тыс.грн. выдан 1 сентября на 1 год. Ставка процентов по векселю составляет 18 % годовых. Какой доход получит банк в результате учета 25 декабря векселя, учетная ставка которого составляет 14%. Методика расчёта точные проценты.
- Вексель номиналом 1 000 грн. сроком погашения через 180 дней был учтен банком за 45 дней до срока в сумме 925 грн. Определить учетную ставку банка.
- Долговое обязательство в сумме 2 тыс. грн. должно быть погашено через 90 дней с процентами 16% простых годовых был предъявлен в коммерческий банк для учёта. Владелец обязательства учел его в банке в сумме 1,999 тыс. грн. по учетной ставке 16%. Определите период, за который банк учел вексель.
- Банком был выдан кредит в размере 20000 тыс.грн. на 4 года под простую ставку 35% коммерческих годовых на условиях учета годового темпа инфляции. В первом году инфляция составила 5%, во втором - 7%, в третьем - 10%, в четвертом 15%. Определить сумму погашения.
- Депозит в сумме 55 000 грн. сроком на 6 месяцев под 7,5% простых годовых был привлечен банком на условиях учета темпа инфляции. За период цены выросли в 1,5 раза. По истечении 6 месяцев вкладчик продлил депозитный договор еще на 3 месяца на тех же условиях. Ожидаемый темп инфляции на данный период составляет: 8 % в первом месяце, 9,5% - во втором, 11,5% - в третьем. Определить доход клиента.
ТЕМА 3. РАСЧЕТЫ ПО СЛОЖНЫМ ПОЦЕНТАМ
Практическое занятие 4. Декурсивный метод начисления сложных процентов
Цель: Изучить теоретические основы и получить практические навыки при расчетах по сложным процентам декурсивным методом.
| Наращение | Дисконтирование |
| начисление %% 1 раз в году | |
| FV = PV*(1 + i) n | PV= FV / (1+ i) n |
| начисление %% m раз в году (промежуточные проценты) | |
| FV = PV*(1 + j/m) n*m | PV = FV / (1+ j/m) n*m |
Для упрощения расчетов разработаны таблицы финансовых коэффициентов. Множитель (1 + i) n ( или (1 + j/m) n*m ) называется множителем наращения., обозначается FVIFi, n или FVIFj/m, n*m от англ. Future Value Interest Factor.(Приложение В) Множитель 1/(1 + i) n ( или 1/(1 + j/m) n*m ) называется множителем дисконтирования, или дисконт-фактор. Обозначается РVIFi, n или РVIFj/m, n*m от англ. Present Value Interest Factor.(Приложение Б)
| Наращение | Дисконтирование |
| начисление %% 1 раз в году | |
| FV = PV* FVIFi, n | PV= FV / FVIFi, n = FV* РVIFi, n |
| начисление %% m раз в году (промежуточные проценты) | |
| FV = PV* FVIFj/m, n*m | PV = FV / FVIFj/m, n*m =FV* РVIFj/m, n*m |
Таким образом, можно сделать несколько простых практических выводов:
- при начислении процентов: 12% годовых неэквивалентно 1% в месяц;
- чем чаще идет начисление по схеме сложных процентов, тем больше итоговая накопленная сумма.
Заметим, что для простых процентов такие выводы недействительны.
Начисление процентов за дробное число лет. Достаточно обыденными являются финансовые контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться одним из двух методов:
а) схема сложных процентов:
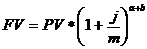
б) смешанная схема:
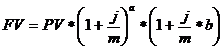
где а – целое число лет операции,
в – срок операции меньше года.
Непрерывное начисление процентов.
Все рассмотренные ранее начисляемые проценты называются дискретными, поскольку их начисление осуществляется за фиксированный промежуток времени (год, квартал, месяц, день, даже час). Уменьшая этот промежуток (период начисления) и увеличивая частоту начисления процентов, в пределе можно перейти к так называемым непрерывным процентам.
Формула наращения по непрерывной процентной ставке:
FV=PV*edn ,
где e – основание натурального логарифма е=2,718;
d - процентная ставка при начислении непрерывных процентов или сила роста;
edn - множителем наращения при непрерывной капитализации процентов.
Формула наращения с переменной силой роста:
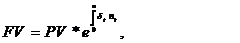 |
Формула наращения для случая, если сила роста изменяется дискретно:
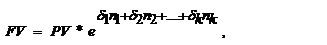 |
где d1,d2,….dк сила роста в соответствующих интервалах n1,n2,…nк.
Формула наращения для случая, если сила роста изменяется непрерывно и может быть описана арифметической прогрессией:
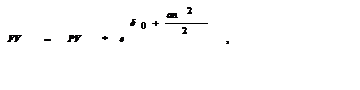 |
где d0- начальная величина силы роста;
a - годовой прирост или снижение силы роста.
Вопросы для обсуждения:
- начисление сложных процентов;
- понятие номинальной и эффективной ставки
- непрерывное начисление процентов;
- дисконтирование по сложным процентным ставкам;
- учет инфляции в финансовых операциях.
Примеры решения задач
Пример 4.1 Через два года фирме потребуются деньги в размере 30000 грн., какую сумму необходимо сегодня поместить в банк, начисляющий 15 % годовых, чтобы через 2 года получить требуемую сумму?
Решение:
Первоначальная сумма по известной будущей определяется по формуле:
PV= FV / (1+ i) n= 30000/(1+0,15)2=30000/1,3225=22684,4
Можно решить также с помощью таблиц множителей дисконтирования (Приложение Б)
PV= FV* РVIFi, n =30000*0,7561=22683 (грн)
Или с помощью таблиц множителей наращения (Приложение В)
PV= FV / FVIFi, n =30000/1,3225=22684,4 (грн)
Ответ: необходимо сейчас поместить в банк 22684, 4 грн., чтобы получить через 2 года 3000 грн.
Задачи
- Клиент положил в банк 8000 грн. Какая сумма будет на счете этого клиента а)через 1 год, б)через 8 месяцев, в)через 4 года, г)через 6 лет 6 месяцев, если банк начисляет:
· 6% сложных годовых ;
· банк начисляет проценты по ставке j3 = 6%.
- Определите наращенную сумму вклада в 3 тыс. грн. при сроке вклада 2 года по номинальной процентной ставке 16 % годовых. Начисление процентов производится: а) один раз в год, б) по полугодиям, в) поквартально, г) ежемесячно.
3. Какие условия предпочтет клиент при получении кредита:
а) процентная ставка - 20%, начисление процентов ежемесячное;
б) процентная ставка - 22%, начисление процентов ежеквартальное;
в) процентная ставка - 23%, начисление процентов по полугодиям.
4. Для строительства завода банк предоставил фирме кредит в 200 тыс.$ сроком на 10 лет из расчета 13% годовых. Проведите расчет коэффициента наращения, суммы начисленных процентов и стоимости кредита на конец каждого года.
- Банк выдал кредит в размере 75 000 грн. на 2 года и 170 дней под 25% сложных годовых. Определить, сумму к погашению и сумму начисленных процентов.
- Банк принимает вклады от населения по номинальной процентной ставке 12% годовых. Начисление процентов ежемесячное. Вклад 1200$ был изъят через 102 дня. Определите доход клиента.
7. Бабушка хочет, чтобы на счете у внука через 18 лет была сумма 30 000 грн. Определить, какую сумму ей необходимо внести сейчас в банк, если на вклад начисляется 15% сложных годовых.
- Г-н Иванов может вложить деньги в банк, выплачивающий проценты по ставке j6= 10%. Какую сумму он должен вложить, чтобы получить 20 000 грн. через 3 года 3 месяца?
- Г-н Петров хочет вложить 30 000грн., чтобы через 5 лет получить 40 000 грн. Под какую процентную ставку j12 он должен вложить свои деньги?
- Какой должна быть ми
