Возможно установление функциональной структуры организованного преступного сообщества, если функции его участников связаны с количеством их собственных (преступных) связей.

Введем также понятие отрицательных связей.К ним будем относить такие связи таких лиц, которые находятся в конфликтных отношениях (препятствуют достижению лицом его целей).

Предположим, что изменение числа связей будет происходить во времени по линейному закону, т.е. на графике такая зависимость будет представлять прямую линию.

Этот способ построения зависимости количества связей одного участника преступной группы от количества связей другого участника преступной группы соответствует детерминированному подходу к построению функциональных зависимостей. В основе этого подхода лежит принцип не случайности исходных данных, т.е. их детерминированности. Однако на практике не все преступные связи выявляются, кроме того, при выявлении связей могут быть допущены случайные ошибки или такие ошибки могут появиться вследствие дезинформации. Это означает, что исходные данные о преступных связях участников ОПГ будут представлять собой случайные числа. В этом случае детерминированный метод построения линейной зависимости становятся уже непригодным, т.к. он не позволяет описывать изменение среднего значения одной случайной величины от среднего значения другой случайной величины. Наиболее распространенным методом построения линейной функциональной зависимости для случайных величин, является линейная регрессия. Объясняется это тем, что математические модели, основанные на линейных зависимостях, наиболее просто реализуются на практике. При этом, несмотря на то, что множество явлений происходящих в реальной жизни следует отнести к нелинейным процессам, линейными моделями в том или ином приближении могут быть представлены большинство из них.

В основе регрессионного анализа лежит известный в статистике метод наименьших квадратов. В соответствии с этим методом близость найденной аналитической функции одного случайного числа от другого к исходной зависимости, определяется минимальным значением суммы квадратов их отклонений.

О степени близости полученной аналитической функциональной зависимости к детерминированной можно судить по множественному коэффициенту регрессии (коэффициент детерминированности). Если его значение близко к единице, то полученная функциональная зависимость близка к детерминированной функции.

Построим графики для линейных регрессионных зависимостей вида Sb=k*Sa+b и Sa=h*Sb+c. Отличие одной зависимости от другой будет заключаться в том, что в первом уравнении в качестве независимой переменной выступает переменная Sa, а в качестве зависимой Sb. Во втором уравнении все наоборот: - независимой переменной является Sb, а зависимой переменной Sa. Коэффициенты линейной функциональной зависимости k и h представляют собой углы наклона соответствующих графиков по отношению к горизонтальной оси. Свободные члены b и c в приведенных выше уравнениях дают фоновые значения этих функций и откладываются на соответствующих осях.

Для того чтобы построить графики линейных регрессионных зависимостей необходимо найти численные значения коэффициентов k и h , а также численные значения свободных членов b и c. Затем отложить значение b на оси Sb , а значение с на оси Sa. После этого провести через эти точки прямые линии под углами k и h относительно горизонтальной оси. Эти линии будут пересекаться в точке с координатами, соответствующими средним значениям числа связей лица A(координата Sa) и связей лица B(координата Sb).

Между линиями, построенными подобным образом, образуется угол, который характеризует степень близости исходных данных к случайным или детерминированным значениям. Если угол между линиями будет составлять 90 градусов, то это означает, что исходные данные являются случайными и между преступными связями лица A и лица B не существует функциональной зависимости. Если же между данными линиями угол составляет 0 градусов, то это свидетельствует, что исходные данные являются детерминированными и между преступными связями лица A и B существует строгая линейная функциональная зависимость. На рис. 4. приведены графики этих линейных регрессионных зависимостей для произвольных значений коэффициентов и свободных членов.

Sb

Sb=k*Sa+b

Sa=h*Sb+c

Sbср.

Sbлат.

b

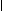Saср. 0 Saлат. c Sa

Рис. 4. Регрессионные зависимости функций у=f(x) и x=f(y).