Внутренняя доходность потока платежей

Для потока платежей {R₁, R₂,…, R_n}, совершаемых через одинаковые промежутки времени, с произвольными величинами и знаками при заданной процентной ставке r можно определить внутреннюю доходность IRR (Internal Rate of Return). Если выплаты производятся в конце периодов, то внутренняя доходность определяется решением IRR = r уравнения (NPV(R, r) = 0):

(11) R₁/(1 + r) + R₂/(1 + r)² + … + R_n/(1 + r)ⁿ = 0.

Если имеется выплата R₀в начале первого периода, то ее также учесть, добавив в левую часть уравнения без множителя.

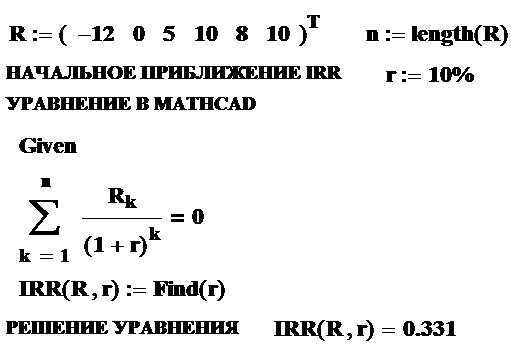Определим IRR с помощью программы Mathcad. На рабочем листе запишем данные задачи (поток платежей R), функцию для определения размера n вектора потока платежей R, начальное приближение неизвестного r, конструкцию [Given Уравнение Find] для решения уравнения в Mathcad, оператор присвоения полученного значения имени IRR. Получим решение IRR = 33.1%:

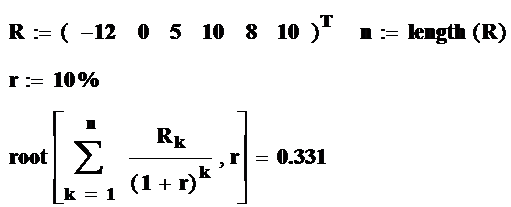Приведенный способ решения этого (и любого другого) уравнения является далеко не единственным. Например возможен следующий и многие другие варианты:

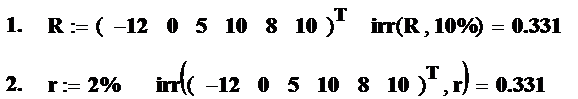В Mathcad 2000 и более поздних версиях имеется специальная финансовая функция irr, выполняющая те же вычисления без набора формулы и решения уравнения. Результат приводим в двух допустимых вариантах записи (комбинации этих вариантов также приемлемы):

Заметим, что начальные значения r во всех приведенных случаях могут быть различными. Однако, эти приближения должны быть выбраны из разумных соображений, поскольку для слишком далеких от истинных решений любого уравнения алгоритм решения может не сработать. Кроме того, если решение уравнения не является единственным, то найденное решение уравнения может зависеть от начального приближения. Кстати, неединственным может быть и решение уравнения (11) рассматриваемой задачи.

ПРИМЕРЫ РАСЧЕТОВ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ

МЕТОД КОМПАУНДИНГА

Рассмотрим пример сравнительной оценки инвестиционных проектов на основе компаундинга. Пусть имеется два альтернативных проекта со сроком окупаемости 5 лет. Проект А дает одинаковые доходы по годам, а проект Б требует вложений в первые годы, но дает большую отдачу в последующие годы. Размеры чистого дохода по годам обоих проектов приведены в таблице 5.

РАЗМЕРЫ ЧИСТОГО ДОХОДА ДВУХ ПРОЕКТОВ

Таблица 5

Годы	Проект А	Проект Б
		-110
Всего

Если сравнивать только суммы чистого дохода за 5 лет без учета сроков их получения, то более выгодным является проект Б.

Оценим теперь эти проекты с учетом того, что полученный доход можно пустить в рост под некоторый альтернативный процент по схеме сложных процентов. Аналогично можно было бы поступить и со средствами, которые инвестируются в проект Б. Суммы чистых доходов и их стоимость, приведенная ко времени окончания проектов, а также коэффициенты сложных процентов по годам приведены в таблице 6.