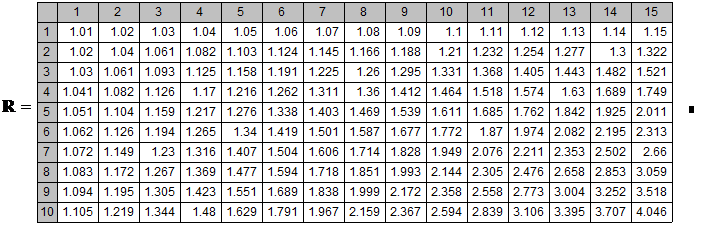
Коэффициенты сложных процентов

Таблица 1.

От периода к периоду базовая сумма, на которую начисляется процент, возрастает. Поэтому инвестор имеет доход как с первоначального капитала, так и с процентов, полученных за предыдущие периоды.

Приведем пример вычисления сложных процентов и построим график роста капитала для этого примера. Пусть первоначальный капитал PV=10 млн. руб., процентная ставка r=20%, время (число периодов) n меняется от 0 до 10. В таблице и на графике показан рост капитала.

РОСТ КАПИТАЛА ПРИ СЛОЖНЫХ ПРОЦЕНТАХ

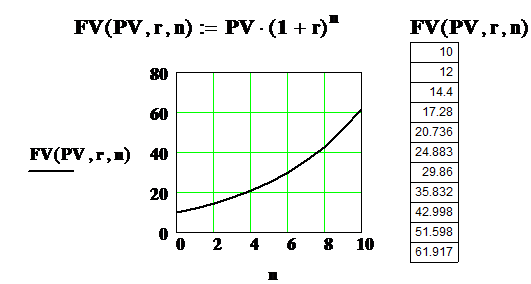
Начиная с версии Mathcad 2000 для вычисления будущей величины накопленной суммы по схеме сложных процентов нет необходимости выписывать формулу для вычисления сложного процента в явном виде. Среди набора финансовых функций имеется функция fv со следующим синтаксисом

fv(rate, nper, pmt, [[pv], [type]]),

где rate – процентная ставка, nper(number of periods) – количество периодов, составляющий срок кредита,pmt (payment)– величина периодических выплат или вкладов (в зависимости от знака + или - ). Аргументы функции, заключенные в прямоугольные скобки являются не обязательными и имеют значения, принятые по умолчанию. Аргументpv – начальный инвестированный капитал (знак +) или величина ссуды (знак -) (по умолчанию 0),type – параметр со значениями 1 или 0 (по умолчанию 0), в зависимости от того, в начале или в конце периода производятся периодические выплаты pmt.

Для ввода функции на рабочий лист программы следует в главном меню выбрать Insert (Ввести) – Function (Функция). Того же результата можно добиться, нажав кнопку со значком f(x) (Insert Function) на панели инструментов. В открывшемся диалоговом окне Insert Function в левом поле выбора Function Category выбрать категорию функций Finance(финансовые), а затем в появившемся в правом поле выбора Function Name в списке финансовых функций выбрать желаемую, то есть fv.

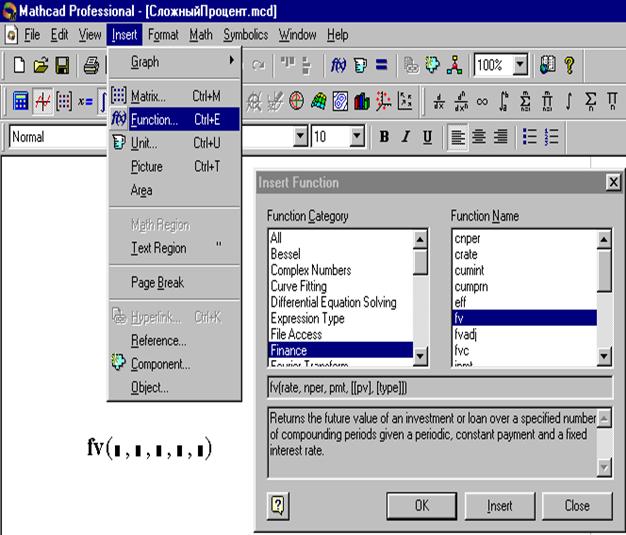
Ниже в строке синтаксиса указан правильный способ и порядок ввода аргументов выбранной функции и резюме назначения этой функции. Для ввода функции на рабочий лист нужно нажать кнопку Insertили OK. В обоих случаях на рабочем листе появится шаблон функции, с той лишь разницей, что в первом случае диалоговое окно не закроется, что позволит ввести в шаблон вместо черных прямоугольников аргументы функции, руководствуясь указанным синтаксисом, или выбрать еще какую-

либо другую функцию. Следует отметить, что выражение для любой функции со всеми аргументами можно ввести прямо с клавиатуры. Ниже в двух различных вариантах ввода аргументов приведены вычисления для рассматриваемой задачи. Знак минус перед значением соответствует инвестированию капитала.

МЕТОД ДИСКОНТИРОВАНИЯ

Метод дисконтирования денежных поступлений есть исследование денежного потока от будущего к текущему моменту. Другими словами, метод дисконтирования является обратным к методу компаундинга и состоит в приведении будущих доходов к сегодняшнему моменту времени. Он позволяет определить, сколько денег нужно вложить сегодня, чтобы получить определенную сумму через несколько периодов. Формула для метода дисконтирования является обратной к формуле компаундинга:

(4) PV = - FV / (1 + r)ⁿ.

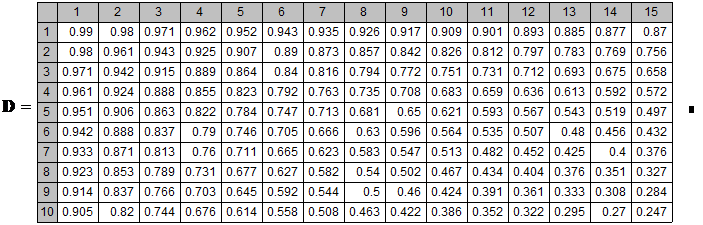
Величины D(r,n)=1/(1 + r)ⁿ называются коэффициентами дисконтирования. Ниже приведена таблица этих коэффициентов для различных r от 1% до 15% и n от 1 до 10.

КОЭФФИЦИЕНТЫ ДИСКОНТИРОВАНИЯ

Таблица 2.

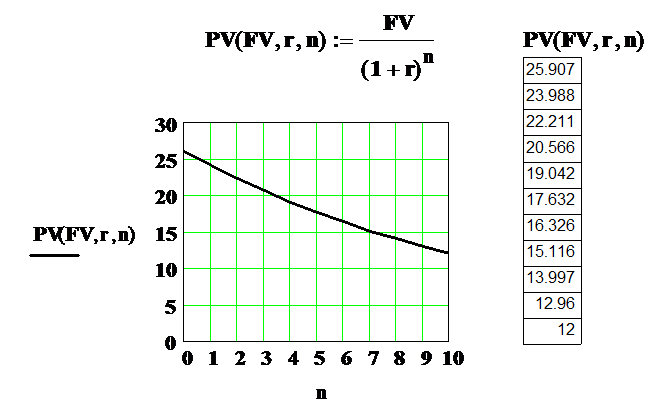
Приведем пример использования метода дисконтирования для вычисления начальных инвестиций и построим соответствующий график в Mathcad. Пусть инвестор через несколько лет хочет получить капитал FV=25.907 млн. руб., при процентной ставке r=8%. График зависимости PV (без учета знака) от времени n (число периодов n меняется от 0 до 10) показывает, сколько ему следует инвестировать сегодня для получения указанной суммы через n периодов (лет).

ВЫЧИСЛЕНИЕ НАЧАЛЬНЫХ ИНВЕСТИЦИЙ

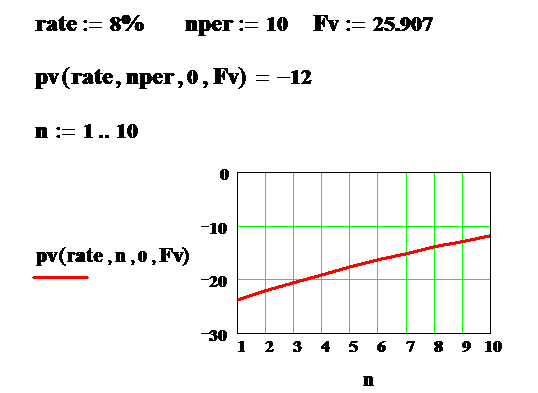
Также как и для вычисления сложных процентов начиная с версии Mathcad 2000 нет необходимости выписывать формулу для вычисления начальных вложений в явном виде. Среди набора финансовых функций имеется функция pv, действующая в соответствии со следующим синтаксисом

pv(rate, nper, pmt, [[fv], [type]]).

Устроена она совершенно аналогично с функцией fv, с той лишь разницей, что fv и pv меняются местами. Пример вычислений начальных инвестиций pv при заданной будущей возвращаемой сумме fv, процентной ставке за период rate и числу периодов nper приведен ниже. Там же построен график зависимости исходной суммы от срока вложений n, меняющегося от 1 до 10. Вычисления проведены с учетом знаков.

СТАНДАРТНЫЙ АННУИТЕТ

До сих пор мы рассматривали простейший финансовые потоки вида {- PV, FV } или { PV, - FV } с однократными взносами и выплатами. Однако не менее распространенными являются схемы денежных потоков с многократными взносами и выплатами через равные промежутки времени. Поток платежей { -PV, PMT, PMT,…, PMT, FV },все составляющие которого, кроме первого и последнего, имеют одинаковую величину и разделены равными промежутками времени, называется постоянной рентой. Формулу, приводящую все платежи к будущему, называют стандартным или будущим аннуитетом. Стандартный аннуитет основан на сложных процентах. Формула стандартного аннуитета имеет следующий вид:

(5) FVA_n,r = PMT ´ AF_n,r = PMT ´ [(1 + r)ⁿ -1]/r.

Если учесть первоначальный взнос, то конечная возвращаемая сумма будет равной

(6) FV_n,r = -PV(1+r)ⁿ + FVA_n,r = -PV(1+r)ⁿ + PMT ´ [(1 + r)ⁿ -1]/r.

Величина FVA_nназывается будущей стоимостью аннуитета. Величина PMT- разовый платеж в конце периода n. Коэффициенты AF_nr– будущая стоимость аннуитета в 1 рубль в конце каждого периода n при процентной ставке r.

Происхождение формулы легко понять, если сложить коэффициенты сложных процентов, начиная от 0 до n-1 включительно. Действительно, сумма коэффициентов сложных процентов за n периодов равна следующей геометрической прогрессии:

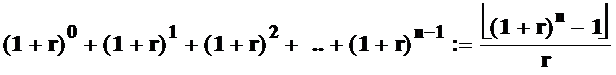
Приведем таблицу коэффициентов стандартного (будущего) аннуитета для n от 1 до 6 и r от 5% до 15%.

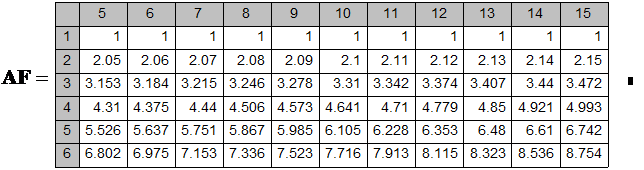
КОЭФФИЦИЕНТЫ БУДУЩЕГО АННУИТЕТА

Таблица 3.

Приведем пример вычисления по формулам будущего аннуитета. Первоначальный взнос составляет 300 денежных единиц, а затем 4 периода подряд вносится по 100. Процентная ставка – 8%. Накопленная сумма составит 858.758.

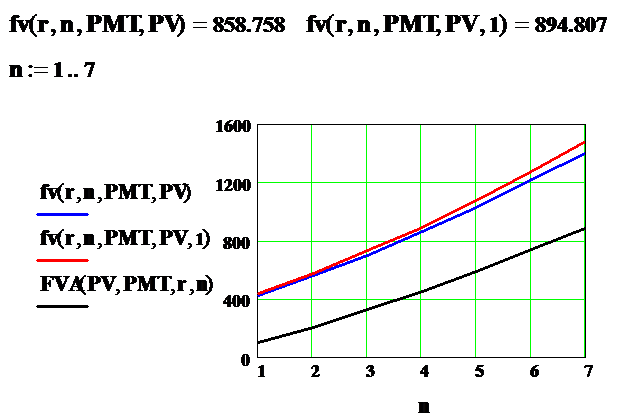
Вычислим величину будущих накоплений с помощью финансовой функции fvпрограммы Mathcad для счета постнумерандо (взнос в конце периода, пятый аргумент type функции fv равен 0 или опущен) и для счета пренумерандо (взнос в начале периода, пятый аргумент функции fv равен 1). Построим также графики роста накопленной суммы как функции количества периодов n для обоих случаев, а также график роста чистого будущего аннуитета FVA (нулевой начальный взнос PV=0).

ТЕКУЩИЙ АННУИТЕТ

Текущий аннуитет основан на дисконтировании и определяет сумму взносов (выплат, платежей), приведенную к настоящему времени с учетом процентной ставки. Формулы для вычисления текущего аннуитета имеет следующий вид:

(7) PVA_n,r = PMT ´ AP_n,r = PMT ´ [1-1/(1 + r)ⁿ]/r.

(8) PV_n,r = PV + PVA_n,r = PV + PMT ´ [(1 + r)ⁿ -1]/r.

Величина PVA_n,r – текущая стоимость будущих денежных поступлений при величине процентной ставки r, величине периодических платежей PMT и количестве периодов n. Формула (8) определяет приведенную сумму с учетом начальной суммы PV.

Коэффициенты AP_n,r = [1-1/(1 + r)ⁿ]/r – текущая стоимость аннуитета в 1 рубль в конце каждого периода n при ставке дохода r.

Эти коэффициенты являются суммами коэффициентов дисконтирования. Действительно, сумма коэффициентов дисконтирования за n периодов равна сумме следующей геометрической прогрессии:

Коэффициенты текущего аннуитета для n от 1 до 6 и r от 5% до 15% представлены в таблице 4.

КОЭФФИЦИЕНТЫ ТЕКУЩЕГО АННУИТЕТА

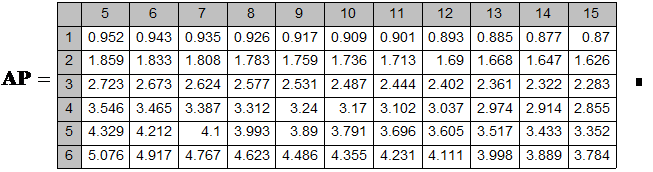
Таблица 4

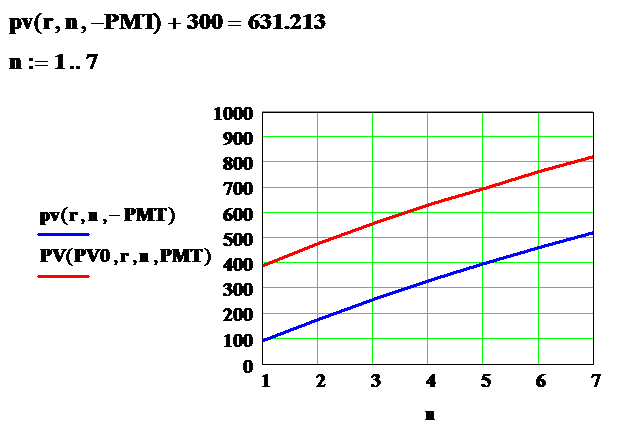
Рассмотрим тот же, что и в предыдущем пункте с точки зрения текущего аннуитета. Напомним, что первоначальный взнос составляет 300 денежных единиц, а затем 4 периода подряд вносится по 100. Процентная ставка – 8%. Накопленная сумма в соответствии со стандартным аннуитетом составила 858.758. Однако, эта же сумма, приведенная к настоящему времени, что видно из представленных вычислений составит всего 631.213 денежных единиц.

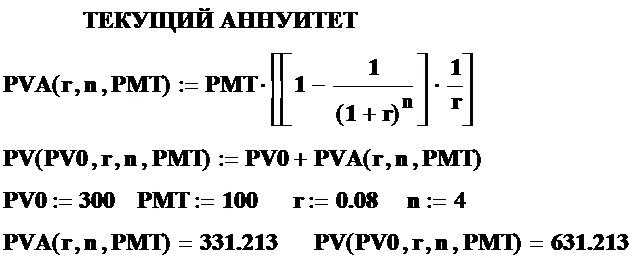
Вычисления будущего аннуитета с помощью финансовой функции pv программы Mathcad дают тот же результат, если учесть, что периодические взносы PMT должны быть подставлены в эту функцию со знаком минус. На графике приведены зависимости приведенной общей суммы накоплений и текущего аннуитета от количества периодов n, вычисленные по формуле и посредством использования финансовой функции pv.