Показатели качества регрессии

Коэффициент детерминации является одной из наиболее эффективных оценок адекватности регрессионной модели, т. е. мерой качества уравнения регрессии (соответствия регрессионной модели эмпирическим данным).

После построения выборочного уравнения регрессии, как уже указывалось выше, значение зависимой переменной y в каждом наблюдении можно разложить на две составляющие:

_i=y_i+e_i, i=1,n,

здесь остаток e_i представляет собой ту часть зависимой переменной y, которую невозможно «объяснить» с помощью выборочной регрессии. Можно показать, что выборочная дисперсия наблюдений y_i может быть представлена в виде суммы

, (1.2.1

в которой первое слагаемое представляет собой часть, «объясненную» регрессионным уравнением (или обусловленную регрессией), а второе слагаемое - «необъясненную» часть, характеризующую влияние неучтенных факторов и т. п. Необходимо заметить, что такое разложение справедливо только в том случае, когда в уравнение регрессии включена константа a, при этом

.

Разложение (1.2.1) часто записываю в следующем виде:

, (1.2.2)

где представляет собой общую сумму квадратов отклонений зависимой переменной от средней, есть сумма квадратов отклонений, обусловленная регрессией, а - остаточная сумма квадратов.

Коэффициент детерминации определяется по формуле:

. (1.2.3)

Величина R², как видно из формул (1) и (3), представляет собой часть (долю) вариации (разброса, дисперсии) зависимой переменной, обусловленную («объясненную») уравнением регрессии (иногда говорят - обусловленную вариацией объясняющей переменной).

Свойства коэффициента детерминации:

Свойство 1. 0 R²1;

Свойство 2. Чем ближе R² к единице, тем лучше регрессия аппроксимирует эмпирические данные, т. е. эмпирические наблюдения ближе к линии выборочной регрессии. Если R²,=1 то между x и y есть линейная функциональная зависимость, в этом случае все эмпирические точки наблюдений лежат на прямой регрессии;

Свойство 3. Если R²,=0 то в этом случае вариация зависимой переменной полностью обусловлена случайными воздействиями и линия выборочной регрессии параллельна оси Ox.

Заметим, что коэффициент детерминации R² имеет смысл рассматривать только при наличии свободного члена в уравнении регрессии, так как лишь в этом случае справедливо равенство (1.2.1).

Оценка качества соответствия выборочного равнения регрессии наблюдаемым данным может производиться и с помощью средней ошибки аппроксимации регрессии по формуле: (1.2.4)

Как указывают некоторые авторы, в практических исследованиях значение этой ошибки в пределах 5-7 % свидетельствует о хорошем соответствии модели эмпирическим данным.

Коэффициент регрессии b, как уже отмечалось выше, показывает, на сколько единиц в среднем изменяется значение показателя y, когда фактор x увеличивается на одну единицу, поэтому он также может служить мерой тесноты связи между x и y. Однако b зависит от единиц измерения переменных. Именно поэтому удобно использовать некоторую «стандартную» систему единиц измерения тесноты связи, в которой различные данные были бы сравнимы между собой. В качестве единиц измерения такой системы используется среднее квадратическое отклонение переменных, а показателем тесноты связи служит коэффициент корреляции.

Действительно, используя понятия выборочных дисперсий, ковариации и корреляции, оценки МНК можно записать специальным образом:

, ,(1.2.5)

где , - выборочные средние, , - выборочные дисперсии, r_xy- выборочный коэффициент корреляции (см. (1.2.5)).

Следовательно, парная эмпирическая линейная регрессия может быть записана в виде . (1.2.6)

Таким образом, величина

(1.2.7)

показывает, на сколько величин Sy изменится (в среднем) y, если x увеличится на одно s_x, поэтому выборочный коэффициент корреляции r_xy также является показателем тесноты связи (более точно - характеризует тесноту линейной зависимости) между переменными.

Выборочный коэффициент корреляции является безразмерной величиной и обладает следующими свойствами:

Свойство 1. -1 r_xy1;

Свойство 2. При r_xy =  1 корреляционная зависимость представляет собой линейную функциональную зависимость (все наблюдаемые значения располагаются на прямой линии регрессии);

Свойство 3. При r_xy = 0 линейная корреляционная связь отсутствует (линия регрессии параллельна оси Ox).

Заметим, что выборочный коэффициент корреляции r_xy полностью оценивает тесноту связи только в случае совместного нормального распределения случайных величин x и y, в других случаях выборочный коэффициент корреляции является оценкой меры только линейной зависимости.

Практически наиболее удобна следующая формула вычисления r_xy (которая непосредственно может быть получена из определения):

3.

(1.2.8)

В случае парной линейной регрессии между коэффициентом детерминации R²и коэффициентом корреляции r_xy существует следующая связь:

² = r²_xy^. (1.2.9)

F-тест качества спецификации множественной регрессионной модели.

Статистикой обсуждаемого ниже критерия гипотезы H₀: R²=0 (гипотеза о том что модель абсолютно плохая) против альтернативы H₁: служит случайная переменная:

Здесь k — количество регрессоров в модели множественной регрессии, п — объем обучающей выборки (у, X), по которой оценена МНК-модель. В ситуации, когда гипотеза H₀ справедлива, а случайный остаток и в модели обладает нормальным законом распределения, случайная переменная F_тест имеет распределение Фишера с количествами степеней свободы ν₁ и ν₂, где ν₁=k и ν₂=n-(k+1) (2)

Данное утверждение положено в основу F-теста. Вот этапы выполнения этой процедуры.

1) вычислить величину (1);

2) задаться уровнем значимости а ? (0, 0,05] и при помощи
функцииFPACПOБPExcel при количествах степеней свободы (2) отыскать (1-α)-квантиль распределения ФишераF_крит

3) проверить справедливость неравенства F<F_крит (3)

Если оно справедливо, то принять гипотезу H₀ и сделать вывод о неудовлетворительном качестве регрессии, т.е. об отсутствии какой-либо объясняющей способности регрессоров в рамках линейной модели.

Напротив, когда неравенство (3) несправедливо —следует отклонить гипотезу H₀ в пользу альтернативыH₁. Другими словами, сделать вы

Дисциплина «Эконометрика» Б1.Б.13

3) вопрос:Построение моделей множественной регрессии. Статистическая оценка качества уравнений. ПК-4, ПК-8

Ответ:

Когда невозможно описать модель с помощью одного фактора, вводят другие факторы, то есть строят модель множественной регрессии:

y= a+ b₁x₁ … + b_px_p + e

Пример: Функция потребления – Потребление зависит от дохода, цен, наличных денег, ликвидных активов.

Шаг первый: Выбор спецификации модели. Включает в себя два вопроса: a). выбор факторов и b). выбор вида уравнения регрессии

(Это еще и 15-й вопрос)

a) Очевидно, что включаемые факторы должны описывать модель. 2 требования к выбираемым факторам:
- они должны быть Количественно Измеримыми (либо дать им количественную определенность)

- факторы не должны коррелировать между собой (r_x1x2=0). Иначе неустойчивость и ненадежность оценок коэффициентов регрессии

Для модели, включающей N факторов рассчитывается показатель детерминации R², который фиксирует долю объясненной вариации результативного признака за счет тех самых N факторов.

Влияние неучтенных факторов – это (1-R²)

Лишние факторы, статистически незначимые или дублирующие (с коэффициентом внутренней корреляции выше 0,7), выбрасываются из модели

При выявлении двух коллинеарных факторов один из них выбрасывается, при чем предпочтение отдается тому, чья связь с прочими факторами меньше.

Отбор факторов производится на основе теоретико-экономического анализа, но он не рассматривает количественную взаимосвязь признаков => ОТБОР ПРОВОДЯТ В 2 ЭТАПА:
1 – отбираются факторы, исходя из проблемы (логически)

2 – на основе матрицы показателей корреляции и определения t-статистики (значимости факторов) для параметров регрессии

Матрица парных коэффициентов корреляции:

	Y	X1	X2	X3
Y
X1	Ryx1
X2	Ryx2	Rx1x2
X3	Ryx3	Rx1x3	Rx2x3

Здесь появляется проблема мультиколлинеарности, которая относится к вопросу 23. Мультиколлинеарность факторов – ситуация, когда больше 2х факторов связаны между собой линейной зависимостью => невозможно оценить воздействие каждого фактора в отдельности.

Мультиколлинеарность – это плохо потому, что: 1 – затрудняется интерпретация факторов; 2 – оценки параметров ненадежны => модель непригодна для анализа и прогноза

Симптомы мультиколлинеарности:

1) завышенное значение коэффициента детерминации (чем ближе к 1, тем сильнее мультиколлинеарность). Сравнивая коэффициенты можно найти факторы, ответственные за Мультикол-ть

2) высокие стандартные ошибки для коэффициентов регрессии

3) широкие доверительные интервалы

4) низкое значение t-критерия

5) появление при коэффициентах регрессии знаков, противоположных ожидаемым

6) Значительное изменение параметров модели при незначительном уменьшение кол-ва наблюдений.

Меры по устранению мультиколлинеарность:

1) удаление из модели переменных с высоким коэффициентом парной корреляции между факторами, если это не противоречит теории, положенной в основу построения модели

2) увеличение числа наблюдений

3) изменение функциональной формы модели

4) функциональное преобразование тесно связанных м/у собой факторов. Например, факторы площадь и население заменить на один фактор – плотность населения.

5) Переход к уравнениям приведенной формы – в ур-ие регрессии подставляют рассматриваемый фактор, выраженный из другого ур-ия

6) Построение моделей по отклонению от средней величины

7) использование специальных методов обработки временных рядов

Парные коэффициенты не в полной мере решают вопрос выбора факторов. Матрица частных коэффициентов корреляции более точная или же используется t-критерий Стьюдента для исключения факторов с величиной t-критерия меньше табличного.

При отборе факторов рекомендуется использовать в 6-7 раз меньше факторов, чем объем совокупности, тогда F-критерий не будет меньше табличного.

Выявить мультиколлинеарность можно с помощью матрицы парных коэффициентов корреляции. Если определитель матрицы = 1, то связь м/у факторами полностью отсутствует, если он = 0, то связь близкая к функциональной. Итог: чем ближе определитель к 1, тем лучше.

После того как уравнение регрессии найдено, проводится оценка значимости как уравнения в целом, так и его отдельных параметров.

Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. Согласно F-критерию Фишера, выдвигается «нулевая» гипотеза H0 о статистической незначимости уравнения регрессии и показателя тесноты связи.

Непосредственному расчету F-критерия предшествует анализ дисперсии.

Наблюдаемые значения результативного признака yi можно представить в виде суммы двух составляющих ŷi и εi:

yi = ŷi+ εi

Из данного уравнения следует следующее соотношение между дисперсиями наблюдаемых значений переменной D(y), ее расчетных значений D(ŷ) и остатков D(е) (остаточной дисперсией Dост = D(ε)):

D(y) = D(ŷ) + D(ε)

= +

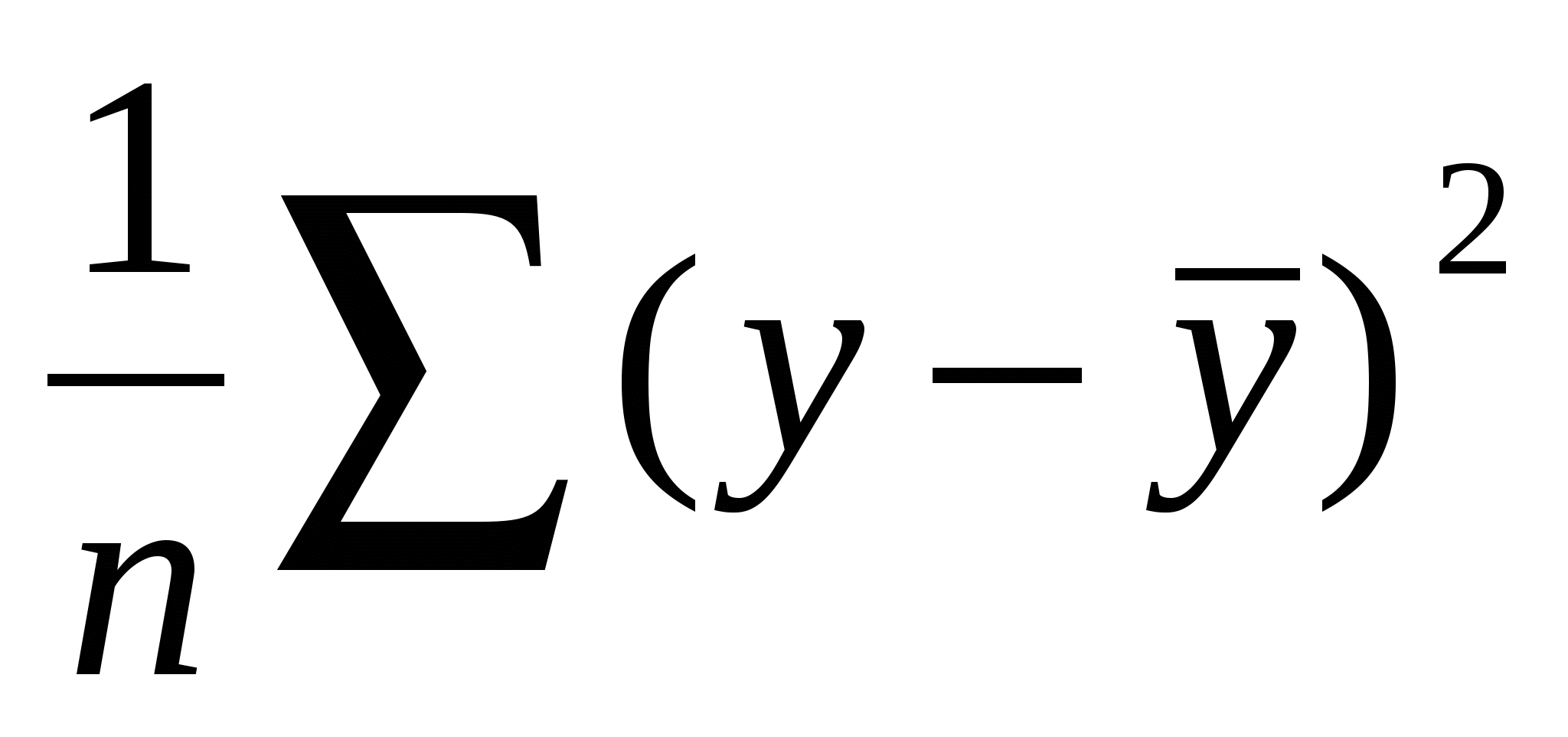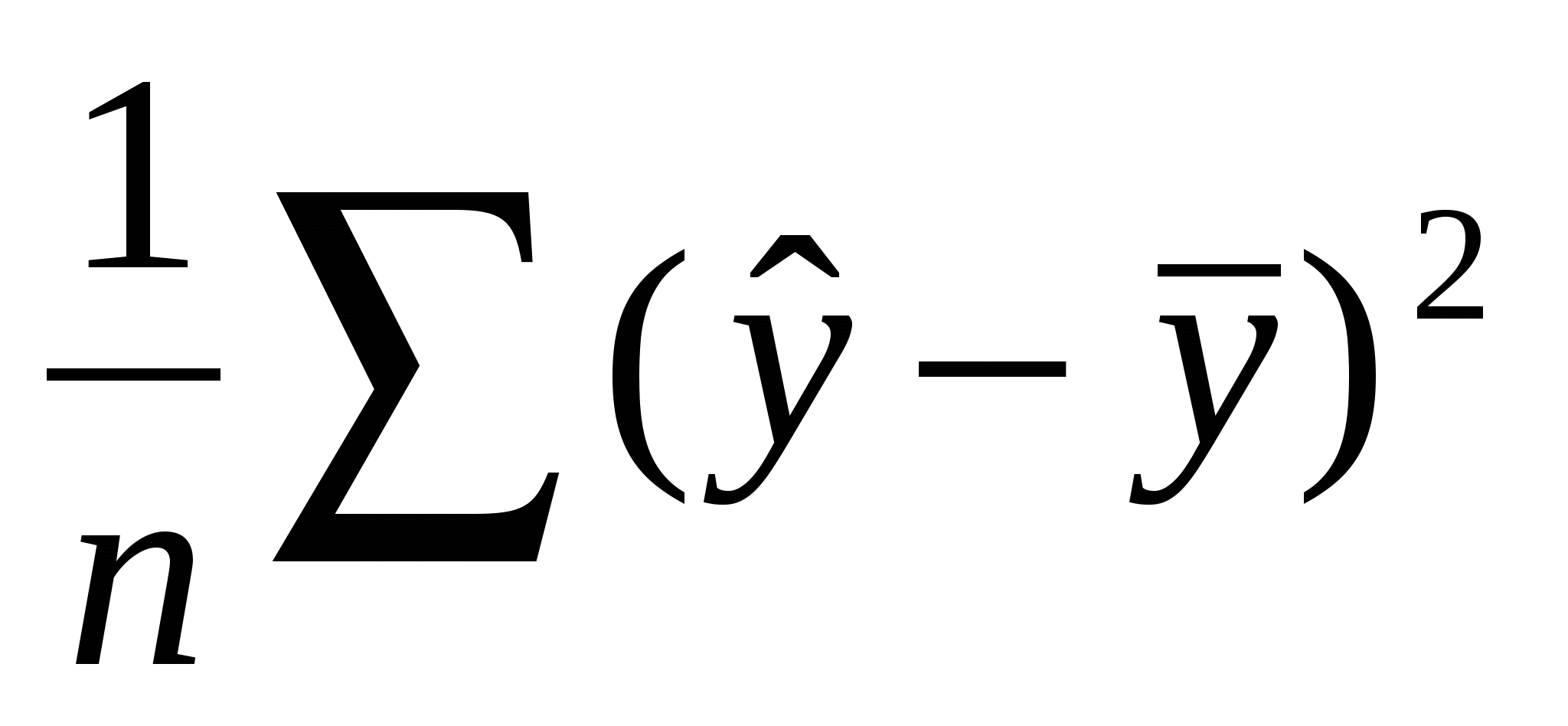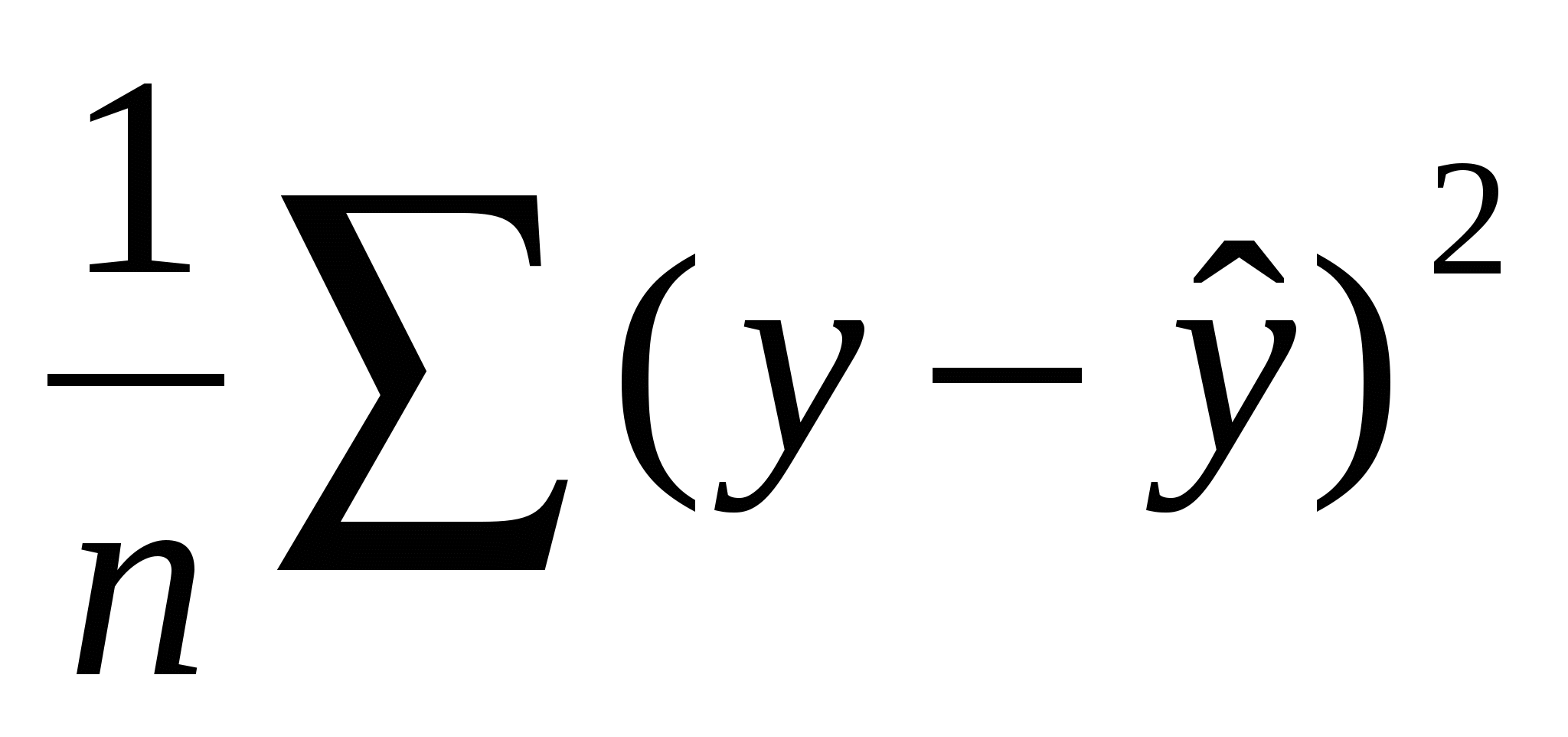
полная (общая) сумма квадратов отклонений

=

сумма квадратов отклонений, объясненная регрессией

+

(остаточная) сумма квадратов отклонений, не объясненная регрессией

(слайд 12)

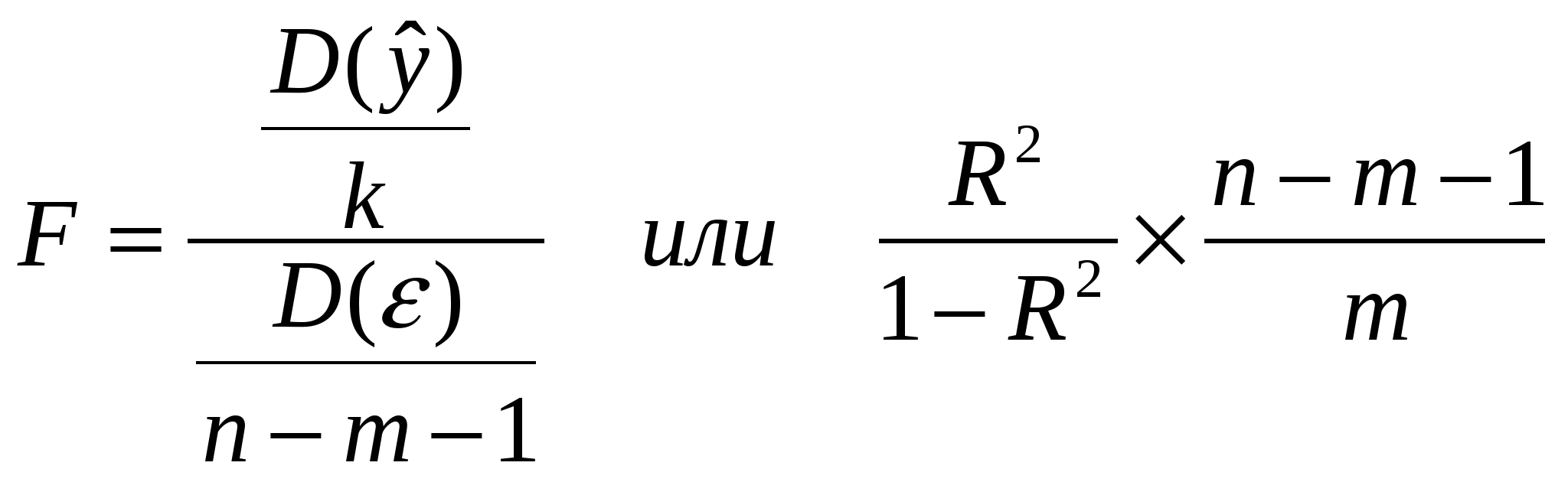
где m– число независимых переменных в уравнении регрессии (для парной регрессииm= 1);

n – число единиц совокупности.

Если нулевая гипотезаН0 справедлива, то факторная и остаточная дисперсии не отличаются друг от друга (т. е. отличие величины F от нуля статистически незначимо).

Если нулевая гипотеза Н0 не справедлива, то факторная дисперсия превышает остаточную в несколько раз.

4) вопрос:Расчет производственной функции Кобба-Дугласа. ПК-2. ПК-4. ПК-8

Ответ: Производственная функция – это зависимость между набором факторов производства и максимально возможным объемом продукта, производимым с помощью данного набора факторов. Производственная функция всегда конкретна, т.е. предназначается для данной технологии. Новая технология – новая производительная функция. С помощью производственной функции определяется минимальное количество затрат, необходимых для производства данного объема продукта.

Производственные функции, независимо от того, какой вид производства ими выражается, обладают следующими общими свойствами:

1) Увеличение объема производства за счет роста затрат только по одному ресурсу имеет предел (нельзя нанимать много рабочих в одно помещение – не у всех будут места).

2) Факторы производства могут быть взаимодополняемы (рабочие и инструменты) и взаимозаменяемы (автоматизация производства).

В наиболее общем виде производственная функция выглядит следующим образом:

,

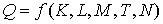где 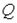- объем выпуска;

K- капитал (оборудование);

М- сырье, материалы;

Т – технология;

N – предпринимательские способности.

Наиболее простой является двухфакторная модель производственной функции Кобба – Дугласа, с помощью которой раскрывается взаимосвязь труда (L) и капитала (К). Эти факторы взаимозаменяемы и взаимодополняемы. Еще в 1928 году американские ученые — экономист П. Дуглас и математик Ч. Кобб — создали макроэкономическую модель, позволяющую оценить вклад различных факторов производства в увеличении объема производства или национального дохода. Эта функция имеет следующий вид:

Q=AK ^α *L ^β ,

где А – производственный коэффициент, показывающий пропорциональность всех функций и изменяется при изменении базовой технологии (через 30-40 лет);

K, L- капитал и труд;

α,β -коэффициенты эластичности объема производства по затратам капитала и труда.

Если α = 0,25, то рост затрат капитала на 1% увеличивает объем производства на 0,25%.

На основе анализа коэффициентов эластичности в производственной функции Кобба - Дугласа можно выделить:

1) пропорционально возрастающую производственную функцию, когда

α+ β=1 ( ).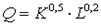

2) непропорционально – возрастающую

);

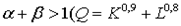3) убывающую

.

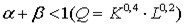Рассмотрим короткий период деятельности фирмы, в котором из двух факторов переменным является труд. В такой ситуации фирма может увеличить производство за счет использования большего количества трудовых ресурсов. График производственной функции Кобба – Дугласа с одной переменной изображен на рис. 1 (кривая ТР_н ).

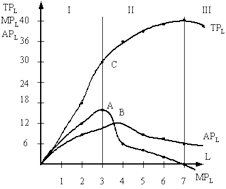
Рис. 1. Динамика и взаимосвязь общего среднего и предельного продуктов

дисциплина «Бухгалтерский учет и анализ» Б1.Б.16