Абсолютный и относительный методы

ОПИСАНИЯ ПОРТФЕЛЯ

Простейший способ описания портфеля состоит в указании количества активов того или иного вида, входящих в портфель. То есть, если

-

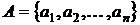полный перечень активов рынка, то портфель можно задать как вектор

, (7)

где - количество единиц актива , входящего в портфель.

Если - начальный капитал, а - начальная цена единицы актива , то необходимо выполнение условия

,

где - стоимость актива , то есть

. (8)

Описание портфеля с помощью структурного вектора (7) с условием (8) можно назвать абсолютным методом. Однако чаще применяется относительный метод описания портфеля, когда он задается вектором относительных весов каждого актива:

, (9)

где , то есть:

. (10)

Здесь условие (10) называют основным ограничением, которому удовлетворяет вектор, представляющий портфель.

Например, в № 3 портфель имел вид .

Отметим также, что любой вектор можно разложить по базисным векторам (ортам) , , … , , в виде:

.

В частности, вектор из № 3 будет выглядеть как:

.

ХАРАКТЕРИСТИКИ ПОРТФЕЛЯ

Так как портфель состоит из различных активов, то есть является своеобразным «составным» активом, то для него можно ввести все характеристики, установленные выше для активов.

Если доходности (реализованные) активов равны , то реализованная доходность всего портфеля будет равна:

.

Если же доходности активов рассматривать как случайные величины , то доходность портфеля как случайной величины, будет равна

, (11)

что позволяет получить вероятностные характеристики портфеля:

- (12)

ожидаемая доходность портфеля;

, (13)

или

- (13’)

ожидаемый риск портфеля.

Последняя формула следует из свойств дисперсии:

,

.

И если обозначить через - вектор ожидаемых доходностей активов, то

, (12’)

где - скалярное произведение векторов;

, (7”)

где

-

произведение ковариационной матрицы С, на вектор-столбец ( - вектор-строка).

Или в матричной форме:

, .

№ 5. Вычислить характеристики портфеля в условиях № 3.

Решение. Так как

, ,

,

то

,

.

То есть мы получили те же самые значения, но с использованием понятий матричной алгебры.

ВИДЫ ПОРТФЕЛЬНЫХ СТРАТЕГИЙ

Из определения относительных весов

,

можно сделать вывод, что для всех активов , или . Портфель такого вида называют стандартным, или говорят, что инвестор находится по каждому активу в длинной (long) позиции. Обычно это означает, что инвестор за счет своих средств покупает актив с целью его последующей продажи (закрытие позиций). Такая покупка совершается при ожидании повышения цены актива, что позволяет инвестору получить доход от разности цен покупки и продажи актива.

Однако, если инвестор относительно некоторого актива уверен в понижении его стоимости, то он может совершить сделку, называемую короткой продажей (short sale). Для этого он берет данный актив взаймы у другого инвестора, сразу же продает его, а потом покупает его по сниженной цене и возвращает его своему кредитору. Теоретически доходность такой операции может быть бесконечно большой, так как не требует никакого начального капитала; но зато и риск ее теоретически бесконечен, так как при повышении цены на такой актив, инвестор вынужден покупать его уже по более высокой цене.

Инвестор, осуществив короткую продажу, может на вырученные деньги купить и другие активы, что приводит к перераспределению стоимости активов (весов) портфеля. Пусть начальный капитал был равен , стоимость проданного (с короткой позиции) актива равна , тогда весь его капитал составит величину . На эту сумму он покупает активы 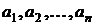, затратив при этом на актив сумму . Тогда

,

или

.

Разделив обе части этого равенства на , получим:

,

где . И если ввести обозначение , то снова будет справедливым условие (10):

.

То есть портфель инвестора снова описывается с помощью вектора с основным ограничением (10), только некоторые компоненты этого вектора могут быть отрицательными.

Следует отметить, что хотя короткие продажи вполне допустимы на большинстве фондовых бирж запада, но в виду особой рискованности таких операций, могут вводиться ограничения на общую величину коротких позиций в сделках. Другими словами на компоненты вектора могут накладываться определенные ограничения, и портфель, удовлетворяющий этим ограничениям (условиям данного рынка) называется допустимым. Такие портфели и будем рассматривать в дальнейшем.