Ковариация и корреляция активов

Предположим теперь, что в условиях задачи № 1 инвестору доступен рынок, состоящий только из активов и . Тогда решить двухкритериальную задачу (3) не представляется возможным, так как большей доходностью обладает актив (10% против 7,5%), а меньшим риском обладает актив (11,45% против 15%).

В этом случае инвестор вместо выбора одного актива, скорее всего, составит портфель из обоих активов, стремясь перераспределить (диверсифицировать) риск с целью уменьшения его количественной оценки. Степень возможности такой диверсификации зависит от характеристики, служащей мерой зависимости между случайными величинами. В качестве такой характеристики можно использовать ковариацию или коэффициент корреляции.

Известно, что ковариация между случайными величинами и определяется как

, (4)

а коэффициент корреляции как

, (5)

причем , .

Положительное значение ковариации показывает, что доходности ценных бумаг имеют тенденцию изменяться в одну сторону. Отрицательная ковариация показывает, что доходности имеют тенденцию компенсировать друг друга. Относительно небольшое или нулевое значение ковариации показывает, что связь между доходностями соответствующих ценных бумаг слаба (незначима), либо отсутствует вообще.

№ 2. Составить ковариационную и корреляционную матрицы в условиях № 1.

Решение. Составим сначала законы распределения двумерных случайных величин , , . Например:

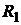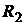	0,3	-	-
	-	0,6	-
-20	-	-	0,1

Тогда:

,

.

Аналогично:

, ;

, .

Полученные данные записывают обычно в матричном виде, составляя ковариационную и корреляционную матрицы:

,

.

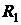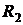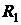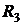Из полученных результатов видно, что доходности и изменяются в «одном направлении» ( ), а доходности , и 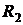, 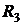– изменяются в «противоположном направлении» ( , ). Отрицательная корреляция между доходностям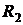и и 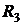позволяет строить портфель, состоящий из активов и с меньшим риском, чем у портфеля, состоящего только из актива или .

№ 3.Найти доходность и риск портфеля, сформированного на 50% из активов и на 50% из активов .

Решение. Определим стоимость портфеля (в условных единицах) для каждого из состояний рынка с учетом ожидаемой доходности:

а) для 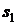: у.е.;

б) для 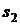: у.е.

в) для 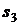: у.е..

Тогда доходы будут соответственно равны: , , .

Распределение доходности в этом случае имеет вид:

		-2,5
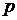	0,3+0,6=0,9	0,1

То есть:

%,

а дисперсия будет равна:

,

и

%.

Следовательно, доходность смешанного портфеля выше, чем доходность портфеля, состоящего из актива (на 1,25%) и меньше доходности портфеля, состоящего из актива (на 1,25%). Но риск при этом уменьшился по сравнению с активом более чем в 3 раза, а по сравнению с активом в 4 раза.

Другими словами, при достаточно небольшом снижении доходности (по сравнению с активом ), удалось значительно снизить риск.

Можно решить эту задачу и в более общем виде, когда портфель формируется на % из актива и на % из актива .

Если же в условиях № 1 инвестору предлагается сделать однозначный выбор между двумя вариантами вложения капитала (или в актив 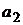, или в актив 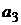), один из которых (актив 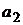) характеризуется одновременно и большей доходностью и большим риском, то часто используется особая мера риска – коэффициент вариации:

.

Этот коэффициент отражает риск, который приходится на единицу доходности. Он дает базу для сравнения вариантов инвестирования, когда и их средняя доходность и их риск неодинаковы.

В нашем случае:

, ,

то есть по этому критерию уровни риска активов 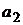и 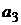практически одинаковы.