Принятие прогнозных управленческих решений

В УСЛОВИЯХ РЫНОЧНОЙ НЕОПРЕДЕЛЕННОСТИ

Математический инструментарий для выработки прогнозных

Решений в условиях неопределенности

Как ранее было отмечено, при решении многих задач управления и прогнозирования (планирования) проблема принятия решений резко усложняется из-за влияния различного рода случайных факторов, к которым чаще всего относятся условия проведения операции (климат, горно-геологические условия), надежность оборудования, опыт и квалификация персонала и т.п.). Естественно, что в таких условиях принятие решения достаточно сложно из-за неопределенности, возникающей либо от недостатка (отсутствия) информации, либо от неоднозначности целей, стоящих перед решаемой проблемой. Точные математические методы в таких ситуациях не всегда приводят к желаемому результату. Однако использование экономико-математических методов теории игр и статистических решений позволяет глубже разобраться в задаче и свести к минимуму элементы риска и волюнтаризма [49].

Теория игр используется для анализа конфликтных ситуаций, в которых противодействуют (обычно активно) различные стороны (об этом речь пойдет далее). Теория статистических решений принимается в ситуациях, когда неопределенность в условиях отсутствия активного противника, противодействующего намерениям ЛПР. Роль такого условного противника часто выполняет природа, являющаяся условием, поведение которого неизвестно, хотя элемент явного противодействия отсутствует. Поэтому подобные ситуации называются "играми с природой".

Рассмотрим общую постановку задач теории статистических решений.

Имеется несколько вариантов решения какой-либо управленческой задачи (А₁, А₂ … А_m). Эффективность каждого варианта, помимо известных факторов, определяется также рядом факторов (условий), точное значение которых неизвестно (климат, спрос на продукцию, цены на оборудование в перспективе и т.д.). Определенным предположением о значениях (состоящих) случайных факторов – состояния природы П₁, П₂,… П_n – соответствуют различные показатели вариантов решения задачи a_ij при использовании варианта i и состояния природы j. Показатели для различных вариантов решений (стратегий, альтернатив) А_i при возможных состояниях природы П_j задаются матрицей ||a_ij||, которую называют платежнойили матрицей выигрышей (ожидаемых исходов) (табл. 3.1).

Таблица 3.1.

Платежная матрица

Стратегия	Состояние природы
П1	П2	…	Пj	…	Пn
А1	a11	a12	…	a1j	…	a1n
А2	a21	a22	…	a2j	…	a2n
…	…	…	…	…	…	…
Аi	ai1	ai2	…	aij	…	ain
…	…	…	…	…	…	…
Am	am1	am2	…	amj	…	amn

Требуется найти такое решение, то есть такую стратегию А_i, которая предпочтительней по сравнению с остальными альтернативами.

Часто для решения подобных задач используют матрицу рисков (сожалений) - ||r_ij||, которая может дать более наглядную картину для вариантов действий. Риск r_ij представляет собой разность между максимальным выигрышем при определенном состоянии природы П_j и выигрышем, полученным при использовании стратегии A_i:

r_ij = b_j - a_j, (3.1)

где

b_j = max a_ij. (3.2)

Выбор варианта решения начинают с сопоставления стратегий, выявляя, не имеется ли стратегий лучших при любых состояниях природы – доминирующих.

Выбор решения тривиален, если одна стратегия доминирует над остальными. Если же доминирующие стратегии отсутствуют, то в зависимости от состояния природы (которое неизвестно) эффективны и различные варианты решений. В подобных случаях для принятия решения целесообразно воспользоваться различными критериями оптимальности.

1. Математическое ожидание выигрыша. Используется тогда, когда имеется информация о вероятностях состояния природы P_j, причем 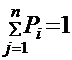. Критерием в этом случае выступает математическое ожидание выигрыша (или риска), то есть выбирается решение, при котором

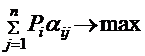(3.3)

или

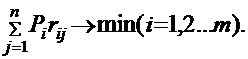(3.4)

2. Критерий Лапласа. Применяется в случаях, когда вероятности состояния природы неизвестны и их нельзя получить с достаточной точностью, но при этом предполагается, что состояние природы равновероятно, т.е.

Р₁=P₂=…=P_n. (3.5)

3. Критерий Байеса.Этот метод основан на последовательном пересчете вероятностей состояния природы (апостериорных вероятностей) в зависимости от прошлых (или принятых ранее) состояний (априорных вероятностей).

4. Максиминный критерий Вальда. Для каждой стратегии находят минимальное значение выигрыша, соответствующее наихудшему состоянию природы, т.е. min a_ij. Далее из всех возможных стратегий выбирается та, для которой минимальный выигрыш максимален:

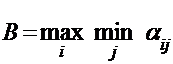
(3.6)

Критерий Вальда пессимистичен, так как он ориентируется на наихудшее состояние природы, то есть по существу природа рассматривается как активно противоборствующий противник.

5.Минимаксный критерий Сэвиджа– также вариант пессимистического подхода. В этом случае находят минимальное значение риска при самом неблагоприятном состоянии природы

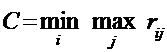. (3.7)

С этой целью для каждой стратегии (построчно) по матрице рисков находят максимальное значение риска, а затем выбирают из них минимальное.

6.Максимаксный критерий – подход азартного игрока, самый оптимистичный критерий. При этом максимизируется максимум доходов и игнорируются возможные потери. Применение данного критерия часто ограничено из-за повышенного риска (особенно при принятия финансовых решений).

7. Критерий Гурвица является комбинированным, учитывающим как оптимистический, так и пессимистический подходы. При использовании этого критерия состояние природы берется не самым худшим и не самым лучшим, а некоторым промежуточным. При этом за оптимальную принимается стратегия, при которой

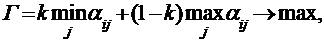(3.8)

где k – коэффициент, характеризующий долю пессимизма и оптимизма (изменяется от 0 до 1).

Коэффициент k выбирается по объективным соображениям (часто экспертно). При этом чем сложнее ситуация и необходимо застраховаться, тем ближе kк единице. При k=1 критерий Гурвица преобразуется в критерий Вальда.

Если рассматривать область применения вышеназванных критериев, то критерии Вальда и Сэвиджа используют при принятии разовых и ответственных решений, а Гурвица, Лапласа и Байеса - при менее ответственных, когда ситуация повторяется многократно (например, в оперативном планировании).

Поясним использование различных критериев принятия решения в условиях неопределенности внешней среды на примере.

Ситуация. Компания работает в условиях совершенной конкуренции. В будущем периоде невозможно однозначно определить, на каком уровне установится цена на производимый фирмой товар. Эксперты дают следующий прогноз цен: 14 руб./ед. с вероятностью 0,2; 15,5 руб./ед. с вероятностью 0,4; 18 руб./ед. – 0,4. Полные затраты компании можно описать следующей функциональной зависимостью:

З = 117,0 + 10Q + 0,0028Q²

Необходимо определить оптимальный объем производства для компании по данным платежной матрицы.

Решение. В соответствии с теорией предельной полезности оптимальный объем производства достигается, если предельные издержки равны предельному доходу, то есть прирост затрат при выпуске дополнительной единицы товара будет равен его цене. Таким образом, для каждого вероятностного уровня цены (14; 15,5 и 18 руб./ед.) необходимо найти оптимальный объем. Так как затраты представлены функциональной зависимостью, то прирост затрат будет определяться производной соответствующей функции

З’ = 10 + 0,0056Q .

Пример расчета показателей платежной матрицы:

П₁₁ = В₁₁(714) – З₁₁(714),

где П₁₁ – прибыль, получаемая компанией при объеме производства 714 ед. и цене на рынке 14 руб. за ед.;

В₁₁(714) – выручка компании при объеме производства 714 ед. и цене 14 руб. (В₁₁(714) = 14 * 714 = 9996 руб.);

З₁₁(714) – затраты при производстве 714 ед. товара (З₁₁(714) = 117 + 10*714 + 0,0028*(714)² = 8684,5 руб.);

П₁₁ = 9996 – 8684,5 = 1311,5 руб.

Аналогично рассчитываются остальные показатели платежной матрицы (табл. 2.1).

Приравнивая функцию производной к ценам, находим оптимальные объемы для каждой:

для цены 14 руб./ед. – 714 (ед.);

(10 + 0,0056Q = 14)

(Q_опт = 714)

для цены 15,5 руб./ед. – 982 (ед.);

для цены 18 руб./ед. – 1428 (ед.).

Переходим к составлению платежной матрицы. В качестве стратегий будут выступать оптимальные объемы производства, а состоянием природы – различные уровни цен. В платежной матрице будем рассчитывать прибыль (табл. 3.2).

Таблица 3.2.

Платежная матрица решений

Цены Объем производства		15,5		min
	1311,5	2382,5	4167,5	1311,5
	1110,8	2583,8	5038,8	1110,8
	-114,7	2027,2	5597,2	-114,7
Вероятность	0,2	0,4	0,4

Как видно по платежной матрице, доминирующего решения нет, поэтому следует воспользоваться известными критериями для выбора наилучшего варианта.

По критерию Вальда

β = max_i min_j а_ij =1311,5.

Критерий Вальда указывает, что самым оптимальным является объем, равный 714 ед., так как он обеспечивает максимальный из всех возможных минимальных выигрышей (причем производство на уровне 1428 ед. принесет убыток в 114,7 руб.).

По критерию Лапласа

Л₁ = 1/3*(1311,5 + 2382,5 + 4167,5) = 2620,5

Л₂ = 1/3*(1110,8 + 2583,8 + 5038,8) = 4142,6

Л₃ = 1/3*(-114,7 + 2027,2 + 5597,2) = 2503,2

В соответствии с критерием Лапласа оптимален объем производства на уровне 982 ед., но при этом считается, что три указанных уровня цен являются равновозможными. Так как имеются сведения о вероятностях, то лучше при выборе объема производства ориентироваться на критерий математического ожидания

МО₁ = 1311,5*0,2 + 2382,5*0,4 + 4167,5*0,4 = 2882,3

МО₂ = 1110,8*0,2 + 2583,8*0,4 + 5038,8*0,4 = 3271,2

МО₃ = -114,7*0,2 + 2027,2*0,4 + 5597,2*0,4 = 3026,8

Если руководствоваться критерием математического ожидания, то оптимальным объемом будет являться 982 ед., и в данном случае ему следует отдать предпочтение, опираясь на знание о вероятностях установления рыночных цен на том или ином уровне.