Задачи по основным темам курса

Тема. Методы оценки уровня риска

Задачи 1-10.

Среди клиентов коммерческого банка имеется пять должников, утративших в силу ряда обстоятельств платежеспособность и более года не возвращающих взятые у банка краткосрочные ссуды. По каждому должнику рассчитан коэффициент текущей ликвидности (КТЛ), значения которого приведены в таблице.

Номер варианта	Номер задачи	Значения КТЛ
I		1,12; 1,23; 1,34; 1,45; 1,56
II		1,56; 1,67; 1,78; 1,89; 1,91
III		1,33; 1,44; 1,55; 1,66; 1,77
IY		1,25; 1,35; 1,45; 1,55; 1,65
V		1,31; 1,42; 1,53; 1,64; 1,75
VI		1,47; 1,58; 1,69; 1,71; 1,82
VII		1,61; 1,72; 1,83; 1,94; 1,96
VIII		1,51; 1,63; 1,78; 1,84; 1,95
IX		1,24; 1,37; 1,42; 1,58; 1,78
X		1,53; 1,67; 1,74; 1,86; 1,97

Платежеспособным предприятием, у которого не возникает проблем с погашением долгов, принято считать такое, у которого КТЛ находится на уровне не ниже двух.

Используя лемму Маркова, найдите вероятности того, что должники не смогут довести КТЛ до двух и, очевидно, не вернут свои долги банку.

Задачи 11-20.

Коммерческий банк ведет статистику просрочки и невозврата ссуд, согласно которой достаточная гарантия платежеспособности имеется только у тех клиентов, где КТЛ оказывается на уровне не менее 3,5.

Это объясняется тем, что банк ведет дела с клиентами, активы которых не всегда бывают достаточно высокого качества. Активы этих клиентов не всегда можно быстро и без потерь продать, чтобы погасить за вырученные от этой продажи средства долги. Поэтому нормативное двукратное превышение активов над долгами в данном случае оказывается недостаточным.

Скорректируйте с учетом вышесказанного вероятности потерь банка на операциях с клиентами (использовать условие задач 1-10).

Задачи 21-30.

Среди дебиторов фирмы «Дон» имеется должник с большой просрочкой платежа по своему долгу. Эксперты фирмы смогли получить о финансовом положении этого должника, а именно о значениях коэффициента текущей ликвидности (КТЛ) за последние три месяца, приведенных в таблице.

Номер варианта	Номер задачи	Значения КТЛ
I		Месяцы КТЛ	1,6	1,7	1,5
II		Месяцы КТЛ	1,3	1,5	1,8
III		Месяцы КТЛ	1,2	1,4	1,7
IV		Месяцы КТЛ	1,5	1,4	1,2
V		Месяцы КТЛ	1,3	1,7	1,8
VI		Месяцы КТЛ	1,5	1,3	1,9
VII		Месяцы КТЛ	1,9	1,4	1,6
VIII		Месяцы КТЛ	1,8	1,9	1,5
IX		Месяцы КТЛ	1,7	1,4	1,6
X		Месяцы КТЛ	1,9	1,6	1,4

Определите вероятность того, что:

1) упомянутый должник сможет восстановить свою платежеспособность, подняв КТЛ до уровня не менее двух;

2) данный долг придется все-таки списать как безнадежный.

Используйте для ответа лемму Маркова и неравенство Чебышева, сопоставьте полученные с их помощью результаты и сделайте выводы.

Задачи 31-35.

На основании собранных статистических данных было установлено, что у предприятий, имеющих устойчивую платежеспособность, КТЛ находится на уровне не ниже b. У всех обанкротившихся предприятий КТЛ был зафиксирован на уровне не выше a. Используя модель равномерного распределения вероятностей, оцените вероятности утраты платежеспособности для предприятия с КТЛ на уровне x.

Номер	Номер	Значения
варианта	задачи	a	b	x
I		1,0	2,1	1,5
II		1,3	2,5	1,8
III		1,2	1,9	1,6
IV		1,0	2,0	1,7
V		1,4	2,3	2,0

Задачи 36-40.

Фирма собирается купить партию товара, цена которого обычно не выходит за пределы 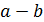(у.е.). Определите вероятность того, фирме удастся закупить товар по цене не дороже 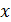(у.е.).

Номер	Номер	Значения
варианта	задачи	a	b	x
VI
VII
VIII
IX
X

Задача 41.

На основании следующей группировки предприятий и с помощью модели равномерного распределения определите для предприятия с уровнем коэффициента текущей ликвидности (КТЛ) 1,5:

1) границы зоны неопределенности;

2) вероятность наступления неплатежеспособности.

Исходные данные представлены в таблице.

Величина КТЛ	2,1	2,0	1,9	1,8	1,7	1,6	1,5	1,4	1,3	1,2	1,1
Предприятия с устойчивой платежеспособностью
Предприятия, утратившие платежеспособность

Задача 42.

На основании следующей группировки предприятий и с помощью модели равномерного распределения определите для предприятия с уровнем коэффициента текущей ликвидности (КТЛ) 1,4:

1) границы зоны неопределенности;

2) вероятность наступления неплатежеспособности.

Исходные данные представлены в таблице.

Величина КТЛ	2,1	2,0	1,9	1,8	1,7	1,6	1,5	1,4	1,3	1,2	1,1
Предприятия с устойчивой платежеспособностью
Предприятия, утратившие платежеспособность

Задача 43.

На основании следующей группировки предприятий и с помощью модели равномерного распределения определите для предприятия с уровнем коэффициента текущей ликвидности (КТЛ) 1,6:

1) границы зоны неопределенности;

2) вероятность наступления неплатежеспособности.

Исходные данные представлены в таблице.

Величина КТЛ	2,1	2,0	1,9	1,8	1,7	1,6	1,5	1,4	1,3	1,2	1,1
Предприятия с устойчивой платежеспособностью
Предприятия, утратившие платежеспособность

Задача 44.

На основании следующей группировки предприятий и с помощью модели равномерного распределения определите для предприятия с уровнем коэффициента текущей ликвидности (КТЛ) 1,7:

1) границы зоны неопределенности;

2) вероятность наступления неплатежеспособности.

Исходные данные представлены в таблице.

Величина КТЛ	2,1	2,0	1,9	1,8	1,7	1,6	1,5	1,4	1,3	1,2	1,1
Предприятия с устойчивой платежеспособностью
Предприятия, утратившие платежеспособность

Задача 45.

На основании следующей группировки предприятий и с помощью модели равномерного распределения определите для предприятия с уровнем коэффициента текущей ликвидности (КТЛ) 1,8:

1) границы зоны неопределенности;

2) вероятность наступления неплатежеспособности.

Исходные данные представлены в таблице.

Величина КТЛ	2,1	2,0	1,9	1,8	1,7	1,6	1,5	1,4	1,3	1,2	1,1
Предприятия с устойчивой платежеспособностью
Предприятия, утратившие платежеспособность

Задача 46.

Вкладчик хранит свои средства в двух банках: А и В. Согласно опубликованному рейтингу банков, надежность первого составила 87%, а второго – 91%. Определите вероятность того, что средства вкладчика:

а) полностью сохранятся;

б) будут полностью потеряны;

в) сохранятся только частично;

г) сохранятся хотя бы частично;

д) будут хотя бы частично потеряны.

Задача 47.

Временно свободные средства вложены равными долями в акции двух компаний. Надежность каждой из компаний инвестор оценивает на уровне 80%. Найдите вероятность того, что инвестированные средства:

а) полностью сохранятся;

б) сохранятся только частично;

в) сохранятся хотя бы частично;

г) будут полностью потеряны из-за банкротства эмитентов акций.

Задача 48.

Временно свободные средства фирма вложила в покупку акций двух компаний: «Нептун» и «Везувий». Надежность первой оценена экспертами в 95%, а второй – 70%. Определите:

а) вероятность того, что средства, инвестированные в покупку акций двух компаний, будут полностью потеряны из-за краха обеих компаний;

б) верно ли, что вероятность потери всех средств меньше, если их вложить только в одну, самую надежную компанию, и не иметь дел со второй, не очень надежной компанией;

в) вероятность частичной потери средств из-за краха какой-либо одной компании (безразлично какой);

г) вероятность того, что средства полностью сохранятся;

д) как проверить правильность расчетов по трем предыдущим пунктам;

е) есть ли необходимость диверсификации, и в чем она выражается.

Задача 49.

Эксперты определили надежность банка А на уровне 95% и банка В – на уровне 70%. Определите вероятность того, что:

а) оба банка обанкротятся;

б) оба банка не обанкротятся;

в) обанкротится только один (любой) банк;

г) обанкротится только банк А.

Задача 50.

Вероятность банкротства для фирмы в течение ближайшего года определена экспертами на уровне 0,22. Найдите вероятность банкротства в течение:

а) ближайшего полугодия;

б) ближайшего квартала;

в) ближайшего месяца;

г) ближайших двух лет;

д) ближайших трех лет.