Раздел 1. ЛОГИКА ФИНАНСОВЫХ РАСЧЕТОВ

ВВЕДЕНИЕ

В коммерческих вузах и училищах в дореволюционной России курс Финансовая математика преподавали под названием Высшие финансовые вычисления. В условиях административно-командной экономики, эта научная дисциплина в значительной степени утратила актуальность. Однако со становлением рыночных отношений вновь появилась потребность в использовании количественных методов оценки финансовых операций.

Практическая необходимость в применении методов финансовой математикиобусловлена переходом к экономическим методам управления, функционированием новых коммерческих структур, становлением рынка ценных бумаг, развитием банковского сектора, коренными изменениями условий проведения хозяйственных операций и т.д. В этих условиях управленческие решения нецелесообразно принимать лишь на интуитивной основе. Гораздо более качественные результаты могут быть достигнуты с помощью формализованных методов оценки, основанных на применении финансовой математики.

В настоящее время Финансовая математика является одним из наиболее динамично развивающихся разделов экономической науки, направленных на оптимизацию принимаемых решений при проведении финансовых и коммерческих операций. Любая такая операция предполагает согласование ее участниками целого ряда условий (параметров сделки): сумму кредита (займа, инвестиций), сроки, способы начисления процентов и погашения долга и т.д. При этом на результат финансовой операции в каждом случае оказывает влияние множество факторов, определяющих конъюнктуру финансового рынка. Без проведения количественного анализа затруднительно, а иногда и невозможно определить доходность той или иной финансовой операции и параметры финансовой сделки. Для решения этих и других задач служат методы финансовой математики.

В пособии изложены следующие разделы:

1) логика финансовых вычислений;

2) вычисления по простым процентам;

3) вычисления по сложным процентам;

4) финансовая эквивалентность обязательств;

5) оценка эффективности финансовых операций;

6) финансовые ренты;

7) кредитные расчеты;

8) финансовые расчеты в инвестиционном анализе;

9) инвестиционный анализ на рынке ценных бумаг;

10) экономические расчеты при проведении валютных операций;

11) финансовые расчеты в страховании.

Курс лекций предназначен для студентов специальности Финансы и кредит, студентов других экономических специальностей, преподавателей финансово-экономических дисциплин, а также специалистов в области экономики и финансов.

Раздел 1. ЛОГИКА ФИНАНСОВЫХ РАСЧЕТОВ

Предмет и метод курса «Финансовая математика»

Финансовая математика – это наука, изучающая методы и методики определения стоимостных и временных параметров финансовых и инвестиционных операций, процессов и сделок, а также модели управления инвестициями, капиталом и его составляющими.

Объект финансовой математики – финансовые операции и сделки и их технико-экономическое обоснование, направленное на извлечение прибыли. Предмет – финансовые и актуарные оценки показателей эффективности этих операций и сделок, а также доходов отдельно взятых участников этих сделок, определяемых в виде процентных ставок, норм и коэффициентов, скидок, доходов и дивидендов, ренты и маржи, котировок ценных бумаг, курсов валют, курсовых разниц и пр.

В курсе финансовой математики систематически излагаются методы количественного анализа, используемые при принятии управленческих решений в финансовой сфере. Рассматриваются методы учета факторов времени, инфляции, оценки потоков платежей, операций с ценными бумагами и др.

Финансовая математика охватывает определенный круг методов вычислений, необходимость в которых возникает всякий раз, когда в условиях сделки или финансово-банковской операции оговариваются конкретные значения трех видов параметров:

1) стоимостные характеристики (размеры платежей, долговых обязательств, кредитов и т. д.);

2) временные данные (даты и сроки выплат, продолжительность льготных периодов, отсрочки платежей и т. д.);

3) процентные ставки (последние иногда задаются в открытой форме).

Применение методов финансовой математики

В практической работе

Методы финансовой математики используются в расчетах параметров, характеристик и свойств инвестиционных операций и стратегий, параметров государственных и негосударственных займов, ссуд, кредитов, в расчетах амортизации, страховых взносов и премий, пенсионных начислений и выплат, при составлении планов погашения долга, оценке прибыльности финансовых сделок.

Методы финансовой математики чаще всего применяются при решении следующих практических задач:

1) исчисление конечных сумм денежных средств, находящихся во вкладах, займах, ценных бумагах путем начисления процентов;

2) учет ценных бумаг;

3) установление взаимосвязи между отдельными параметрами сделки и определение параметров сделки, исходя из заданных условий:

4) определение эквивалентности параметров сделки для получения равной отдачи от затрат, произведенных различными способами;

5) анализ последствий изменения условий финансовой операции;

6) исчисление обобщающих характеристик и отдельных параметров денежных средств, рассматриваемых как финансовые потоки;

7) разработка планов выполнения финансовых операций;

8) расчет показателей доходности финансовых операций и др.

На практике методы финансовой математики применяют в работе финансовых организаций, торговых фирм и инвестиционных компаний, фондовых и валютных бирж.

Виды процентов

Методы финансово-экономических расчетов различны в зависимости от вида применяемых процентов. Относительно момента выплаты или начисления дохода за пользование предоставленными денежными средствами проценты подразделяются на обычные (декурсивные) и авансовые (антисипативные).

Отрезок времени между двумя следующими друг за другом процедурами начисления процентов или срок финансовой операции, если проценты начисляются один раз, называется периодом начисления процентов.

Обычные проценты начисляются в конце периода относительно исходной величины средств. Доход, определяемый обычным процентом, выплачивается в конце периодов финансовой операции. Такие проценты применяют в большинстве депозитных и кредитных операций, а также в страховании.

Авансовые (антисипативные) проценты начисляются в начале периода относительно конечной суммы денег. Доход, определяемый авансовым процентом, выплачивается в момент предоставления кредита. Такая форма расчетов называется авансовой или учетом. При этом базой расчета процентов служит сумма денег с процентами (сумма погашения долга). Исчисленные таким образом проценты взимаются вперед и являются авансом. Так рассчитывают проценты в некоторых видах кредитования, операциях с дисконтными ценными бумагами, в международных расчетах.

Рассмотренным двум видам процентов на практике соответствуют определенные процентные ставки. Это, во-первых, обычная ставка процентов - rote of interest ( 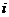) которая рассчитывается как отношение дохода, полученного за определенный период времени к величине капитала, предоставляемого в кредит. Во-вторых, учетная (антисипативная) ставка - discount rote ( ). Учетная ставка рассчитывается, как отношение дохода, полученного за определенный период времени к ожидаемой сумме погашения долга.

Простейшим видом финансовой операции является однократное предоставление в долг некоторой суммы с условием, что через n лет будет возвращена большая сумма . В этом случае обычная годовая ставка процентов рассчитывается по формуле (1), а учетная ставка — по формуле (2):

(1.1)

(1.2)

В экономической литературе первый показатель также называют «процентная ставка», «процент», «рост», «ставка процента», «норма прибыли», «доходность», а второй - «учетная ставка», «дисконт». Обе ставки взаимосвязаны, т.е. зная один из показателей, можно рассчитать другой по формулам (3) и (4) соответственно:

(1.3)

(1.4)

В зависимости от условий проведения финансовых операций, начисление процентов может осуществляться с применением простых, либо сложных процентов.

Простые проценты, как правило, используются в краткосрочных финансовых операциях, срок проведения которых меньше года. Базой для исчисления процентов за каждый период в этом случае служит первоначальная (исходная) сумма сделки.

Сложные проценты широко применяются в долгосрочных финансовых операциях со сроком проведения более одного года. Однако могут быть использованы и в краткосрочных финансовых операциях, если это предусмотрено условиями сделки. При этом база для начисления процентов меняется за счет присоединения ранее начисленных процентов, т.е. она включает в себя как исходную сумму сделки, так и сумму уже накопленных к этому времени процентов.

Практика расчетов процентов основывается на теории наращения денежных средств по арифметической или геометрической прогрессии. Арифметическая прогрессия соответствуют простым процентам, геометрическая - сложным.

Пример.Предприниматель получил на два года кредит в размере 100 тыс. руб. В конце срока он должен возвратить 140 тыс. руб. Определите годовые процентную и учетную ставки.

Решение:

Наращение и дисконтирование

Процесс, в котором по заданной исходной сумме и процентной ставке необходимо найти ожидаемую в будущем к получению сумму, в финансовых вычислениях называется процессом наращения. Процесс, в котором по заданной ожидаемой в будущем к получению сумме и процентной ставке необходимо найти исходную сумму долга называется процессом дисконтирования. Логика финансовых операций схематически изображена на рис. 1.

Рис. 1. Логическая схема операций наращения и дисконтирования.

Экономический смысл метода наращения состоит в определении величины, которая будет или может быть получена из некоторой первоначальной (текущей) суммы в результате проведения операции. Другими словами, метод наращения позволяет определить будущую величину (future value - 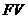) текущей суммы (present value - 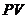) через некоторый промежуток времени, исходя из заданной процентной ставки.

Дисконтирование представляет собой процесс нахождения современной на заданный момент времени суммы по ее известному или предполагаемому значению в будущем, исходя из заданной процентной ставки.

В экономическом смысле величина 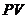, найденная в процессе дисконтирования, показывает современное (с позиции текущего момента времени) значение будущей величины 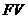. Таким образом – дисконтирование – это по сути дела зеркальное отражение наращения. Используемую при этом процентную ставку называют нормой дисконта.

Реинвестирование

Если по прошествии некоторого периода зафиксированная к данному моменту наращенная сумма инвестируется вновь, то такая операция называется реинвестированием (повторным инвестированием) или капитализацией полученных на каждом этапе наращения средств. В этом случае проценты начисляют на уже наращенные в предыдущем периоде суммы, т.е. происходит многоразовое наращение.

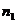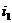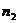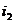Предположим, что в течение периода времени установлена ставка простых процентов , тогда к концу этого периода наращенная сумма составит . Затем эта сумма будет помещена наследующий срок под простых процентов. К концу периода 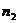наращенная сумма будет равна величине и т.д.

Таким образом, итоговая наращенная сумма определится по формуле:

(2.4.)

где — продолжительность периодов наращения;

- процентные ставки, по которым производится реинвестирование.

Пример. Клиент поместил в банк 500,0 тыс. руб. Какова будет наращенная за 3 месяца сумма вклада, если за первый месяц начисляются проценты в размере 10% годовых, а каждый последующий месяц процентная ставка возрастает на 5% с одновременной капитализацией процентного дохода?

Решение:

Пример.

Имеются два кредитных обязательства 400 тыс. руб. и 700 тыс. руб. со сроками уплаты 1 августа и 1 января (следующего года). По согласованию сторон условия обязательств пересмотрены: первый платеж в размере 600 тыс. рублей должник вносит 1 ноября, остальной долг он выплачивает 1 марта. Определите величину второго платежа, если в расчетах используется простая процентная ставка 20% годовых. Проценты точные.

Решение:

За базовую дату примем дату искомого платежа. Все остальные платежи приведем к этой дате - 1 марта.

Срок от 1 августа (Р1=400 тыс. рублей) до 1 марта составляет 212 дней (365-213 +60).

Срок от 1 января (Р2=700 тыс. рублей) до 1 марта составляет 59 дней (60-1).

Срок от 1 ноября (Р3=600 тыс. рублей) до 1 марта составляет 120 дней (365-305+60).

Уравнение эквивалентности имеет вид:

Отсюда Р4=529,65 тыс. рублей.

Пример.

Согласно контракту предприятие должно выплатить 200, 300 и 500 тыс. рублей соответственно через 1,5 года, 2 и 4 года. Предприятие предлагает пересмотреть контракт и вернуть долг одним платежом через 3,5 года. Найдите величину консолидированного платежа, если применяется сложная процентная ставка 18% годовых.

Решение:

Пример

Ссуда в размере 2,5 млн. рублей выдана под простые проценты на 2 года, с условием возвратить в конце срока 3,5 млн. руб. Определить доходность этой операции на основе простой и сложной процентных ставок.

Решение: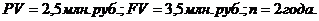

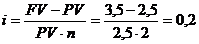или 20%.

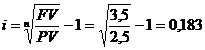или 18,3%.

Пример

На вклад, помещенный в банк под 16% годовых, проценты начисляются ежеквартально. Оцените доходность этой операции на основе эффективной процентной ставки.

Решение: i=0,16; m=4.

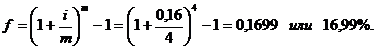
В некоторых финансовых операциях общий доход может исчисляться как результат сложения доходов от разных источников. Так, банки кроме взимания процентной ставки за кредит часто устанавливают комиссионное вознаграждение за осуществление операций по расчетным счетам клиентов а также удерживают с клиента определенную сумму, покрывающую затраты банка по каждой операции.

Следовательно, измерение доходности любой финансовой операции сводится к учету всех источников дохода, нахождению суммарного дохода за определенный период времени и сопоставлению его с затратами. Для кредитных операций – это сумма денег, предоставленная в кредит. Для владельца ценных бумаг – это сумма, затраченная для их приобретения. При этом все выплаты должны быть приведены к одному моменту времени, чаще всего к сроку начала или окончания финансовой операции.

Таким образом, в общем случае оценка доходности сводится к определению расчетной процентной ставки, отражающей общую доходность на вложенный капитал.

Пример

Ссуда 100 тыс. рублей выдана на 240 дней под 12% годовых. Проценты простые обыкновенные. При выдаче ссуды удержаны комиссионные в размере 1тыс. рублей. Определить полную доходность финансовой операции в виде сложной процентной ставки.

Решение: PV=100 тыс. руб.; t = 240 дней; Y = 360 дней.

Сумма долга с процентами составит:

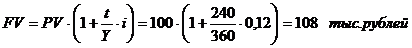
Затраты составили 99 тыс. руб. (100-1). Срок финансовой операции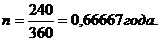

Определим полную доходность финансовой операции в виде сложной процентной ставки из равенства: .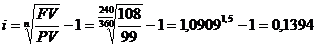

Следовательно, полная доходность этой финансовой операции составляет 13,94%.

Раздел 6. ФИНАНСОВЫЕ РЕНТЫ

Потоки платежей

Современные финансово-банковские операции часто предполагают не отдельные или разовые платежи, некоторую их последовательность во времени. Например, погашение задолженности в рассрочку, выплата дивидендов, пенсий и т.д.

Ряд следующих друг за другом выплат и поступлений называют потоками финансовых платежей. Финансовые потоки могут быть регулярными и нерегулярными.

В регулярных финансовых потоках поступление средств осуществляется через одинаковые промежутки времени, например, взносы от погашения кредита, перечисление прибыли и т.п.

Регулярные финансовые потоки называют также финансовыми рентами или аннуитетами. Величину каждой отдельной выплаты денег, входящей в состав ренты, называют членом ренты. Рентные платежи производят через равные промежутки времени. Эти временные интервалы между двумя платежами называют периодом ренты. Время, измеренное от начала финансовой ренты до конца последнего ее периода называется сроком ренты. Процентная ставка представляет собой ставку, используемую при наращении или дисконтировании платежей, из которых состоит рента. Наряду с этим, при характеристике отдельных видов финансовых рент применяются параметры: число платежей в году, число начисления процентов, моменты произведения платежей и др.

Виды финансовых рент

В зависимости от размера платежа различают ренты постоянные и переменные. По времени осуществления платежи могут производиться в начале процентного периода. Такая рента называется пренумерандо. Если платежи осуществляются в конце процентного периода, то рента называется постнумерандо. Исходя из продолжительности периода, существуют годовые, полугодовые, ежемесячные, р-срочные, платежи. Регулярные финансовые потоки могут быть безусловными и условными. Последние выплачиваются после поступления какого-либо события. Различают также ренты немедленные, действие которых начинается сразу после заключенного договора, и отложенные, платежи по которым производятся по истечении некоторого оговоренного периода.

M раз в год

Рассмотрим случай, капитализация процентов осуществляется чаще, чем один раз в год.

Предположим, проценты начисляются m раз в год. В этом случае их каждый раз начисляют по ставке , где i - номинальная ставка процентов. Срок ренты n лет.

Наращенные платежи представляют собой геометрическую прогрессию с первым членом R и знаменателем прогрессии .

Наращенная сумма такой ренты определяется по формуле:

(6.3)

где R- размер годового платежа.

Пример. На банковский счет ежегодно в конце года поступает 10 000 рублей в течение 7 лет. На эти средства ежеквартально начисляют проценты по номинальной ставке 15% годовых. Определить, какая сумма будет на банковском счете к концу срока.

Решение: R=10 000 руб.; m = 4 раза в год; n =7 лет; i = 0, 15.

Вечные ренты

Наращенная сумма вечной ренты при любых ее параметрах равна бесконечно большой величине, в то же время ее современная величина имеет конкретное значение. Современная величина вечной ренты оказывается полезной характеристикой в ряде финансовых расчетов, например при замене некоторых потоков платежей, оценке финансовых инвестиций, в страховых расчетах.

Современная величина вечной годовой ренты определяется по формуле: (6.10)

Пример. Квартира арендована за 10000 $ в год. Какова выкупная цена аренды при годовой ставке процента 5%?

Решение: R = 10 000 $; i = 0,05.

Выкупная цена ренты - это современная величина всех будущих арендных платежей. Она равна .

Заметим, что если поместить 200000 $ в банк под 5% годовую ставку, то годовые процентные деньги составят в точности 10 000 $.

Формула для вычисления современной стоимости р-срочной вечной ренты с начислением процентов m раз в году имеет вид:

(6.11)

Пример. Определите цену вечной ренты, выплаты по которой в конце каждого месяца составляют 2 тыс. рублей при номинальной процентной ставке 12% годовых и ежеквартальном начислении процентов.

Решение:

Конверсия рент

В ряде случаев возникает необходимость принять условия финансового соглашения, предусматривающего выплату ренты. Процесс, связанный с изменением условий ренты, называется конверсией ренты. Иногда конверсия ренты заключается в замене ренты единовременным платежом. Иногда рента с одним набором условий заменяется рентой с другими условиями. При этом предполагается, что конверсия рент не приводит к изменению финансовых последствий для каждого из участвующих в соглашении сторон, то есть она должна основываться на принципе финансовой эквивалентности платежей.

При этом находят современную величину данной ренты, а затем подбирают ренту с такой же современной величиной и нужными параметрами.

Пример. Годовую ренту пренумерандо со сроком 5 лет, разовым платежом 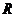=2000 руб. и процентной ставкой 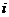=6% необходимо заменить рентой сроком 8 лет. Определите параметры ренты.

Решение: R1=2 000 руб.; i=0,06; n1=5;n2=8.

1).Определим современную стоимость такой ренты.

2). Найдем разовый платеж восьмилетней ренты с такой же современной стоимостью. Для этого составим уравнение эквивалентности:

3). Разрешим это уравнение относительно

Объединение рент

Предположим, несколько рент необходимо заменить одной. Замена базируется на принципе финансовой эквивалентности обязательств, который реализуется путем составления уравнения эквивалентности.

При составлении уравнения эквивалентности находят современные величины рент-слагаемых и суммируют, а затем приравнивают эту сумму современной стоимости заменяющей ренты.

Правило объединения рент:

1) находят современные величины рент-слагаемых и суммируют их;

2) приравнивают полученную сумму современной стоимости заменяющей ренты;

3) задав все параметры заменяющей ренты, кроме одного, из уравнения эквивалентности определяют недостающий параметр.

Пример.

Найти ренту-сумму для двух годовых рент постнумерандо: одна -длительностью 5 лет с годовым платежом 1000 $. , а другая - 8 лет с годовым платежом 800 $. Годовая ставка процента равна 8%.

Решение:

- современная величина первой ренты.

- современная величина второй ренты.

3) Определим современную величину ренты-суммы:

3992,7+4597,28=8590,02=8589,98 $.

Теперь можно задать либо длительность ренты-суммы, либо годовой платеж и затем определить второй из этих параметров.

Предположим, что рента – сумма имеет длительность 6 лет, тогда уравнение эквивалентности имеет вид:

Отсюда: .

Переменные финансовые ренты

Наряду с постоянными рентами, в последние годы, в финансовой практике часто встречаются ренты, параметры которых изменяются во времени. Такие ренты носят называние переменных во времени.

Суть расчета в этом случае сводится к тому, что, если процесс изменения переменной ренты носит не систематический характер, и соответственно его нельзя описать аналитически, то величину будущей и современной стоимостей таких потоков следует определять прямым счетом, наращивая и дисконтируя к требуемому моменту времени отдельные платежи и затем суммируя полученные величины.

В общем случае современную стоимость финансовой ренты постнумерандо можно представить таким образом:

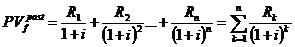(6.12)

Здесь 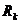ожидаемые поступления в момент времени 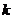; 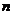- временной горизонт.

Расчет современной стоимости регулярных финансовых потоков используют при выборе наилучшего варианта инвестирования и возврата долга.

Пример. Имеется переменный финансовый поток постнумерандо 20,12,8,45,30 (тыс. руб.). Рассчитайте приведенную стоимость финансового потока, если его период совпадает с базовым периодом начисления процентов по сложной процентной ставке 25% годовых, т.е. равен одному году. Как изменяется оценка финансового потока, если он представляет собой поток пренумерандо?

Решение: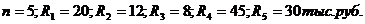

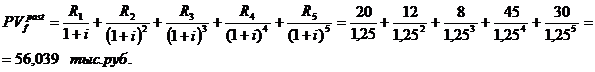
Для определения стоимости финансового потока пренумерандо необходимо умножить полученный результат на .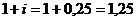

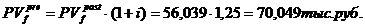
Раздел 7. КРЕДИТНЫЕ РАСЧЕТЫ

Планирование погашения задолженности

Одним из практических приложений финансовой математики является разработка плана погашения средне- и долгосрочных кредитов.

К среднесрочным, как правило, относят кредиты, выданные на срок от 2 до 5 лет. Кредиты, выданные на более длительный срок, являются долгосрочными.

Расходы, связанные с погашением займа, должны включать как текущие выплаты процентов, так и средства, предназначенные для погашения суммы займа, или основного долга. В совокупности они называются расходами заемщика по обслуживанию долга или амортизацией займа.

Существуют различные способы погашения задолженности. Участники кредитной сделки оговаривают их при заключении контракта. В соответствии с условиями контракта составляется план погашения задолженности. Одним из важнейших элементов плана является определение количества выплат в течение года, т.е. определение числа так называемых срочных уплат и их величины.

Срочные уплаты рассматриваются как средства, предназначение для погашения, как основного долга, так и текущих процентных платежей. При этом средства, направляемые на погашение (амортизацию) основного долга, могут быть равными или изменяющимися, а плата за кредит, вычисленная по сложным процентам, может выплачиваться отдельно. Иногда в течение ряда лет выплачиваются только проценты за кредит, а сам долг погашается в оставшееся время в рассрочку, т.е. несколькими платежами, или разовым платежом.

Погашение кредита может также производиться в виде финансовой ренты, т.е. платежами, вносимыми через равные промежутки времени и содержащими как выплату основного долга, так и процентный платеж за пользование кредитом. Величина срочных уплат зависит от величины кредита, его срока, наличия и продолжительности льготного периода, размера процентной ставки и т.п. Однако, как правило, проценты за кредит должны выплачиваться и в льготном периоде. Рассмотрим некоторые методы разработки планов погашения кредитов.

Равными выплатами

Потребительный кредит предоставляется для покупки предметов личного потребления. Существуют различные формы потребительского кредита, отличающиеся друг от друга методами и сроками его погашения. Так, например, кредит может быть предоставлен с отсрочкой платежа и последующим разовым погашением всей суммы. Другой метод предусматривает погашение платежа в рассрочку, частями.

Если кредит, выданный потребителю, будет погашен равными выплатами, то наращенная сумма долга будет определяться по формуле: . Сумму разового погасительного платежа, если платеж осуществляется m раз в году, можно определить по формуле: .

Пример. Холодильник ценой 8 тыс. руб. продается в кредит на два года под 10 % годовых. Погасительные платежи вносятся ежемесячно. Определить размер разового платежа.

Решение:

Сумма, подлежащая погашению за весь срок кредита:

Разовый платеж:

Основные понятия инвестиционного анализа

Латинское слово invest означает «вкладывать». Вложение денежных средств и других капиталов в реализацию различных экономических проектов или в ценные бумаги с целью получения прибыли, называется инвестированием, а сами вкладываемые средства инвестициями. Целью инвестирования является получение прибыли, увеличение капиталов.

Важнейшими задачами анализа инвестиционных проектов является определение их финансовой эффективности и сравнение эффективности альтернативных инвестиционных проектов с целью выбора наилучшего из возможных вариантов инвестирования.

Инвестиционные проекты являются альтернативными, если реализация одного из них исключает возможность реализации другого. Например, частный инвестор приобретает акции компании «Норильский никель» на сумму 2,5 млн. рублей. В этом случае эти деньги уже не могут быть положены на депозит в Сбербанк. Следовательно, эти варианты инвестирования денежных средств являются альтернативными. Для выбора наилучшего варианта инвестирования необходимо провести инвестиционный анализ.

Один из ключевых моментов при принятии инвестиционных решений составляет оценка эффективности предполагаемых капиталовложений. Существующие методы оценки инвестиций можно разбить на две группы: статические или учетные и динамические, учитывающие фактор времени.

Динамические методы отражают наиболее современные подходы к оценке эффективности инвестиций. Они преобладают в практике крупных и средних предприятий развитых стран. Эти методы часто называют дисконтными, поскольку они базируются на определении современной величины денежных потоков, связанных с реализацией инвестиционного проекта.

НА РЫНКЕ ЦЕННЫХ БУМАГ

Оценка облигаций

По способам выплаты дохода различают облигации с фиксированной или плавающей купонной ставкой и облигации с нулевым купоном. Для облигации с нулевым купоном эмиссионный курс устанавливается ниже номинального. Разница между ценой приобретения облигации и ценой ее погашения представляет собой доход инвестора. Периодическая выплата процентов по купонным облигациям осуществляется по купонам — вырезным талонам с напечатанной на нем цифрой купонной ставки. Периодичность выплаты процента по облигации определяется условиями займа. Она может быть квартальной, полугодовой или годовой. При прочих равных условиях, чем чаще начисляется доход, тем облигация выгоднее, тем выше ее рыночная цена.

Облигации могут быть охарактеризованы различными стоимостными показателями, основными из которых являются нарицательная (или номинальная), а также выкупная и рыночная цены. Нарицательная стоимость напечатана на самой облигации и используется чаще всего в качестве базы для начисления процентов. Этот показатель имеет значение только в двух случаях: в момент выпуска облигации при установлении цены размещения, а также в моменты начисления процентов, если они привязаны к номиналу. В период размещения облигационного займа цена облигации, как правило, совпадает с ее нарицательной стоимостью.

Выкупная цена (синонимы: цена досрочного погашения, отзывная цена) — это цена, по которой производится выкуп облигации эмитентом по истечении срока облигационного займа или до этого момента, если такая возможность предусмотрена условиями займа. Эта цена совпадает с нарицательной стоимостью, как правило, в том случае, если заем не предполагает досрочного его погашения.

Рыночная (курсовая) цена облигации определяется конъюнктурой рынка. Значение рыночной цены облигации в процентах к номиналу ( ) называется курсом облигации. Как уже отмечалось выше, эта цена может не совпадать с текущей внутренней стоимостью облигации.

Курс облигации определяется из выражения

Пример. Облигация номиналом 500 руб. продается по
цене 465 руб., определите ее курс.

.

Оценка бессрочных облигаций

Бессрочная облигация предусматривает неопределенно долгую выплату дохода в установленном размере А. В этом случае имеем вечную ренту постнумерандо для любого 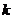), и формула принимает вид

Пример.Определить теоретическую стоимость бессрочной облигации, если выплачиваемый по ней годовой доход составляет 1 тыс. руб., а приемлемая норма прибыли — 16%.

Решение:

Теоретическая стоимость бессрочной облигации:

Таким образом, в условиях равновесного рынка в данный момент времени облигации такого типа будут продаваться по цене равной 6250 руб. По мере изменения рыночной нормы прибыли цена облигации может меняться.

Основные понятия валютных расчетов

В периоды экономической нестабильности, высокой инфляции многие граждане предпочитают хранить сбережения в свободно конвертируемой валюте (СКВ) или на валютных депозитах.

Валюта покупается и продается, как и любой другой товар, исходя из спроса и предложения. Конечная цена иностранной валюты, полученная в результате торгов, выражается в валютном курсе. Валютный курс – это цена денежной единицы национальной валюты, выраженная в денежных единицах другой страны. Установление курса иностранной валюты называется котировкой.

Различают прямую и косвенную котировку валюты. При прямой котиро<