Модели и задачи линейного и нелинейного программирования
В банковской деятельности
Ответственные решения в современных целенаправленных системах планирования и управления должны быть в некотором смысле экстремальными или близкими к ним. Отступление от этого принципа обычно связано с излишними затратами (часто весьма значительными) и снижает эффективность управления (часто весьма существенно).
При моделировании банковской деятельности часто приходится сталкиваться с задачей математического программирования, которая может быть сформулирована следующим образом: найти значения переменных 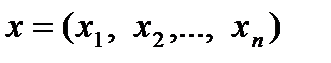 , которые удовлетворяют неравенствам
, которые удовлетворяют неравенствам
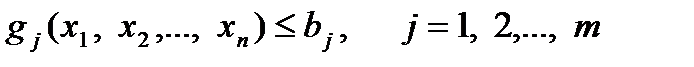 (2.3.1)
(2.3.1)
и обращают в минимум (максимум) функцию 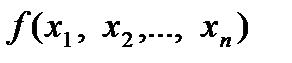 :
:
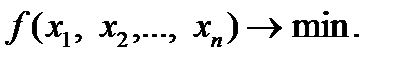 (2.3.2)
(2.3.2)
Вид функций 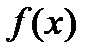 и
и 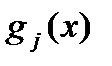 определяет класс задач математического программирования. Если все функции
определяет класс задач математического программирования. Если все функции 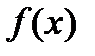 ,
, 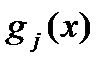 ,
, 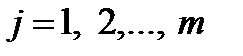 линейны, получаем задачу линейного программирования. Если хотя бы одна из функций нелинейна, имеем задачу нелинейного программирования.
линейны, получаем задачу линейного программирования. Если хотя бы одна из функций нелинейна, имеем задачу нелинейного программирования.
Классические методы поиска экстремума в задачах нелинейного программирования тесно связаны с понятием выпуклой функции, седловой точки, необходимыми и достаточными условиями экстремума (теорема Куна-Таккера), функцией и множителями Лагранжа
План, набор команд управления или проект часто могут быть формально представлены в виде системы чисел или функций, удовлетворяющих определенным ограничениям — равенствам, неравенствам или логическим соотношениям. План, система команд управления или проект оптимальны, если они, кроме того, обращают в минимум или в максимум (в зависимости от постановки задачи) некоторую функцию от искомых параметров — показатель качества решения.
Записи (2.3.1), (2.3.2), вполне осмысленные при детерминированных значениях параметров условий задачи, теряет определенность и требует дополнительных разъяснений при случайных значениях исходных данных. Между тем во многих прикладных задачах коэффициенты целевой функции, элементы функции условий или составляющие вектора ограничений — случайные величины.
Исходная информация для планирования, проектирования и управления в экономике, как правило, недостаточно достоверна. Планирование производства обычно ведется в условиях неполной информации об обстановке, в которой будет выполняться план и реализовываться произведенная продукция. Во всех случаях в моделях математического программирования, к исследованию которых сводятся задачи планирования, проектирования и управления, отдельные или все параметры целевой функции и ограничений могут оказаться неопределенными или случайными, Естественный на первый взгляд путь анализа подобных задач—замена случайных параметров их средними значениями и вычисление оптимальных планов полученных таким образом детерминированных моделей—не всегда оправдан. При сглаживании параметров условий задачи может быть нарушена адекватность модели изучаемому явлению. Усреднение исходных данных может привести к потере полезной информации и привнести в модель ложную информацию. Решение детерминированной задачи с усредненными параметрами может не удовлетворять ограничениям исходной модели при допустимых реализациях параметров условий.
