Стохастическое программирование

Оптимизационные задачи и их модели рассматривались в предыдущих параграфах в предположении, что вся исходная информация задана строго однозначно. Такие задачи и модели называют детерминированными. В действительности же детерминированные модели часто оказываются неадекватными реальным процессам в экономике. Это объясняется неполнотой, неточностью данных, на основе которых формируется модель. В одних случаях некоторые (а возможно, и все) параметры модели носят вероятностный характер. Тогда говорят о ситуациях, связанных с риском. В других случаях имеющаяся информация не позволяет составить представление о характере изменения параметров, описывающих изучаемый процесс. Такие ситуации называют неопределенными. Оптимизационные задачи, при постановке которых нет исчерпывающих данных об их условиях, называют стохастическими. Поскольку стохастические задачи приходится ставить и решать при недостаточной информации, это ведет к снижению экономической эффективности получаемых решений.

Для исследования описанных ситуаций разрабатываются специальные методы, объединяемые в разделе математического программирования, называемом стохастическим программированием. Стохастическое программирование изучает теорию и методы решения условных экстремальных задач при неполной информации об условиях задач.

Различают пассивное и активное стохастическое программирование. Пассивное стохастическое программирование – это совокупность приемов, позволяющих находить наилучшие решения и экстремальные значения целевых функций в оптимизационных задачах со случайными исходными данными. При этом используются в частности, идеи параметрического программирования. Активное стохастическое программирование – это совокупность приемов, позволяющих развивать методы выбора решений в условиях риска и неопределенности.

В стохастическом программировании исследуются одно-, двух- и многоэтапные задачи.

Одноэтапными называют задачи, в которых последовательность поступления исходной информации не имеет значения при выборе решения, оно принимается один раз и в дальнейшем не корректируется. Такие задачи могут порождаться детерминированными оптимизационными задачами, когда исходные данные теряют определенность и приобретают случайный характер. В одноэтапных задачах по-разному выбираются целевая функция и характер ограничений. В качестве целевой функции может рассматриваться вероятность попадания решения в некоторую, вообще говоря, случайную область или математическое ожидание некоторой функции от решения. В одних случаях ограничения задачи могут удовлетворяться при всех возможных значениях случайных параметров (жесткая постановка). В других случаях требуется, чтобы вероятность попадания решения в допустимую область была не меньше данного числа (модель с вероятностными ограничениями). В каждой конкретной задаче приходится специально оговаривать, что называть планом и оптимальным планом.

Естественный на первый взгляд путь замены случайных параметров их средними значениями и поиск оптимальных планов полученных таким образом детерминированных задач во всех случаях не всегда оправдан. При усреднении параметров условий задачи может быть нарушена адекватность модели изучаемому явлению. Оптимальный план детерминированной задачи с усредненными параметрами не всегда удовлетворяет условиям задачи при различных возможных комбинациях параметров ограничений. Этот прием применяют лишь для приближенного решения стохастической задачи.

На практике чаще других встречаются двухэтапные стохастические задачи. Подобные задачи возникают, например, при планировании выпуска продукции в случае, когда отсутствуют данные о спросе на нее. В такой ситуации сначала принимается предварительное решение об объеме выпуска на основе имеющейся информации (1-й этап), затем после установления спроса принимается корректирующее решение (2-й этап). При этом предварительное решение не должно исключать возможность его коррекции на втором этапе. Кроме того, предварительный и корректирующий планы согласовывают так, чтобы обеспечивались минимальные средние затраты за оба этапа. Для ряда конкретных постановок двухэтапных стохастических задач разработаны достаточно надежные методы решения.

В многоэтапных (динамических) задачах по мере получения информации о развивающемся процессе имеется возможность неоднократно корректировать решение, учитывая исходные ограничения и априорные статистические характеристики случайных параметров, описывающих процесс на каждом этапе. Многоэтапные задачи могут быть как с жесткими, так и с вероятностными ограничениями. Примерами многоэтапных стохастических задач являются задачи перспективного планирования, регулирования технологических процессов оперативного управления космическими объектами и др. Многоэтапные стохастические задачи представляют для практики наибольший интерес.

В качестве примера, рассмотрим задачу о наиболее рациональном управлении запасами продукта. На складе хранится запас некоторого продукта в течении 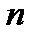периодов времени. На начало первого периода запас составляет 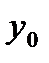единиц. Количество продукта, отправляемого со склада в 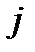-й период, определяется спросом 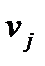на этот продукт. При этом спрос 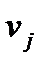в каждый данный период считается случайной величиной с плотностью вероятности 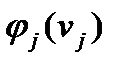. Предполагается, что для различных периодов эти случайные величины независимы. Стоимость доставки единицы заказанного продукта с предприятия на склад в 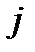-й период равна 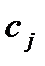(заказ делается в начале каждого периода, а доставка его на склад производится до конца этого же периода). Стоимость хранения единицы продукта в 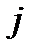-м периоде равна 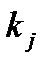, а стоимость хранения запаса пропорциональна его количеству 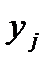в конце периода и составляет 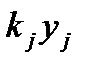. За отсутствие продукта на складе при наличии спроса на него в 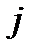-м периоде начисляется штраф, равный 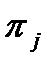в расчете на единицу продукта. Штраф увеличивается пропорционально количеству отказов 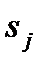к концу 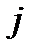-го периода и равняется .

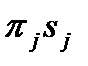Требуется так спланировать поступление продукта на склад, чтобы минимизировались суммарные расходы, связанные с его доставкой, хранением и штрафами за отсутствие продукта при наличии спроса.

Обозначим через 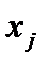количество единиц продукта, заказываемого на 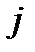-й период. Тогда к концу 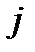-го периода запас продукта

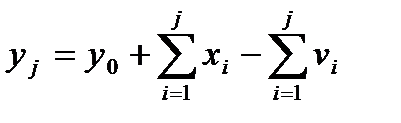(1.4.1)

Очевидно, что работа склада должна строиться таким образом, чтобы поддерживать 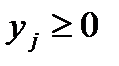. Однако это не всегда удается, и число отказов из-за отсутствия продукта на складе к концу -го периода оказывается равным

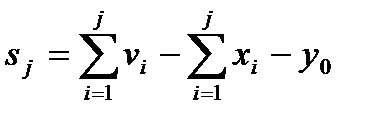
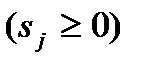. (1.4.2)

Наличие запаса и штрафа – взаимоисключающие моменты: если в течении какого-то 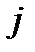-го периода 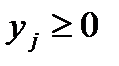то 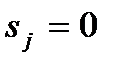, и наоборот, т. е. если приходится платить за хранение в 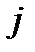-го период, то штрафа за отказ в этот период не будет. Оба описанных момента можно отразить посредством функции

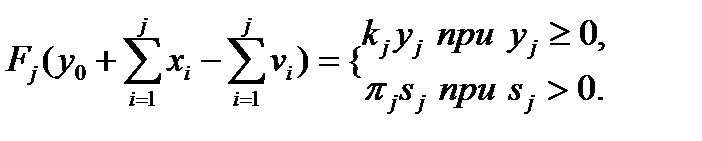( 1.4.3)

где , 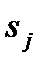определяются выражениями (1.4.1) и (1.4.2) соответственно.

Суммарные расходы склада за 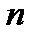периодов с учетом равенств (1.4.3) можно записать в виде

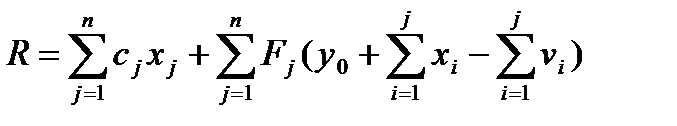. (1.4.4)

Поскольку спрос 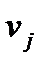- случайная величина, выражение (1.4.4) является функцией случайной величины 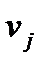. Найдем математическое ожидание .

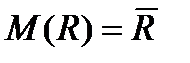Напомним, что если 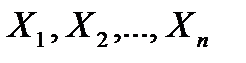- система непрерывных случайных величин с плотностью вероятности 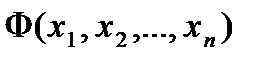, а 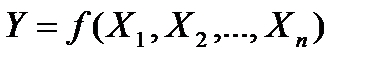- функция этих случайных величин, то математическое ожидание величины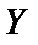

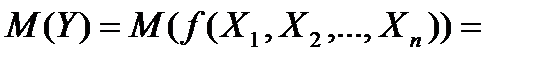
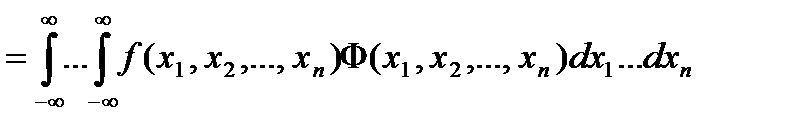(1.4.5)

Если непрерывные случайные величины 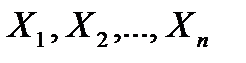независимо распределены с плотностями вероятности 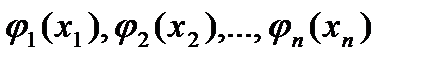, то плотность вероятности 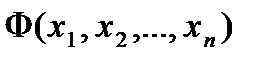появления некоторой определенной комбинации величин 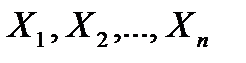равна произведению плотностей вероятности появления каждой из величин, т. е.

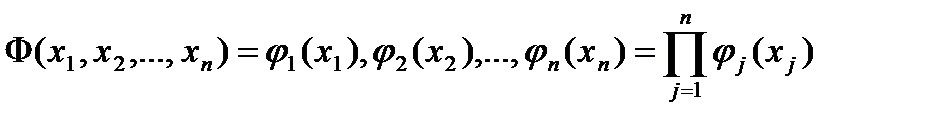. (1.4.6)

С учетом равенства (1.4.6) формула (1.4.5) примет вид

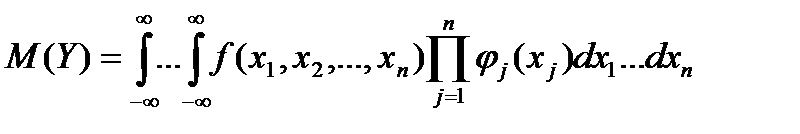. (1.4.7)

Как видно из равенства (1.4.4), в нашем случае 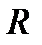есть функция 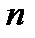независимых непрерывно распределенных на интервале 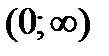с плотностями вероятности 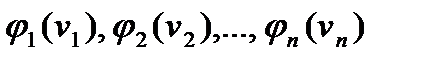случайных величин 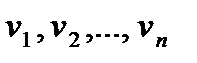. Поэтому в соответствии с формулой (1.4.7) математическое ожидание 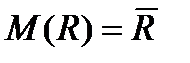функции

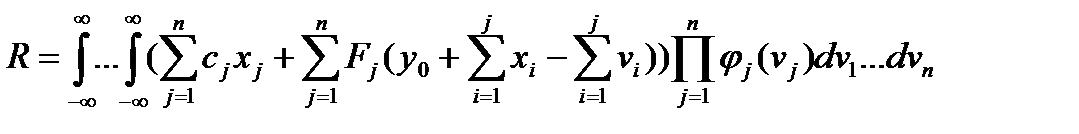. (1.4.8)

Функция (1.4.8) выражает математическое ожидание расходов склада за 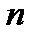периодов. Задача состоит в выборе 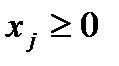, минимизирующих .

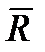Сразу выбрать все 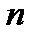значений 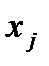нельзя. В самом деле, решение о том, какое количество продукта следует заказать в начале, например, второго периода, зависит от того, какое количество продукта было завезено на склад и каков был спрос в течение этого периода, т. е. оптимальное значение 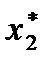является функцией 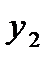- запаса в начале второго периода. Аналогично дело обстоит для любого 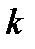-го периода, т. е. 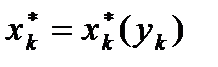. Такой подход к решению соответствует концепции метода динамического программирования: решение на каждом шаге(периоде) выбирается исходя из результатов предыдущего шага (периода).