Решение задач линейного программирования с помощью excel

1 Цель лабораторной работы

Научиться составлять математическую модель и находить оптимальное решение.

2 Задание (пример) к лабораторной работе

Решить задачу распределения ресурсов. Определить, в каком количестве надо выпускать продукцию каждого типа, чтобы получить максимальную прибыль. Для этого необходимо выполнить следующее:

1. Создать форму для ввода условий задачи.

2. Ввести исходные данные в виде таблицы.

3. Ввести в отдельные ячейки таблицы зависимости из математической модели.

4. Найти оптимальное решение с помощью команды Поиск решения/меню Сервис.

5. Получить оптимальное решение задачи распределения ресурсов, вывести на экран три типа отчетов: по результатам, по устойчивости, по пределам и тщательно проанализировать их.

6. Привести свои выводы и предложения по поводу получившихся результатов оптимизации данной задачи.

Исходные данные

Выпускается продукция четырех типов: продукт 1, продукт 2, продукт 3, продукт 4.

· Для выпуска требуется 3 вида ресурсов: труд, сырье, финансы.

Известно:

· Нормы расхода (количество ресурса каждого вида), необходимые для выпуска единицы продукции данного типа.

· Сколько ресурса имеется в наличии.

· Прибыль, получаемая от реализации единицы каждого типа продукции.

Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы.

Оформим данные в виде таблицы 1:

Таблица 1 - Таблица представления результатов

Ресурс	Продукт 1	Продукт 2	Продукт 3	Продукт 4	Знак	Наличие
Прибыль					мах
Трудовые					<=
Сырьевые					<=
Финансовые					<=

Постановка математической задачи

Введем обозначения:

Xj- количество выпускаемой продукции j- го типа (j=1…4); Bi- количество имеющегося в наличие ресурса i-го вида (i=1…3) ; Aij- норма расхода i- го ресурса для выпуска единицы продукции j-го типа; Сij- прибыль, получаемая от реализации продукции j- го типа.

F=60x₁+70x₂+120x₃+130x₄ ®max

x₁+x₂+x₃+x₄<=16

6x₁+5x₂+4x₃+3x₄<=110

4x₁+6x₂+10x₃+13x₄<=100

хj >= 0, j=1,2,…,4.

Ход выполнения лабораторной работы

1 На рабочем листе EXCEL подготовим форму для ввода условий задачи: Для этого в ячейку D1 введем слово Переменные, в D7 – Ограничения.

Далее в диапазон клеток B2:E3 ввести соответственно: Продукция 1, Продукция 2, Продукция 3, Продукция 4 (введите в ячейку B2 Прод1 и щелкнув мышкой по прямоугольнику внизу ячейки протяните до Е3. Вводим в ячейку A2 Имя, в А3- значение, А4 – нижняя граница, А5 – верхняя граница, А6 – коэффициенты в целевой функции и т. д., как указано в таблице 1.

Весь этот текст является комментарием и на решение задачи не влияет.

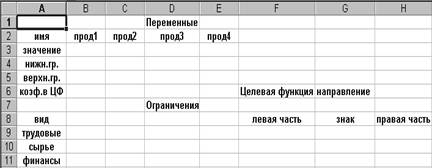
Рисунок 1 – Компьютерный эквивалент задачи

2 Введите исходные данные в форму.

3 Далее введите зависимости для целевой функции и левой части ограничений:

- Курсор ставим в клетку F6, выбираем команду Мастер функций на панели инструментов и щелкаем левой кнопкой мыши. На экране появляется диалоговое окно Мастер функций шаг 1 из 2. Устанавливаем курсор в окно Категория на категорию Математические функции, щелкаем левой кнопкой мыши и выбираем курсором в окне Функции Суммпроизв. Щелкаем на кнопку мыши.

Нажимаем на команду Далее. Открывается диалоговое окно Мастер функций, где в строке массив 1 вводим диапазон ячеек B$3:E$3. Следует заметить, что во все диалоговые окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.

В массив 2 ввести B6:E6. Затем щелкаем на кнопку ОК.

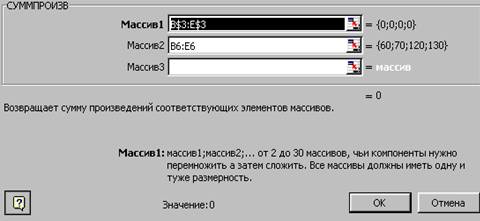Рисунок 2 – Функция MS Excel СУММПРОИЗВ

Устанавливаем курсор в клетку F6 и копируем эту формулу в диапазон F9:F11.

На этом ввод данных закончен.Он оформляется в виде (3):

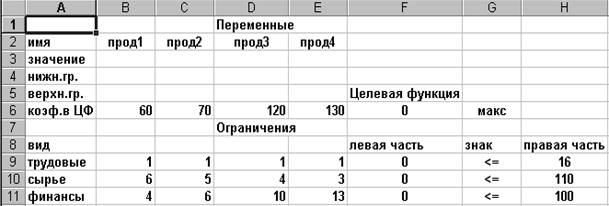Рисунок 3 – Итоговая таблица ввода исходных данных

4 Организация поиска решений.

В меню Сервис выбираем команду Поиск решения. Следующие действия производятся в диалоговом окне.

Уставить целевую ячейку (щелкнуть мышкой в F6)

В этом же диалоговом окне указываем, какое значение должна принимать целевая функция (максимальное или минимальное).

Вводим адреса искомых переменных, для этого ставим курсор в поле Изменяя ячейки и вводим адреса: B3:E3.

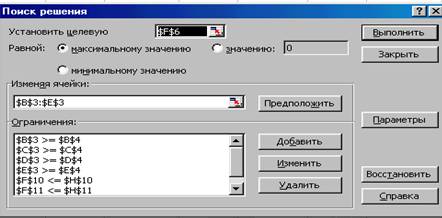Далее нажмите кнопку Добавить.

Рисунок 4 – Окно ПОИСК РЕШЕНИЯ

На экране появится диалоговое окно Добавление ограничения.

Рисунок 5 – Окно ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ

Вводим граничные условия на переменные.

В окне Ссылка на ячейку ввести B3. Курсор устанавливаем на стрелку и щелкаем на левую кнопку мыши. Устанавливаем курсор на знак >= и щелкаем на левую кнопку мыши. Переводим курсор в правое окно и вводим там B4. Щелкаем мышкой на команду Добавить. На экране опять появится диалоговое окно Добавление ограничения. Аналогично вводим граничные условия для остальных переменных.

$B$3>=$B$4

$C$3>=$C$4

$D$3>=$D$4

$E$3>=$E$4

Аналогично вводим и другие ограничения:

F9<=H9, F10<=H10, F11<=H11.

После ввода последнего ограничения вместо Добавить ввести Ок. На экране появится диалоговое окно Поиск решения с введенными условиями.

Если при вводе задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делается с помощью команд Изменить…, Удалить.

На этом ввод условий задачи заканчивается. На очереди следующий шаг – решение задачи.

Решение задачи производится сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения.

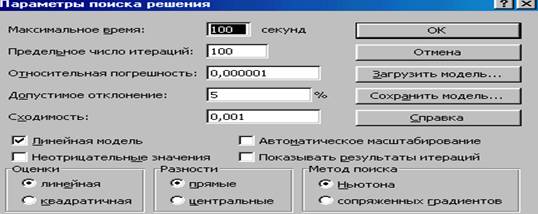Выбираем опцию Параметры… На экране появляется диалоговое окно Параметры поиска решения.

Рисунок 6 – Окно ПАРАМЕТРЫ ПОИСКА РЕШЕНИЯ

-- С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех классов. С наиболее важными командами, применимыми при решении конкретных задач, мы будем знакомиться по мере необходимости. Вместе с тем, команды, используемые по умолчанию, подходят для решения большей части практических задач.

-- Устанавливаем флажок Линейная модель, что обеспечивает применение симпликс – метода.

-- Ок.

-- На экране появляется уже знакомое диалоговое окно Поиск решения.

-- Выполнить.

На экране: диалоговое окно Результаты поиска решения. Решение найдено и результат оптимального решения задачи приведены в таблице.

Рисунок 7 – Окно РЕЗУЛЬТАТЫ ПОИСКА РЕШЕНИЯ

На экране появляется оптимальное решение. Оно представлено в виде таблицы 2:

Таблица 2 - Оптимальное решение задачи линейного программирования

			Переменные
имя	прод1	прод2	прод3	прод4
значение
нижн.гр.
верхн.гр.					Прибыль	направление
прибыль						макс
			Ограничения
вид					левая часть	знак	правая часть
трудовые						<=
сырье						<=
финансы						<=