Математическое дисконтирование

Математическое дисконтирование связано с определением так называемого современного, или приведенного, значения PV на некоторый момент времени, которое соответствует заданному значению FV в другой момент времени. Простейшая задача - определение суммы вклада PV на основе за данной конечной величины в будущем FV через временной период начислений n под заданную. например, простую ставку процентов:

Дисконтированное значение будущей суммы вклада по простой ставке процентов равно

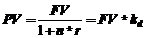(1‑29)

где k_д – дисконтный множитель (коэффициент приведения) для простых процентов. Дисконтный множитель показывает, какую долю составляет первоначальная сумма долга в величине наращенной суммы. k_d = 1/(1 + n*r).

Пример 1‑23

Через 250 дней с момента подписания контракта необходимо уплатить 500 тыс. руб., исходя из 10% годовых и временной базы 360 дней. Определить первоначальную сумму долга.

Решение:

Поскольку срок ссуды менее года, то используем формулу простых процентов:

PV=FV * 1 / (1 + t / T*r ) =

= 500000 * 1 / (1 + 250 / 360 * 0,1) = 467532.5 руб.

PV=FV*k_д = 500000 * 1.0694 = 467532.5 руб..

Таким образом, первоначальная сумма долга составила 467532.5 руб руб., а проценты за 250 дней – 23116.88 руб.

ðДисконтированное значение будущей суммы вклада по сложной ставке процентов равно:

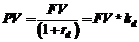(1‑30)

ðЕсли начисление процентов производится m раз в год, то формула примет вид:

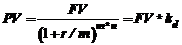(1‑31)

где k_d – коэффициент дисконтирования (приведения)

k_d = 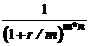(1‑32)

Пример 1‑24

Вы решили через 2 года приобрести автомобиль стоимостью 200000 руб.С этой целью Вы намерены сегодня воспользоваться услугами банка, предоставляющего ссуду под 10% годовых с капитализацией процентов:

а) ежегодно;

б) ежемесячно.

Какая сумма должна быть положена в банк?

Решение

а) 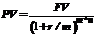= 200000/(1+0.1/1)² = 165289.3 руб.

б) 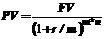=200000/(1+0.1/12)²⁴ =163881.9 руб.

Банковский учет

Банковский учет заключается в покупке денежных обязательств, (на­пример, векселя[13]) банком по цене, которая меньше номинальной указанной в ней суммы[14]. В этом случае говорят, что вексель учитывается и клиент получает сумму:

PV = FV -D, ( 1‑33)

где FV - номинальная сумма данного обязательства; PV - цена покупки век­селя банком; D - дисконт, сумма процентных денег (доход банка

Схема расчетов по дисконтированию показана на рис.4-8 для случая, когда до срока оплаты векселя векселедателем (т.е. тем, кто его выдал) остался год

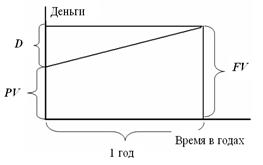
Рис. 1‑8 Схема дисконтирования

Для расчета дисконта могут быть использованы как простая, так и сложная учетные ставки.

FПростая учетная ставка[15]:

D = FV - PV = FV * n * d = FV * t / T * d , ( 1‑34)

где n – продолжительность срока в годах от момента учета до даты выплаты известной суммы в будущем.

Отсюда:

PV = FV - FV * n * d = FV * (1 - n * d)[16] = FV*кd ( 1‑35)

где k_d = (1 - n * d) – дисконтный множитель.

Очевидно, что чем выше значение учетной ставки, тем больше дисконт.

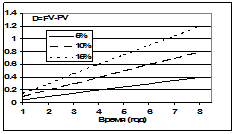
Рис. 1‑9 Зависимость величины дисконта от величины простой учетной ставки

Пример 1‑25

Вексель выдан на 5000 руб. с уплатой 17 ноября, а владелец учел его в банке 19 августа по учетной ставке 8%. Определить сумму, полученную предъявителем векселя и доход банка при реализации дисконта.

Решение:

Для определения суммы при учете векселя рассчитываем число дней, оставшихся до погашения обязательств:

t = 13 (август) + 30 (сентябрь) + 31 (октябрь) + 17 (ноябрь) - 1 = 90 дней.

Отсюда, определяемая сумма:

PV = FV * (1 - t / T *d) = 5000 (1 - 90 / 360 * 0,08) = 4900 руб.

Тогда дисконт составит:

D = FV - PV = 5000 - 4900 = 100 руб.

или

D = FV *( t/T * d )= 5000 * 90 / 360 * 0,08 = 100 руб.

Следовательно, предъявитель векселя получит сумму 4900 руб., а банк при наступлении срока векселя получит дисконт в размере 100 руб.

FСложная учетная ставка:

PV = FV *(1 - d)ⁿ ( 1‑36)

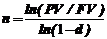(1‑37)

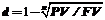( 1‑38)

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, т.к. учетная ставка каждый раз применяется к величине, уменьшаемой на величину дисконта.

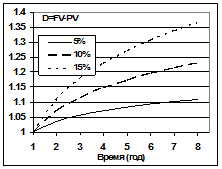
Рис. 1‑10 Зависимость дисконта от величины сложной учетной ставки.

Пример 1‑26

Вексель на сумму 100 тыс. руб. и сроком платежа через 3 года продан с дисконтом по сложной учетной ставке 30% годовых.

Какова сумма дисконта и современная величина платежа?

Решение

PV = FV*(1-d)ⁿ =100000*(1-0.3)³ = 34300 руб.

D =FV-PV = 100000 – 34300 = 65700 руб.

Пример 1‑27

Заемщик должен возвратить кредитору долг в сумме 1 млн. 200 тыс. руб. Первоначальная сумма была выдана заемщику ссудой в размере 1 млн. руб. под 50% годовых, начисляемых по сложной учетной ставке. На какой срок заемщику выдавалась ссуда, если T=360 дней?

Решение.

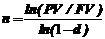= ln(1/1.2)/ln(1-0.5) = 0.263 года @ 94 дня.