Расстановка компенсирующих устройств.
Суммарная мощность компенсирующих устройств опред-ся из баланса реактивной мощности: Qс=Qн+∆Q- Qку.
Реактивная мощность на каждой п/с: Qi=Pi*tg 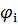 ,где
,где 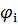 -угол для п/с без компенсации.
-угол для п/с без компенсации.
Qбал= 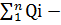 Qку
Qку 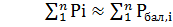
С учетом балансирующей мощности рассчитаем tg 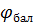 =
= 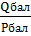
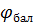 - для всех п/с должен быть одиноков.
- для всех п/с должен быть одиноков.
Для каждой п/с: Qкуi= Qi- Qбал,i (округляется до ближайшего стандартного большего)
В радиальных сетях может быть использованна простейшая методика:
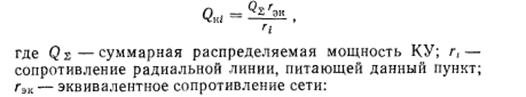
Вводится либо ограничение,либо уравнение ограничение в решаемую систему нелинейных уравнений.
При установке КУ потери мощности могут снизиться на 25%.
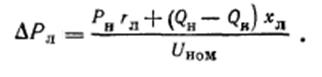
КУ устанавливается на тех п/с,где напряжение невозможно поддерживать за счет уентрализованного регулирования.
Применение оптимизации и ситемного подхода при компенсации реактивной мощности.
Компенсация Q в электроэнергетических системах применяется для снижения потерь мощности и регулирования напряжения.
∆U,a= 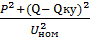 *r
*r
Рст=Рн+∆Р.
∆Р 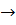 min-задача оптимизации.
min-задача оптимизации.
Допущения:
1)Считаем ток в узле нагрузки неизменимым;2)КУ не влияют на режим U;3)Не учитывается изменение удельной стоимости потерь;4)Стоимость КУ зависит от мощности З=Зуд*QКУ;
Компенсация реактивной мощности в системе-системная задача.
При решении:1)Учитываются взаимосвязи в сети;2)Выполняются допущения;3)Учитываются многокритериальные задачи.
Сети имеют сложную структуру и при оптимизации обычно исп-ся прием эквивалентирования,причем оно должно быть таким,чтобы расчет режима до и после не изменился.
Задача расчета выполняется сверху вниз.

Определение мощности компенсирующих устройств в разомкнутой сети.
Уравнение баланса составляется по одному принципу для простой и разветвл. схемы
P2’’+j Q2’’ P2+j Q2

Qку
Уравнение баланса Q2’’+ Qку= Q2
P1’’+j Q1’’ P2’’+j Q2’’ P2+j Q2

Qку,1 P1+j Q1 Qку,2
Q1’’+ Qку,1= Q1+ Q2’
Q2’’+ Qку,2= Q2
Рассмотрим расчет мощности КУ с учетом потерь мощности.
Простейшая сеть:
В рез-те расчетов устоновившегося режима известно U2, U1 в ЦП заданно.
Можем пренебречь поперечной сост-й реактивн. мощности:
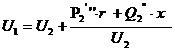
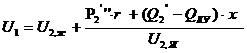
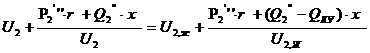
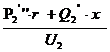
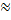
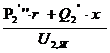
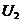
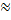
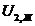
Сделаем допущение:
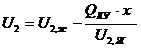
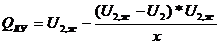
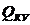 =f(U)
=f(U)
Определение мощности компенсирующих устройств в сложных сетях.
Рассмотрим кольцевую схему.
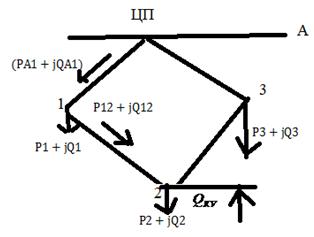
Требуется установить 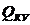 .
.
Расчитаем установившийся режим:
SA1= 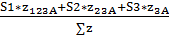
Допустим сеть однородная (отношение индуктивного сопротивления к активному на всех участках одинаково)
Считаем x 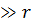
SA1,КУ= 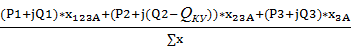 = SA1-
= SA1- 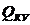 *
* 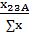 = SA1-
= SA1-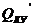
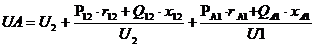
С учетом КУ:
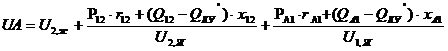
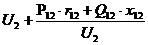 +
+ 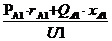 =
= 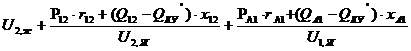
Допущения:
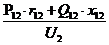
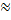
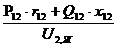
Выражение принимает вид:
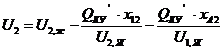 ’
’
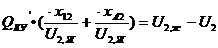
В кольцевых сетях 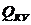 зависит от U и от параметров.
зависит от U и от параметров.
Распределение мощности компенсирующих устройств в сложных сетях.
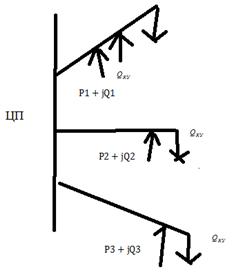
Рассмотрим сеть.
В таких задачах min затраты по всей сети.
Реактивная мощность определ-ся активным сопротивлением сети:
∆Q= 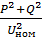 *х; ∆Р=
*х; ∆Р= 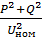 *r/
*r/
Приведенные затраты для всей сети:∆З=∆З1+∆З2+∆З3= 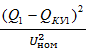 *х1*
*х1* 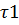 *b0+
*b0+ 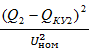 *х2*
*х2* 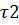 *b0+
*b0+ 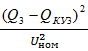 *х3*
*х3* 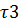 *b0
*b0 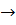 mln.
mln.
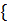 V=∆З+λ
V=∆З+λ 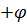
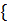 Qк∑-Qкi= 0
Qк∑-Qкi= 0
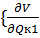 =0
=0
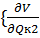 =0
=0
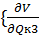 =0
=0
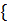 Qк∑-Qкi= 0
Qк∑-Qкi= 0
Условие оптимального распределения компенсирующих уст-в вобщем виде:
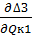 =
=