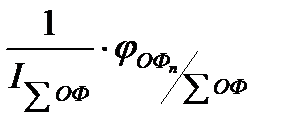Алгоритм цепных подстановок и способ корректировок в табличной форме
Область базисных данных Область фактических данных
| Показатели | База (0) | Подстановка | Подстановка | Подстановка | Факт (1) | ||||
| N | 280=250*1,1200 | 280=250*1,1200 | 280=250*1,1200 | ||||||
| D | 70=50*1,4000 | 70=50*1,4000 | |||||||
| P | 15=16*0,9375 | ||||||||
| B | 1,5 | ||||||||
| X | 44,8=40*1,1200 | 32=40*(1,12/1,4)=40*0,8 | 30=40*IA=40*(IC*Ip/Id)=40*0,75 | ||||||
| DX(N) = +4,8 | DX(d) = -12,8 | DX(p) = -2 DX(b) = +10 | |||||||
| DX=0 | |||||||||
Постановка задачи:
(1) (2)
Х = А/b 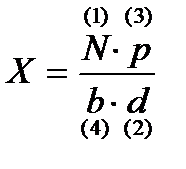
(1) (2)
A = C*p
(1) (2)
C = N/d
Если «n» – число первичных факторов (равно числу корректировочных коэффициентов) n = 4 (не ограничивается);
[n-1] – количество этапов детализации – равно числу корректировочных коэффициентов (I) по количественным параметрам;
+ [1] – корректировочный коэффициент по результативному показателю;
[1] – Х0 базисный уровень результативных показателей;
[n+1] –общий объем необходимой информации.
4. Суть алгоритма анализа:
| А |
| b |
| X |
I уровень детализации
(4) II уровень детализации
| С |
| p |
(3) III уровень детализации
| N |
| d |
(1) (2)
DХ(р) = Х0*(IА-IС)
DХ(d) = Х0*(IC-IN)
Алгоритмические шаги:
1) выбор субсистемы, включающий конкретный фактор;
2) см. схему выше.
Все способы последовательного элиминирования взаимосвязаны и являются соответствующей модификацией путем алгебраических, логических, статистических упрощений.
Одноименные результаты пофакторного анализа выполненные разными способами элиминирования должны быть одинаковыми (в определенных пределах). При аналитической проверке балансовым способом допускается дисбаланс не более 2–3% от общего измерения результативного показателя (DХ).
DХº 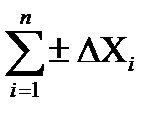
Алгоритм корректировочных коэффициентов может быть реализован в виде разности двух подстановок. В этом случае подстановки рассчитываются и имеют другой вид по отношению к цепным.
Подстановка – это базисный результативный показатель скорректированный на индекс соответствующего количественного фактора системы.
Для правильного выбора корректировочных коэффициентов необходимо:
1) выбрать простую формулу взаимосвязи (субсистему);
2) для первой подстановки в алгоритме берется корректировочный коэффициент результирующего показателя субсистемы;
3) для второй подстановки – коэффициент по количественному фактору субсистемы.
Влияние любого фактора на изменение результативного показателя определяется как умножение базисного уровня результирующего показателя всей системы на разность корректировочных коэффициентов результативного показателя и первого количественного фактора субсистемы.
5. Аналитическая проверка может быть реализована в трех вариантах (алгоритмах):
1) при выполнении комплексного анализа, т.е. по всем параметрам факторной системы – балансовый способ:
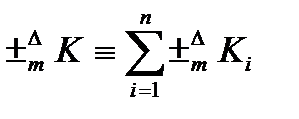
Общее изменение результирующего показателя тождественно равно сумме пофакторных его изменений.
Критерий – допускается дисбаланс на более 2–3%
2) при локальном анализе (отдельно взятый фактор):
а) получение результата другим возможным способом
DК(а)ц.п.ºDК(а)корр. – дисбаланс 2–3%
б) DК(b)
mK(b) – способом относительных величин
º К0 (дано)
К0 (расчетное)= 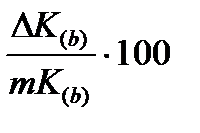 дисбаланс 2-3%
дисбаланс 2-3%
СПОСОБ ОЦЕНКИ ВЛИЯНИЯ СТРУКТУРНЫХ ИЗМЕНЕНИЙ
ВНУТРИ СОВОКУПНОСТИ.
В сложной факторной системе могут присутствовать качественные субфакторы выраженные в средней величине.
Е = V* 
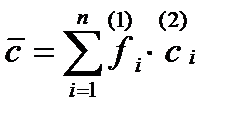
1 уровень DЕ(fi) – в целом по совокупности
2 уровень DЕ(f1;f2;…fi) - по элементам совокупности.
fi = Vi/V
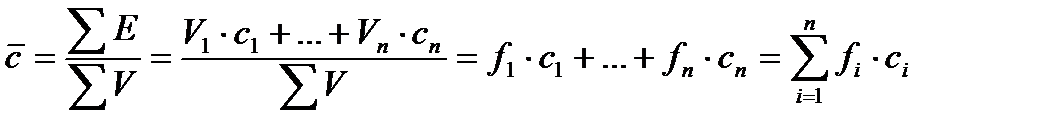 ,
,
E = E1+E2+…+En; V = V1+V2+…+Vn
1. Цель – расчет абсолютного изменения (аналогично ЦП, СР, Корр.)
2. Возможность использования – в сложных мультипликативно- аддитивных зависимостях качественного субфактора, выраженного средней.
3. Исходные данные: на 1 уровне анализа (в целом по совокупности решения задачи) – используется способ корректировок, следовательно необходимо иметь базисную величину результирующего показателя в целом и по элементам совокупности и корректировочные коэффициенты количественного фактора (V) в целом и по элементам:
1 уровень (Е0, Е01, Е02,…Е0n)
(IV, IV1, IV2,…IVn)
На 2 уровне (по элементам совокупности) информационная база отчетная величина количественного фактора в целом, удельного веса планового и отчетного структурного элемента, в целом и по элементам и качественные признаки плановые и отчетные в целом и по элементам:
V1, (fi0,1, ci0,1,  0,1
0,1
4. Суть алгоритма. Алгоритм структурных изменений строится на двух аналитических уровнях:
1 уровень – в целом по совокупности;
2 уровень – отдельно по элементам совокупности.
Аналитическая постановка задачи:
E = V(1)*  (2); E = E1+E2+…+En; V = V1+V2+…+Vn;
(2); E = E1+E2+…+En; V = V1+V2+…+Vn;
Ei = Vi(1)*ci(2); 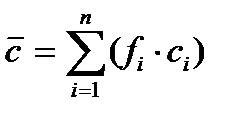 .
.
Схема взаимосвязей:
| V |
| E |
 fi
fi
| V1 |
| E1 |
c1 f1
… … … …
| En |
| Vn |
cn fn
Каналы влияния факторов:
cn ® En Þ E; cn ®  ® E.
® E.
…
| V |
| Объемные показатели |
…
| V1 |
| V2 |
| E |
| Результативный показатель |
| E1 |
| E2 |

c1 c2
| Качественные показатели |
fi
f1 f2
| Структурные коэффициенты |
Аналитическая постановка задачи:
1 уровень (в целом по совокупности) – алгоритм структурных изменений представляет собой алгоритм цепных подстановок.
fi ®  ® K
® K
 0
0  *
*  1
1
åfi0*ci0 åfi1*ci0 åfi1*ci1
DЕ(fi,ci) = D  ( fi) + D
( fi) + D  (ci) *V1
(ci) *V1
D 
DE(fi) = V1*D  (fi) = V1*[åfi1*ci0 - åfi0*ci0]
(fi) = V1*[åfi1*ci0 - åfi0*ci0]
Все качественные показатели и структурные коэффициенты нужно выразить через количественные показатели:
f0,1 = Vi0,1/V0,1; ci0,1 = Ei0,1/Vi0,1;
DE(fi) 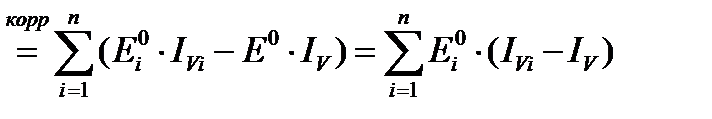 .
.
Для оценки влияния структурных изменений в целом по совокупности используется алгоритм способа корректировок.
Относительное изменение определяется через абсолютный результат по трёх компонентной формуле:
±mE(fi) = 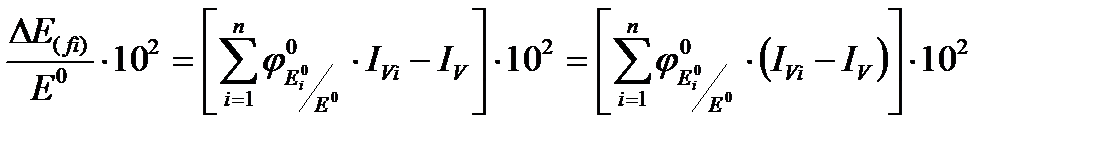
где 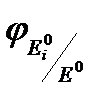 – базисное соотношение результативного показателя (Е) по элементам совокупности и в целом.
– базисное соотношение результативного показателя (Е) по элементам совокупности и в целом.
Чем больше разность (IVi-IV), тем больше результат влияния структурных изменений на изменение результативного показателя.
5. Проверка осуществляется балансовым способом.
_________
2 уровень (отдельно по элементам совокупности)
Общая постановка задачи:
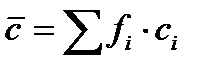
DE(fn) = V1*D  (fn)
(fn)
Таблица 2
| Элементы совокупности | Оценка влияния факторов: | Итого | ||
структурных изменений [D  (fi)] (fi)] | качественных признаков [D  (сi)] (сi)] | |||
| 1й | ±Df1*(c01-  0) 0) | ±Dc1*f11 | D  (f1;c1) (f1;c1) | D  (1й эл-т) (1й эл-т) |
| 2й | ±Df2*(c02-  0) 0) | ±Dc2*f12 | D  (f2;c2) (f2;c2) | D  (2й эл-т) (2й эл-т) |
| … . | … | … | … | |
| nй | ±Dfn*(c0n-  0) 0) | ±Dcn*f1n | D  (fn;cn) (fn;cn) | D  (nй эл-т) (nй эл-т) |
| Всего | 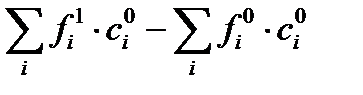 | 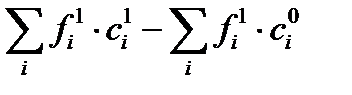 | D  |
Для получения результата изменения общего результирующего показателя от влияния структурных изменений (в любой группировке) содержание любой ячейки данной таблицы нужно умножить на фактическое значение количественного параметра:
DЕ(fn; cn) = V1*D  (fn; cn).
(fn; cn).
Доля влияния соответствующего фактора (d) на результирующий показатель равнозначна отношению абсолютного/относительного изменений по фактору к общему изменению результативного показателя.
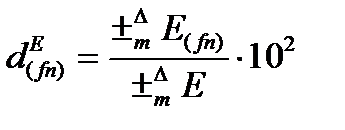
Относительное изменение от влияние n-го элемента:
mE(fn) = [±Dfn%*(cn0/c0 - 1)*IV]
например, 1,2; 0,8;…
Оценка влияния структурных изменений способами последовательного элиминирования  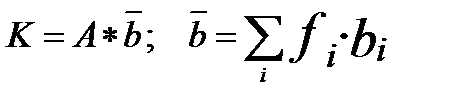 |
В целом по совокупности 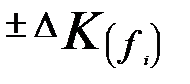 |
По элементам совокупности 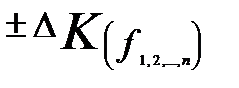 |
| Способ корректировок |
| Способ структурных изменений |
| Способ структурных изменений |
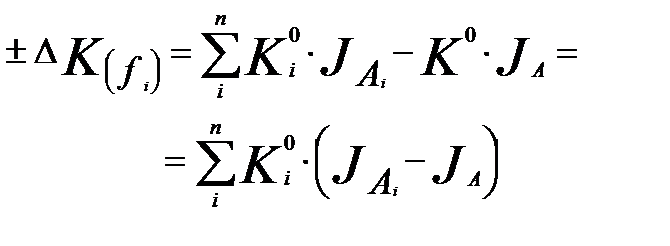 |
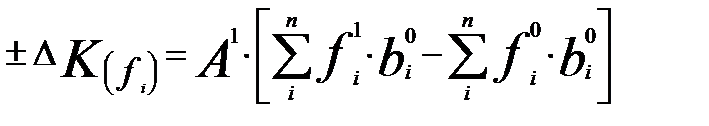 |
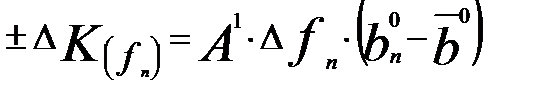 |
 Алгоритмы расчета относительных изменений результативного показателя от влияния структурных изменений по формуле: Алгоритмы расчета относительных изменений результативного показателя от влияния структурных изменений по формуле: 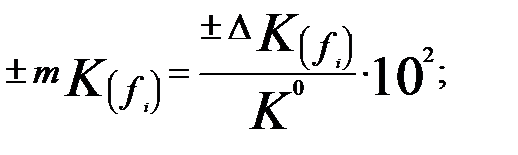 |
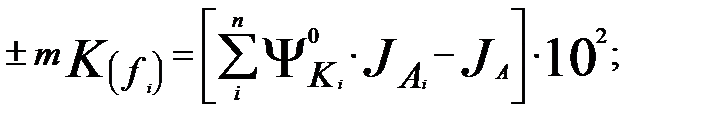 |
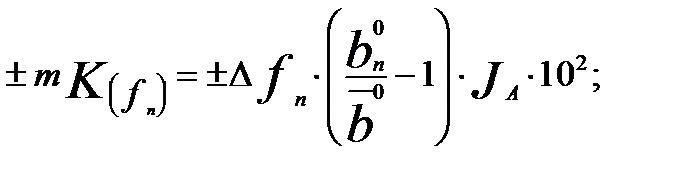 |
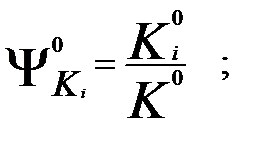 |
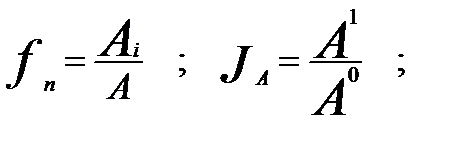 |
СПОСОБ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН (ОВ).
1. Расчет относительных изменений.
2. Возможность применения: отдельно для мультипликативных и аддитивных связей:
а) для мультипликативной и для кратной – ограничений нет;
б) для аддитивной связи прием используется только при прямой зависимости. При обратной зависимости – НЕЛЬЗЯ!
3. а) для мультипликативных связей:
– при прямом факторном анализе исходная информация состоит из следующего:
«n» – число первичных факторов;
(n-1) – количество этапов детализации;
(n+1) – всего параметров в системе;
[n -1] – число коэффициентов (%) по количественным параметрам;
[1] – коэффициент (%) по результирующему показателю.
n-1+1 = [n] – общий объем исходных данных.
– при обратном факторном анализе кроме изложенного может быть добавлена информация по качественным признакам (темпы прироста по качественным факторам).
б) для аддитивной (прямой) связи кроме изложенного в п.3а) ввиду необходимости признаки (коэффициенты):
А = В + С
IА = IВ* 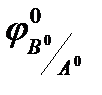 + IС*
+ IС* 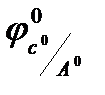
1) 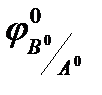 и 2)
и 2) 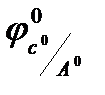 – два признака, т.к. два параметра (слагаемых).
– два признака, т.к. два параметра (слагаемых).
Информационная база «n»+«к»,
где «к» – число факторов-слагаемых аддитивной модели.
4. Сущность алгоритма целесообразно показывать по каждому типу взаимосвязи (6 вариантов).
1 вариант. Простая прямая мультипликативная.
А = В(1) * c(2)
±mA(B) = (IB–1)*102=mB – влияние 1-го фактора равно темпу его прироста.
+
±mA(C) = (IA – IB)*102 = (IB*IC – IB)*102 = mc*IB
±mA = (IA – 1)*102
mA(С) = mc*IB
При заданном значении mC = ±5%
mc = mA(C)/IB – получаем результат (прогнозный)
2 вариант. Простая обратная мультипликативная связь – в обратной зависимости 1-й фактор по рангу (количественный)
М = В(2)/N(1) IM = [1/IN]*IB
mM(N) = ( 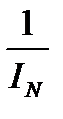 – 1)*102 = – (±mN)*
– 1)*102 = – (±mN)* 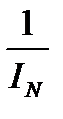
+
показывает наличие обратной связи
º mM(B) = (IM – 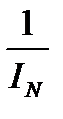 )*102 = ±mB*
)*102 = ±mB* 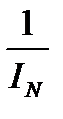
mM = (IM – 1)*102
3 вариант. Простая обратная мультипликативная связь – в обратной зависимости 2-й фактор по рангу (качественный)
Полная аналогия с 1 вариантом.
М = В(1)/N(2)
mM(B) = mB
mM(N) = (IM – IB)*102 = ( 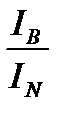 – IB)*102 = – (±mB)*IM
– IB)*102 = – (±mB)*IM
Использование способа относительных величин при обратной зависимости факторной модели имеет особенности (микромодуль), если в обратной зависимости 1-й фактор.
mM(B) = 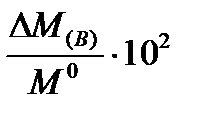
4 вариант. Сложная (более 3-х факторов) мультипликативная связь.
| A |
| C |
| X |
| M |
| D |
А = C(1)/р(2)
b = М(1)*D(2) (1) (2)
b
(1) (2) (1) (2)
p
(1) (2) (3) (4)
Реализация этого алгоритма осуществляется в виде двух правил под названием свойства относительной величины:
1. Изменение результирующего показателя от влияния первичных факторов (С и р) по величине и знаку равны изменению субфактора (А) от их влияния.
2. Для определения результата влияния первичных факторов на результирующий показатель (М и D) необходимо относительное изменение субфактора (b) умножить на IA, т.е. первый фактор.
| 1-ое свойство |
+
mX(p) = mA(p) = (IA – IC)*102 = – mp*IC
º
mX(A) = mA = (IA – 1)*102
º
| 2-ое свойство |
+
mX(D) = mb(D)*IA = (Ib - IM)*IA*(-102) = – mD*Ib*IA= – mD*IX
º
mX(b) = (IХ – IА)*102 = mb* IA
mX = (IX – 1)*102 = mX
5 вариант. Прямая простая аддитивная зависимость.
А = В + С
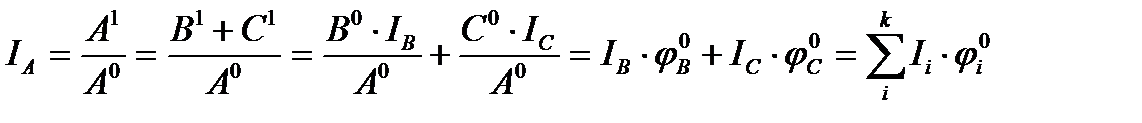
mA = (IA – 1)*102
IA – 1 = 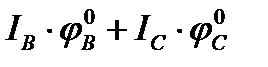 = [
= [ 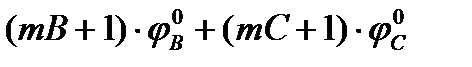 ]
]
mA = 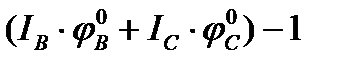 = [
= [ 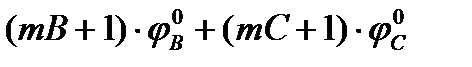 ] – 1 =
] – 1 = 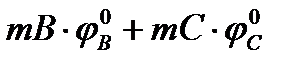
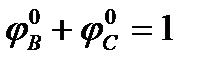 |
mA(B) = mB* 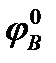
+
º mA(C) = mC* 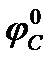
mA = (IA – 1)*102
6 вариант. Сложная, прямая, аддитивная зависимость.
A = B 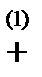 C
C
B = D(1)*p(2)
C = N(1)*e(2)
mA(D) = mB(D)* 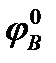 = mD*
= mD* 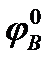 = (ID – 1)*
= (ID – 1)* 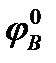 *102
*102
+ +
mA(p) = mB(p)* 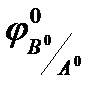 = (IB – ID)*
= (IB – ID)* 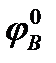 *102 = mp*ID*
*102 = mp*ID* 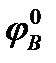
º
mA(B) = mB* 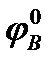
º mA(N) = mC(N)* 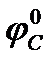 = mN*
= mN* 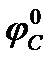 = (IN – 1)*
= (IN – 1)* 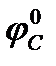 *102
*102
+
mA(e) = mC(e)* 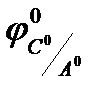 = (IC – IN)*
= (IC – IN)* 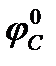 *102 = me*IN*
*102 = me*IN* 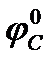
º
mA(C) = mC* 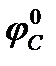
mA = (IA – 1)*102
При аддитивной зависимости следует учитывать следующие нюансы:
- обязательно наличие в качестве информационной базы коэффициентов их количество равно числу факторов слагаемых;
- при аддитивной зависимости необходимо и достаточно получить результат изменения субфактора от влияния первичного.
СПОСОБ ДОЛЕВОГО РАСПРЕДЕЛЕНИЯ –
ДОЛЕВОГО УЧАСТИЯ (ДУ).
1. Цель анализа – определение абсолютного изменения, что тождественно разложению по факторам абсолютного прироста (±D) результирующего показателя.
2. Возможность применения:
- при обратной аддитивной зависимости – ОБЯЗАТЕЛЬНО этим способом (другие способы не используются);целесообразно использовать этот способ ввиду его простоты;
- при сложной мультипликативной зависимости, когда сложный субфактор находится в обратной зависимости с результативным показателем;
- когда есть в готовом виде, когда в качестве исходной информации используются результаты оценки влияния первичных факторов на изменение субфакторов;
- при сложных обратных зависимостях мультипликативного и аддитивного типа.
3. Исходная информация:
корр ц.п., с.р .
[(n+1)] £ ИБ £ [2*(n+1)]
min max
ИБ – информационная база;
n – первичные факторы.
ИБ зависит от того какие способы элиминирования используются на отдельных (промежуточных) этапах общего алгоритма д.у.
4. Суть алгоритма:
1) сложная мультипликативная зависимость
рабочий парк вагонов 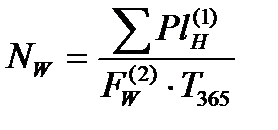
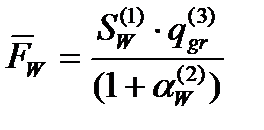
±DNW(Sw, aw, qgr)
1 этап
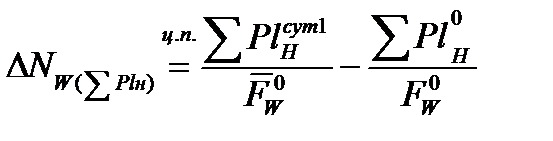
+
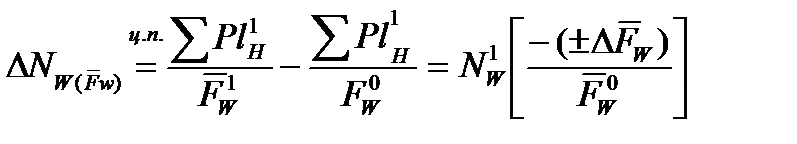
DNW
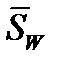 qgr aW
qgr aW
2 этап
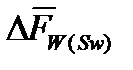
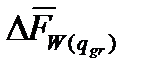
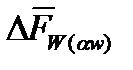
3 этап
| + |
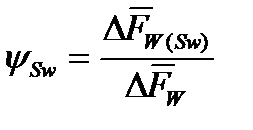 ;
; 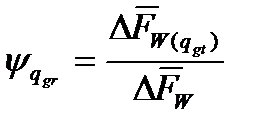 ;
; 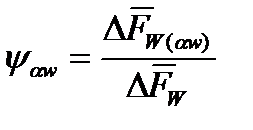
4 этап
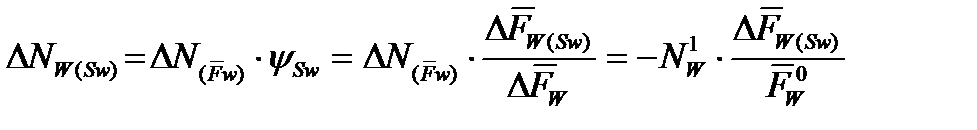
при 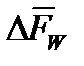 =0
=0
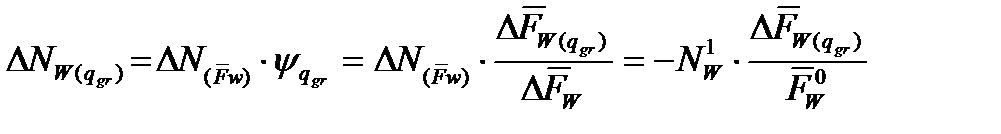
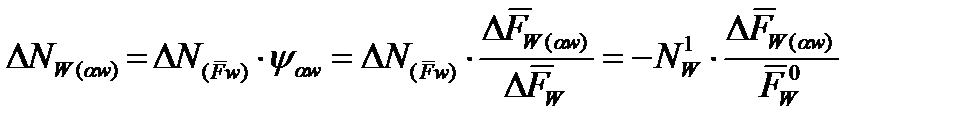
Суть:
1) 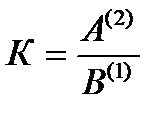 , то DК(С) = – К0×
, то DК(С) = – К0× 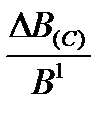 ±mK(C) = – (±) mB(C)×
±mK(C) = – (±) mB(C)× 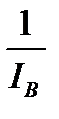
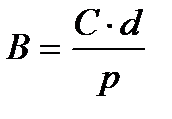
2) 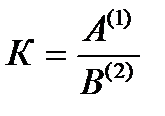 , то DК(С) = – К1×
, то DК(С) = – К1× 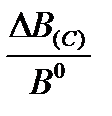 ± mK(C) = - ± mB(C) IK
± mK(C) = - ± mB(C) IK
При изменении рангов на противоположные в исходной аналитической формуле (1,2/ 2,1) в конечном виде алгоритма д.у. индексация или уровни факторов тоже меняются на противоположные.
Относительное изменение:
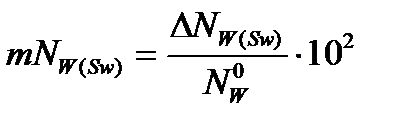
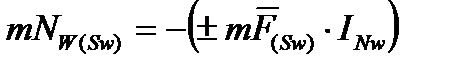
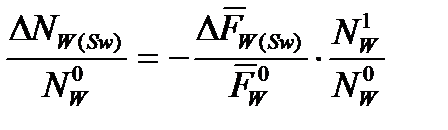
2) сложная аддитивная обратная зависимость
Для прямой зависимости используется способ разниц (д.у. не применяется).
фондоотдача 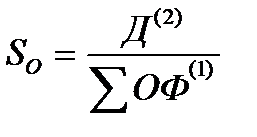
åОФ = ОФ1 + ОФ2 + … +ОФn
1 этап
/> 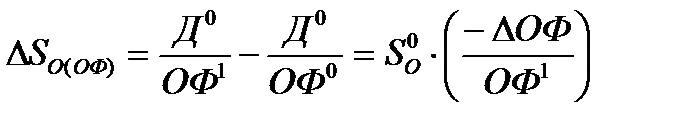
+
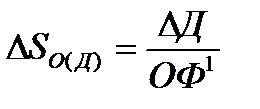
º
DSО = SО1 – SО0
2 этап
DåОФ(ОФ1) = DОФ1
……………………
DåОФ(ОФn) = DОФn
3 этап – расчет коэффициентов
долевого распределения
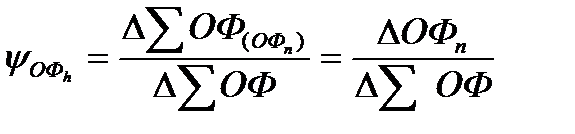
4 этап
DSО(ОФn) = DS(åОФ)×ψОФn = DSО(åОФ)× 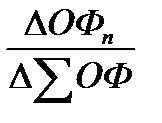 Þ
Þ
при åОФ = 0 – алгоритм некорректен
Þ 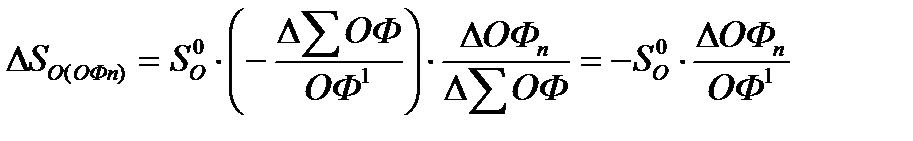
обратная зависимость
mSO(ОФ) = – (±mОФn)×