Количественные показатели динамики развития экономических процессов

Изучение отдельных показателей, характеризующих процесс, недостаточно для получения целостной картины развития сложных систем. Комплексный анализ наряду с изучением динамики одномерных наблюдений предполагает рассмотрение зависимостей между разными показателями системы. К показателям динамики в экономическом анализе можно отнести прежде всего показатели роста и прироста.

Показатели прироста.Приростами временного ряда называются разности между последующими и предыдущими его уровнями

.

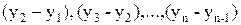Если развитие исследуемого процесса происходит равномерно с постоянным приростом, то целесообразно использовать показатель среднего абсолютного прироста

.

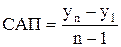Формула представляет собой среднее арифметическое всех приростов ряда. Средний абсолютный прирост представляет собой скорость развития явления во времени. При анализе временных рядов используют также относительные показатели прироста, которые называют темпами прироста. Темпы прироста показывают, на сколько процентов уровень одного периода увеличился (уменьшился) по сравнению с уровнем другого периода. Различают цепные и средние темпы прироста. Цепные показатели рассчитывают по формуле

,

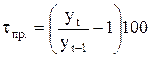для расчета средних темпов прироста можно использовать, например, две крайние точки ряда

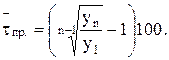
Показатели роста.Сопряженными к показателям прироста считаются показатели роста. Они могут быть базисные, цепные и средние.

Базисные коэффициенты роста представляют собой отношение уровней временного ряда к одному и тому же уровню, выбранному в качестве базисного. Если эти коэффициенты измеряются в процентах, то они называются базисными темпами роста.

Цепные коэффициенты роста рассчитываются как отношение последующих уровней ряда к предыдущим.

Средний темп роста показателя представляет собой среднее геометрическое цепных темпов роста

.

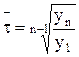Средний темп роста характеризует среднюю скорость изменения изучаемого явления за рассматриваемый период. Зная величины начального уровня и среднего темпа роста, по последней формуле можно вычислить значение любого уровня временного ряда

.

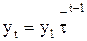Приведенная выше формула для расчета среднего темпа роста обладает существенными недостатками, так как основана на сопоставлении конечного и начального уровней временного ряда, промежуточные уровни во внимание не берутся. Для улучшения формулы предлагается вместо 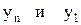рассматривать их сглаженные значения по уравнению кривой роста. В этом случае учитывается колеблемость промежуточных уровней временного ряда. Средний темп роста, полученный таким образом, будет более точно характеризовать изменения изучаемого экономического явления за рассматриваемый интервал времени.

Средний уровень ряда.Это простая и в то же время важная характеристика временного ряда. Расчет среднего уровня ряда производится по формуле простой средней арифметической

.

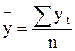Если интервальный ряд имеет неравно отстоящие во времени уровни, то средний уровень ряда вычисляется по формуле взвешенной арифметической средней, где роль весов играет продолжительность времени, в течение которого уровень постоянен

,

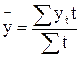где t – число периодов времени, при которых значение уровня 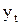не изменяется.

Автокорреляция.В некоторых временных рядах между близко расположенными уровнями существует взаимосвязь. Ее можно наблюдать, если сравнить исходный ряд с рядом, сдвинутым относительно него на несколько шагов вперед. Явление зависимости уровней временного ряда от предыдущих уровней того же ряда называется автокорреляцией.

Классические методы математической статистики применимы лишь в случае независимости отдельных членов ряда между собой. Поэтому при анализе временных рядов чрезвычайно важно установить наличие и степень их автокорреляции. Для определения уровня автокорреляции используется автокорреляционная функция, состоящая из множества коэффициентов корреляции, вычисленных относительно исходного ряда и этого же ряда, сдвинутого на несколько шагов. В случае коротких временных рядов и сдвига на один уровень формула для расчета коэффициентов корреляции имеет упрощенный вид

,

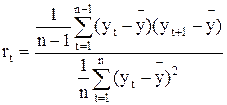где 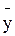– средний уровень ряда.

График автокорреляционной функции называется коррело- граммой и показывает величину запаздывания, с которым изменение показателя сказывается на его последующих значениях.

Автокорреляция характеризует не только взаимосвязь уровней одного и того же ряда, но и степень устойчивости развития процесса во времени, величину оптимального периода прогнозирования и т.п. Устойчивость экономических процессов можно рассматривать как категорию, противоположную колеблемости, и как устойчивость направленности изменений. Во втором случае устойчивость характеризует уровни временного ряда как процесс их направленного изменения. Полной устойчивостью направленного изменения уровней временного ряда следует считать такое их изменение, в процессе которого каждый следующий уровень либо выше всех предшествующих (устойчивый рост), либо ниже (устойчивое снижение). Всякое нарушение такой ранжировки уровней свидетельствует о неполной устойчивости их развития.

Литература

1. Гармаш А.Н., Орлова И.В. Математические методы в управлении: Учеб. пособие. – М.: Вузовский учебник: ИНФРА-М, 2012. – 272 с.

2. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учеб. пособие. – 3-е изд., перераб. и доп. – М.: Вузовский учебник: ИНФРА-М, 2012, 2014. – 389 с.

3. Федосеев В.В., Гармаш А.Н., Орлова И.В. Экономико-математические методы и прикладные модели: учебник для бакалавров / под ред. В.В. Федосеева. – 3-е изд. перераб. и доп. – М.: Издательство Юрайт, 2012. – 328 с.