Конверсия валюты и наращение процентов
Рассмотренные методы наращения процентов позволяют перейти к обсуждению более сложных и важных в практическом отношении задач. Рассмотрим задачу о совмещении операций конверсии (обмена) валюты и наращения процентов.
При возможности обмена рублевых средств на СКВ (Свободно-конвертируемая валюта) и обратной конверсии целесообразно сравнить доходы от непосредственного размещения имеющихся денежных средств в депозиты и опосредованно через другую валюту. Сказанное относится и к получению дохода от СКВ при ее обмене на рубли, депонировании и обратной конверсии.
Возможны четыре варианта для наращения процентов с конверсией денежных ресурсов и без нее:
без конверсии: СКВ → СКВ;
с конверсией: СКВ → Руб → Руб →СКВ;
без конверсии: Руб →Руб;
с конверсией: Руб →СКВ → СКВ →Руб.
В операции наращения с конверсией валют существует два источника дохода — изменение курса и наращение процентов, причем, если второй из них безусловный (так как ставка процента фиксирована), то этого нельзя сказать о первом источнике. Более того, двойное конвертирование валюты (в начале и конце операции) может быть при неблагоприятных условиях убыточным. Решим в связи с этим две задачи. Определим сумму в конце операции и ее доходность для двух вариантов операции с конверсией.
Вариант СКВ →Руб →Руб →СКВ. Примем следующие обозначения:
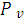 — сумма депозита в СКВ,
— сумма депозита в СКВ,
P — сумма депозита в рублях,
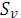 — наращенная сумма в СКВ,
— наращенная сумма в СКВ,
S— наращенная сумма в рублях,
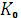 — курс обмена в начале операции (курс СКВ в рублях),
— курс обмена в начале операции (курс СКВ в рублях),
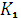 — курс обмена в конце операции,
— курс обмена в конце операции,
n — срок депозита,
i — ставка наращения для рублевых сумм,
j — ставка наращения для конкретного вида СКВ.
Операция предполагает три шага: обмен валюты на рубли, наращение процентов на эту сумму и, наконец, конвертирование в исходную валюту. Конечная (наращенная) сумма в валютe определяется как
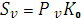 (1+ni)/
(1+ni)/ 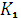 (1.19)
(1.19)
Три сомножителя этой формулы соответствуют трем перечисленным выше шагам. Множитель наращения m с учетом двойного конвертирования здесь имеет вид
m= 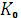 (1+ n i)/
(1+ n i)/ 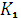 = (1+ n i)/(
= (1+ n i)/( 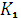 /
/ 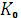 ) (1.20)
) (1.20)
Взаимодействие двух факторов роста исходной суммы в этой формуле представлено наиболее наглядно. С ростом ставки множитель наращения линейно увеличивается, в свою очередь, рост конечного курса обмена уменьшает его.
Пример 15. Предполагается поместить 1000 долл. на рублевом депозите. Курс продажи на начало срока депозита 26,08 руб. за $1, курс покупки доллара в конце операции 26,45 руб. Процентные ставки: i= 22%; j = 15% (360/360). Срок депозита — 3 месяца.
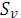 =1000(26,08/26,45)(1+(3/12)(22/100))=1040,2 долл.
=1000(26,08/26,45)(1+(3/12)(22/100))=1040,2 долл.
В свою очередь прямое наращение исходной долларовой суммы по долларовой ставке процента дает
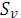 = 1000(1 + 0,25×0,15) = 1037,5 долл.
= 1000(1 + 0,25×0,15) = 1037,5 долл.
1.8 Тестовые задания
1011234. Процентные деньги (проценты) это:
1. Деньги представляемые в долг;
2. Доход от инвестированного капитала;
3. Капитал к его будущей стоимости;
4. Относительная величина дохода.
1022431. Основной капитал это:
1. Сумма долга;
2. Проценты, начисляемые по принципу скидки;
3. Сумма денег дающихся в займы;
4. Вексель, подлежащий оплате.
1033124. Норма процента это:
1. Способ наращения, при котором проценты начисляются на первоначальную сумму;
2. Проценты, начисляемые по принципу наращения на сумму долга;
3. Процесс увеличения денег, предоставляемых в долг;
4. Отношение процента к основной сумме (капиталу).
1042312. Под наращенной суммой ссуды (долга, депозита и др.) понимается:
1. Первоначальная ее сумма с начисленными процентами к концу срока начисления;
2. Увеличение денег, предоставляемых в долг;
3. Всякое уменьшение денег – суммы счета, долга и др.;
4. Сумма денег, инвестированная под проценты.
1053132. Обыкновенный процент, это когда при расчетах процентов используются:
1. Временная база 365/365 дней;
2. Временная база 360 дней;
3. Временная база 360/365 дней;
4. Временная база 365/366 дней.
1063134. Точный процент, это когда при расчетах процентов используются:
1. Временная база 365/365 дней;
2. Временная база 360/365 дней;
3. Временная база 360/360 дней;
4. Временная база 365/366 дней.
1072314. Точный процент с точным числом дней ссуды обозначается как:
1. Временная база 365/365;
2. Временная база 360/365;
3. Временная база 365/360;
4. Временная база 360/360.
1082134. Обыкновенный процент с точным числом дней (банковский) обозначается как:
1. Временная база 365/365;
2. Временная база 360/365;
3. Временная база 365/360;
4. Временная база 360/360.
1093241. Актуарный метод это метод погашения краткосрочных обязательств и предполагает:
1. Последовательное погашение процентов на фактические суммы долга;
2. Если срок ссуды не превышает года, то сумма долга с процентным остатком неизменная до полного погашения;
3. Если срок ссуды не превышает года, то сумма долга с процентным переносится на следующий год;
4. Если срок ссуды превышает год, расчеты делаются для годового периода задолженности.
1101432. В потребительском кредите проценты начисляются:
1. На первоначальную сумму;
2. На основную сумму долга;
3. По договоренности с кредитором, при условии, что кредитор рассчитается по обязательству в полном объеме;
4. На всю сумму кредита, присоединяемую к основному долгу уже в момент открытия кредита.
1112431. Необходимость дисконтирования возникает:
1. При покупке краткосрочных обязательств, без оплаты должником обязательств;
2. При покупке долгосрочных обязательств независимо от срока оплаты;
3. При покупке краткосрочных обязательств, оплата которых должником произойдет в будущем;
4. При продаже долгосрочных обязательств, если обязательства предлагаются под простые проценты.
1121234. Дисконтирование по простым процентным ставкам это когда:
1. По заданной сумме P определяется итоговая сумма S, которая будет накоплена;
2. По заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму ссуды P;
3. Когда прибыль вычисляется по формуле D = Std;
4. Когда инвестор покупает вексель до даты его погашения.
1133312. Математическое дисконтирование это задача, которая формируются так:
1. Какую вторичную сумму ссуды надо выдать в долг, чтобы получить в конце срока проценты в два раза большие, чем первоначально;
2. Какую первоначальную сумму ссуды надо выдать в долг, чтобы получить в конце срока сумму S, при условии, что на долг начисляются проценты по ставке i;
3. Какую первоначальную сумму ссуды надо выдать в долг, чтобы получить в конце срока сумму S, при условии, чтобы на долг проценты не начислялись.
4. Какую первоначальную сумму ссуды надо выдать в долг, чтобы получить в конце срока сумму S, при условии, что на долг начисляются проценты по ставке простого дисконта.
1141432. Выручкой при дисконтировании называется:
1. Первоначальная сумма вместе с процентными деньгами;
2. Всякое уменьшение денег – суммы счета, расчета, долга и так далее;
3. Сумма, остающиеся после вычитания дисконта из первоначальной суммы взятой в долг;
4. Сумма, остающиеся после вычитания дисконта из суммы погашения.
1153312. Банковский или коммерческий учет векселей это метод, по которому:
1. Проценты за пользование ссудой в виде дисконта, когда проценты не начисляются;
2. Проценты за пользование ссудой в виде дисконта начисляются на сумму подлежащею уплате в конце срока по годовой учетной ставке дисконта d;
3. Проценты за пользование ссудой в виде дисконта начисляются на сумму подлежащею уплате в начале срока годовой учетной ставки дисконта d;
4. Проценты за пользование ссудой в виде дисконта, когда проценты начисляются не на всю сумму.
1163321. Процент авансом это:
1. Банковский дисконт
2. Сумма наращения
3. Простой процент
4.Простой процент, который рассчитывается на Р и выплачивается в конце сделки
1171322. Необходимость в расчетах процентной ставки возникает при определении:
1. Финансовой эффективности операции и при сравнении контрактов по их доходности в случаях, когда ставки указаны в явном виде;
2. При покупке краткосрочных обязательств, оплата которых должником произойдет в будущем;
3. Финансовой эффективности операции и при сравнении контрактов по их доходности в случаях, когда процентные ставки в явном виде не указаны;
4. При покупке долгосрочных обязательств, оплата которых должником произойдет в будущем.
1182213. В операции приращения с конверсией валют существуют следующие источники дохода:
1. Изменение курса, наращение процента;
2. Наращение процента, дисконт;
3. Дисконт, наращение курса;
4. Двойная конверсия, дисконт.
1193124. Если ставку налога увеличить в два раза, то сумма процента:
1. Уменьшится в два раза;
2. Уменьшится в 1,444раза;
3. Увеличится в 1,444раза;
4. Увеличится в два раза.
1202134. Если ставку налога увеличить в два раза, то наращенная сумма:
1. Уменьшится в два раза;
2. Уменьшится в 1,444раза;
3. Увеличится в 1,444раза;
4. Увеличится в два раза.
Глава 2 Сложные проценты
