Глава 1 Простые проценты и простой дисконт
Оглавление
Введение 6
Глава 1 Простые проценты и простой дисконт 12
1.1 Процентные деньги и простой процент 12
1.2 Погашение задолженности частями 18
1.3 Наращение процентов в потребительском кредите 21
1.4 Дисконтирование по простым процентным ставкам. Наращение
по учетной ставке 21
1.5 Прямые и обратные задачи при начислении процентов
и операции дисконтирования по простым ставкам 25
1.6 Определение ссуды и величины процентной ставки 26
1.7 Конверсия валюты и наращение процентов 28
1.8 Тестовые задания 29
Глава 2 Сложные проценты 35
2.1 Сложные и непрерывно начисляемые проценты 35
2.2 Реальная и номинальная ставки 36
2.3 Формула сложных процентов 36
2.4 Эффективная ставка процентов 40
2.5Переменная ставка процентов 42
2.6 Непрерывное начисление процентов 43
2.7Определение срока ссуды и величины процентной ставки 44
2.8 Дисконтирование по сложной ставке 45
2.9 Сложные проценты, определение наращенной суммы
при внутригодовой капитализации 45
2.10 Тестовые задания 50
Глава 3 Уравнение эквивалентности 52
3.1 Датированные суммы 52
3.2 Серии датированных сумм 53
3.3 Эквивалентные серии платежей 55
3.4 Тестовые задания 60
Глава 4 Аннуитеты 63
4.1 Настоящая стоимость и итоговая сумма обыкновенного аннуитета 64
4.2 Полагающиеся аннуитеты 67
4.3 Отсроченные аннуитеты 71
4.4 Тождества, связывающие накопления и аннуитеты 73
4.5 Определение платежей аннуитета 75
4.6 Страховые аннуитеты 77
4.6.1 Финансовая эквивалентность в страховании 77
4.6.2 Таблицы смертности и страховые вероятности 80
4.6.3 Коммутационные функции 84
4.7 Тестовые задания 87
Глава 5 Фундаментальный анализ 91
5.1 Понятие фондового рынка, его участники и торговые площадки 91
5.2 Цели фундаментального анализа, его предмет и применяемые
методы 95
5.3 Факторы рынка акций, отраслевой анализ 106
5.4 Тестовые задания 113
Глава 6 Использование технического анализа для прогнозирования
биржевых цен 118
6.1 Основополагающие принципы технического анализа 118
6.2 Типы графиков движения рынка 119
6.3 Ценовой тренд, сопротивление и поддержка 122
6.4 Линии тренда и линии канала 125
6.5 Теория Доу 125
6.6 Числовая последовательность Фибоначчи 127
6.7 Теория Циклов 129
6.8 Индикаторы технического анализа 132
6.9 Тестовые задания 153
Заключение 156
Учебно-методическое обеспечение 158
Литература 158
Материально-техническое и информационное обеспечение
дисциплины 159
 Введение
Введение
В настоящее время возрос интерес к финансовой деятельности, но следует отметить, что культура финансовых расчетов страдает, особенно тогда, когда расчеты производятся при анализе платежей, различных во времени или составляющих потоки (последовательности, серии) регулярно повторяющихся выплат.
 Любая финансово-кредитная операция, инвестиционный проект или коммерческое соглашение предполагает наличие ряда условий их выполнения, с которыми согласны участвующие стороны. К таким условиям относятся следующие количественные данные: денежные суммы, временные параметры, процентные ставки и некоторые другие дополнительные величины. Каждая из перечисленных характеристик может быть представлена самым различным образом. Например, платежи могут быть единственными (разовыми) или в рассрочку, постоянными или переменными во времени.
Любая финансово-кредитная операция, инвестиционный проект или коммерческое соглашение предполагает наличие ряда условий их выполнения, с которыми согласны участвующие стороны. К таким условиям относятся следующие количественные данные: денежные суммы, временные параметры, процентные ставки и некоторые другие дополнительные величины. Каждая из перечисленных характеристик может быть представлена самым различным образом. Например, платежи могут быть единственными (разовыми) или в рассрочку, постоянными или переменными во времени.
Существует более десятка видов процентных ставок и методов начисления процентов. Время устанавливается в виде фиксированных сроков платежей, интервалов поступления доходов, моментов погашения задолженности и т. д. В рамках одной финансовой операции перечисленные показатели образуют некоторую взаимосвязанную систему, подчиненную соответствующей логике. Изменение значения одной из величин в системе обязательно отразится на результатах других показателей. Поэтому, такие системы должны являться объектом приложения количественного финансового анализа. Методы этого анализа составляют предмет финансовой математики (ФМ).
Количественный финансовый анализ предназначен для решения задач, которые можно разделить на две группы: традиционные или «классические» и новые, нетрадиционные, постановка и интенсивная работа которых ведется в последние два-три десятилетия.
Количественный финансовый анализ применяется как в условиях определенности, так и неопределенности. В первом случае предполагается, что данные для анализа заранее известны и фиксированы. Например, при выпуске обычных облигаций однозначно оговариваются все параметры – срок, купонная доходность, порядок выкупа. Во втором случае задача усложняется. Так как здесь приходится учитывать неопределенность – динамику денежного рынка (уровень процентной ставки, колебание валютного курса и т. д.), поведение контрагента.
Рамки ФМ простираются от элементарных начислений процентов до относительно сложных расчетов, например оценки влияния различных факторов на эффективность выпуска облигаций или методов сокращения рисков путем диверсификации портфеля финансовых инвестиций.
К основным задачам ФМ относятся:
- измерение конечных финансовых результатов операции (сделки, контракты) для каждой из участвующих сторон;
- разработка планов выполнения финансовых операций, в том числе планов погашения задолженности;
- измерение зависимости конечных результатов операции от основных ее параметров;
- оптимизация портфеля активов.
Данный перечень не является исчерпывающим. Область приложения методов количественного анализа финансовых операций регулярно расширяется. В последнее время большое внимание уделяется портфелям финансовых инвестиций и задолженности.
Знание методов, применяемых в ФМ, необходимо при непосредственной работе в любой сфере финансов и кредита, в том числе и па этапе разработки условий контрактов. Нельзя обойтись без них при финансовом проектировании, а также при сравнении и выборе долгосрочных инвестиционных проектов. Финансовые вычисления являются необходимой составляющей расчетов в долгосрочном личном страховании.
Научно-технический прогресс затронул важную область экономики такую как финансово-кредитные отношения. Многие новшества здесь тесно связаны с компьютеризацией финансово-банковской деятельности. Это позволило по-новому взглянуть на содержание финансово-кредитных операций и предложить клиентам новые виды услуг, выходящие за рамки традиционных. Это, в частности, новые инструменты денежно-кредитного рынка – опционы, соглашения о будущей процентной ставке и т. п.
В практических финансовых операциях суммы денег вне зависимости от их назначения или происхождения связываются с конкретными моментами или периодами времени. Для этого в контрактах фиксируются соответствующие сроки, даты, периодичность выплат и т. д. Необходимость учета временного фактора вытекает из сущности финансирования, кредитования и инвестирования и выражается в неравноценности денег, относящихся к разным моментам времени. Влияние фактора времени многократно усиливается в период инфляции.
Отметим, что в последнее время созданы новые технологии, совершенствующие саму финансово-кредитную деятельность. Такие технологии содержат в качестве одной из важных составляющих тот или иной метод ФМ. В качестве примера такого новшества можно указать на экспертные системы. Экспертная система кратко может быть определена как автоматизированная система, способная имитировать мышление специалиста и принимать решение в определенной узкой деятельности человека. Основное отличие экспертной системы от обычной автоматизированной системы обработки информации состоит в наличии развитого логического аппарата в виде набора правил "если ..., то ...". Правила формулируются и вводятся в систему непосредственно экспертами или с помощью самообучения системы путем множественных прогонов на ЭВМ реальных ситуаций.
При наличии множества видов кредитования фермеров и более 3 тыс. правил и условий их выдачи (пример простейшего правила: кредит открывают лицам не моложе 18 и не старше 60 лет) решение о кредитовании, включая правомерность его предоставления, размер, срок, продолжительность льготного периода, оказывалось весьма трудоемким. Применение экспертной системы позволило многократно сократить время принятия решений.
В практических финансовых операциях суммы денег вне зависимости от их назначения или происхождения, так или иначе связываются с конкретными моментами или периодами времени. Для этого в контрактах фиксируются соответствующие сроки, даты, периодичность выплат. Вне времени нет денег. Фактор времени, особенно в долгосрочных операциях, играет не меньшую, а иногда даже и большую роль, чем размеры денежных сумм. Необходимость учета временного фактора вытекает из сущности финансирования, кредитования и инвестирования и выражается в принципе неравноценности денег, относящихся к разным моментам времени или в другой формулировке — принципе изменения ценности денег во времени. Интуитивно понятно, что 1000 рублей, полученные через 5 лет, не равноценны этой же сумме, поступившей сегодня, даже, если не принимать во внимание инфляцию и риск их неполучения.
Влияние фактора времени многократно усиливается в период инфляции. Этот фактор часто лежит в основе явного или скрытого мошенничества и недобросовестности. Очевидным следствием принципа изменения ценности денег во времени является неправомерность суммирования денежных величин, относящихся к разным моментам времени, особенно при принятии решений финансового порядка. Однако такое суммирование вполне допустимо там, где фактор времени не имеет принципиального значения. Например, в бухгалтерском учете для получения итогов по периодам и в финансовом контроле. Неправомерно также и непосредственное сравнение разновременных денежных величин. Их сравнение допустимо только при "приведении" таких сумм к одному моменту времени.
Не менее важным в финансовом анализе является принцип финансовой эквивалентности. Под ним понимается равенство (эквивалентность) финансовых обязательств, участвующих в операции сторон. Ограничимся двумя иллюстрациями. Покупатель облигации выплачивает ее рыночную цену, а эмитент обязуется периодически выплачивать ему купонный доход и вернуть в конце срока сумму, равную номиналу облигации. Страхователь выплачивает стоимость страхования, а страховщик обязуется выплатить ему страховую сумму, но только при наступлении страхового события. В отличие от первого примера, где платежи обеих сторон безусловны, здесь платеж страховщика имеет вероятностный характер.
Принцип эквивалентности позволяет изменять условия контрактов без нарушения принятых обязательств. Согласно ему можно изменять уровень процентных ставок, их вид, сроки исполнения обязательств, распределение платежей во времени и т.д. (разумеется, с согласия контрагента) в рамках одной операции, не нарушая взаимной ответственности. На этом принципе основаны решения многих проблем.
Оба указанных выше принципа не могут быть реализованы без того или иного способа наращения процентов или дисконтирования с применением какого-либо вида процентной ставки. Можно выделить ряд признаков, по которым различаются процентные ставки.
Для начисления процентов применяют постоянную базу начисления и последовательно изменяющуюся (за базу принимается сумма, полученная на предыдущем этапе наращения и дисконтирования). В первом случае используют простые проценты, во втором – сложные процентные ставки, при применении которых проценты начисляются на проценты.
Важным является выбор принципа расчетов процентных денег. Существует два таких принципа: от настоящего к будущему и, наоборот, от будущего к настоящему. Соответственно применяют ставки наращения и дисконтные, или учетные, ставки. Процентные ставки могут быть фиксированными (в контракте указываются их размеры) или плавающими. В последнем случае указывается не сама ставка, а изменяющаяся во времени база (базовая ставка) и размер надбавки к ней — маржа.
Важное место в системе процентных ставок занимает ставка рефинансирования Центрального Банка России — ставка, по которой ЦБ выдает кредит коммерческим банкам.
Добавим, что при последовательном погашении задолженности возможны два способа начисления процентов. Согласно первому процентная ставка (простая или сложная) применяется к фактической сумме долга. По второму способу простые проценты начисляются сразу на всю сумму долга без учета последовательного его погашения. Последний способ применяется в потребительском кредите и в некоторых других (правда, редких) случаях.
В учебном пособии дается понятие о процентных деньгах, простых и сложных процентах, дисконтировании (учете изменения стоимости денег со временем в связи с возможностью получения процентов), эквивалентности платежей, аннуитетах (серия регулярных платежей). Эти понятия широко используются для описания элементов практической финансовой деятельности (оформление векселей и их купли-продажи, амортизация долгов, купля-продажа в рассрочку, расчет инвестиций), оперирование простейшими ценными бумагами – облигациями, определение их рыночной цены, амортизации и обесценивания оборудования, определения цены акций.
В работе рассматриваются примеры выполнения расчетов по различным темам финансовой математики. Пособие предназначено для студентов всех форм обучения изучающих курс финансовой математики.
Учебное пособие поможет студентам работать с математическими основами финансов и их применением для расчетов, считающихся обычными в странах с развитой финансовой культурой.
Студент, приступающий к изучению дисциплины «Финансовая математика», должен обладать соответствующими знаниями по дисциплинам «Математика» и «Экономическая теория». Знания методов финансовых вычислений являются базовыми для изучения таких дисциплин как: «Финансы», «Финансовый менеджмент», «Финансовый анализ», «Деньги, кредит, банки», «Рынок ценных бумаг».
С помощью этих методов осуществляется приведение денежных сумм, относящихся к различным временным периодам, к требуемому моменту времени в настоящем или будущем. При этом в качестве нормы приведения используется процентная ставка.
Под наращенной суммой ссуды (долга, депозита, других видов выданных в долг или инвестированных денег) понимают первоначальную ее сумму с начисленными процентами к концу срока начисления. Наращенная сумма определяется умножением первоначальной суммы долга на множитель наращения, который показывает, во сколько раз наращенная сумма больше первоначальной. Расчетная формула зависит от вида применяемой процентной ставки и условий наращения.
К наращению по простым процентам обычно прибегают при выдаче краткосрочных ссуд (на срок до 1 года) или в случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются. Для записи формулы наращения простых процентов примем обозначения;
I - проценты за весь срок ссуды;
P - первоначальная сумма ссуды;
S - наращенная сумма, т.е. сумма в конце срока ссуды;
i - ставка наращения процентов (десятичная дробь);
n - срок ссуды в годах.
Если срок ссуды измеряется в годах (как это обычно и бывает), то i означает годовую процентную ставку. Соответственно каждый год приносит проценты. Начисленные за весь срок проценты составят
I = Pni.
Наращенная сумма, таким образом, находится как
S = P + I = P + Pni = P (1 + ni). (1.1)
Выражение (1.1) называют формулой наращения по простым процентам или кратко — формулой простых процентов, а множитель (1 + ni) - множителем наращения простых процентов.
Пример 1. Определить проценты I и сумму накопленного долга S, если ссуда равна P=700 тыс.руб., срок 4 года, проценты простые по ставке 20% годовых (i= 0,2):
I = 700×4×0,2 = 560 тыс. руб.;
S = 700+560 = 1260 тыс. руб.
Увеличим теперь ставку в два раза. Сумма процентов при этом удвоится, а наращенная сумма увеличится в (1+2×4×0,2 ) /( 1+4×0,2 ) =1,444 раза.
Практика расчета процентов для краткосрочных ссуд.Поскольку процентная ставка, как правило, устанавливается в расчете за год, то при сроке ссуды менее года необходимо определить, какая часть годового процента уплачивается кредитору. Сходная проблема возникает и в случаях, когда срок ссуды меньше периода начисления.
Рассмотрим наиболее распространенный в практике случай — с годовыми периодами начисления. Очевидно, что срок ссуды необязательно равен целому числу лет. Выразим срок n в виде дроби
n=t/K, (1.2)
где t — число дней ссуды, К — число дней в году, или временная база начисления процентов. При расчете процентов применяют две временные базы: К =360 дней (12 месяцев по 30 дней) или К = 365/366 дней. Если К = 360, то получают обыкновенные или коммерческие проценты, а при использовании действительной продолжительности года (365, 366 дней) рассчитывают точные проценты. Число дней ссуды также можно измерить приближенно и точно. В первом случае продолжительность ссуды определяется из условия, согласно которому любой месяц принимается равным 30 дням. В свою очередь точное число дней ссуды определяется путем подсчета числа дней между датой выдачи ссуды и датой ее погашения. День выдачи и день погашения считаются за один день.
Итак, возможны и применяются на практике три варианта расчета простых процентов:
1.Точные проценты с точным числом дней ссуды. Этот вариант, естественно, дает самые точные результаты. Данный способ применяется центральными банками многих стран и крупными коммерческими банками, например, в Великобритании, США. В коммерческих документах он обозначается как 365/365;
2.Обыкновенные проценты с точным числом дней ссуды. Этот метод, иногда называемый банковским, распространен в межстрановых ссудных операциях коммерческих банков, во внутристрановых — во Франции, Бельгии, Швейцарии. Он обозначается, как 365/360.
3.Обыкновенные проценты с приближенным числом дней ссуды. Такой метод применяется тогда, когда не требуется большой точности, например при промежуточных расчетах. Он принят в практике коммерческих банков Германии, Швеции, Дании. Метод условно обозначается как 360/360.
Очевидно, что вариант расчета с точными процентами и приближенным числом дней ссуды лишен смысла и не применяется. Поскольку точное число дней ссуды в большинстве случаев, больше приближенного (в чем легко убедиться, определив среднее за год число дней в месяце, которое равно 30,58), то метод начисления процентов с точным числом дней ссуды обычно дает больший рост, чем с приближенным.
В России, применяются как обыкновенные (360/360), так и точные проценты (365/365). В частности, точные проценты используются в официальных методиках ЦБР и МФ РФ для расчета доходности по государственным обязательствам. Начисление по формуле точных процентов требует определения фактического числа дней проведения операции, которое осуществляется по специальным справочным таблицам. Обыкновенные проценты в России используются в основном при проведении операций с векселями.
Применение специальных функций ППП EXCEL позволяет реализовать любой из известных в мировой практике методов начисления процентов, и освобождают аналитика от необходимости использования различных справочных материалов.
Пример 2. Ссуда в размере 1 млн. руб. выдана 20.01 до 05.10 включительно под 18% годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? При решении применим все три метода. Предварительно определим число дней ссуды: точное — 258, приближенное — 255.
1. Точные проценты с точным числом дней ссуды (365/365):
S = 1000 000(1 +(258/365)0,18) = 1 127 233 руб.
2. Обыкновенные проценты с точным числом дней ссуды (365/360):
S = 1000 000(1 + (258/360)0,18) = 1 129 000 руб.
3. Обыкновенные проценты с приближенным числом дней ссуды (360/360):
S = 1000 000(1 + (255/360)0,18) = 1 127 500 руб.
Если общий срок ссуды захватывает два смежных календарных года и есть необходимость в делении суммы процентов между ними ( например, при определении годовых сумм доход и т.д.), то общая сумма начисленных простых процентов составит сумму процентов, полученных в каждом году:
I= 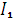 +
+ 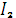 = P
= P 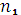 i+P
i+P 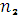 i,
i,
Здесь 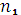 и
и 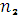 - части срока ссуды, приходящиеся на каждый календарный год.
- части срока ссуды, приходящиеся на каждый календарный год.
Переменные ставки.
В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки. Если это простые ставки, то наращенная на конец срока сумма определяется следующим образом:
S=P(1+ 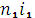 +
+ 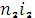 +…+
+…+ 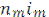 ) (1.3)
) (1.3)
где 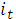 — ставка простых процентов в периоде t;
— ставка простых процентов в периоде t;
n t— продолжительность периода с постоянной ставкой 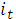 .
.
Пример 3. Контракт предусматривает следующий порядок начисления процентов: первый год— 16%, в каждом последующем полугодии ставка повышается на 1%. Необходимо определить множитель наращения за 2,5 года. Находим
I = 1+1×0,16+0,5×0,17+0,5×0,18+0,5×0,19=1,43.
Начисление процентов при изменении сумм депозита во времени.Принципиально ничего не меняется, если сумма, на которую начисляются проценты, изменяет свою величину во времени (размер вклада на сберегательном счете, текущий счет при периодическом его пополнении или снятии денег и т.п.). В этом случае
I= 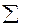 Rj nj i, (1.4)
Rj nj i, (1.4)
где Rj— остаток средств на счете в момент j после очередного поступления или списания средств, nj— срок хранения денег (в годах) до нового изменения остатка средств на счете.
В банковско-сберегательном деле обычно применяют следующий способ, основанный на преобразовании (1.4). Для этого измерим интервалы между моментами изменений величины остатка на счете в днях, а процентную ставку выразим в процентах (а не в десятичных дробях как выше). После чего получим
I= 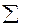 Rj*nj*i=(
Rj*nj*i=( 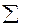 Rj*tj/100)/(K/i) (1.5)
Rj*tj/100)/(K/i) (1.5)
Как и прежде К означает число дней в году, a tj- срок в днях между последовательными изменениями остатков на счете.
Величину 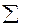 Rj*tj/100 называют процентным числом, а делитель — процентным (или постоянным) делителем.
Rj*tj/100 называют процентным числом, а делитель — процентным (или постоянным) делителем.
Пример 4. Движение средств на счете характеризуется следующими данными: 05. 02 поступило 12 млн. руб., 10.07 снято 4 млн. руб. и 20.10 поступило 8 млн. руб. Найти сумму на счете на конец года. Процентная ставка 18% годовых. Процентный делитель составит 365 : 18 = 20,27778. Расчет суммы процентных чисел приведен в следующей таблице.
| Дата | Движение Средств (млн. руб.) | Остаток Rj (млн. руб.) | Срок tj (дни) | Процентное число |
| 05.02 | 18,6 | |||
| 10.07 | - 4 | 8,16 | ||
| 20.10 | 11,52 | |||
| 31.12 | - | - | - | |
| Итого | 38,28 |
Сумма процентов за весь срок равна 38,28/20,27778=1,888 (млн. руб.).
Реинвестирование по простым ставкам.В практике, при инвестировании средств в краткосрочные депозиты, иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока. Фактически это означает реинвестирование средств, полученных на каждом этапе наращения, с помощью постоянной или переменной ставок. Наращенная сумма для всего срока составит в этом случае
S=P(1+n1*i1)(1+n2*i2)..(1+nt*it). (1.6)
где it— размер ставок, по которым производится реинвестирование.
Если промежуточные сроки начисления и ставки не изменяются во времени, то вместо (1.6) имеем
S=P(1+n*i)m, (1.7)
где m- количество повторений реинвестирования.
Пример 5. 100 млн. руб. положены 1-го января на месячный депозит под 20% годовых. Какова наращенная сумма, если операция повторяется 3 раза? Если начислять точные проценты (365/365), то
S= 100(1+(31/365)0,2)(1+(28/365)0,2)(1+31/365)0,2)=105,013 (млн. руб.)
Начисление обыкновенных процентов (360/360) при реинвестировании дает
S= 100(1+(30/360)*0,2)3= 105,084 (млн. руб.)
Глава 2 Сложные проценты
Формула сложных процентов
В финансовой практике значительная часть расчетов ведется с использованием схемы сложных процентов.
Применение схемы сложных процентов целесообразно в тех случаях, когда:
-проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов.
Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга:
S = P+ I = P + P• i = P • (1 + i)– за один период начисления;
S = (P + I) • (1 + i) = P • (1 + i) • (1 + i) = P• (1 + i)2
– за два периода начисления; отсюда, за n периодов начисления формула примет вид: S= P (1 + i)n = P kн , где
S – наращенная сумма долга;
P – первоначальная сумма долга;
i – ставка процентов в периоде начисления;
n – количество периодов начисления;
kн – коэффициент (множитель) наращения сложных процентов.
Эта формула называется формулой сложных процентов.
Различие начисления простых и сложных процентов в базе их начисления. Если простые проценты начисляются все время на одну и ту же первоначальную сумму долга, т.е. база начисления является постоянной величиной, то сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу. Таким образом, простые проценты по своей сути являются абсолютными приростами, а формула простых процентов аналогична формуле определения уровня развития изучаемого явления с постоянными абсолютными приростами. Сложные проценты характеризуют процесс роста первоначальной суммы со стабильными темпами роста, при наращении ее по абсолютной величине с ускорением, следовательно, формулу сложных процентов можно рассматривать как определение уровня на базе стабильных темпов роста.
Согласно общей теории статистики, для получения базисного темпа роста необходимо перемножить цепные темпы роста. Поскольку ставка процента за период является цепным темпом прироста, то цепной темп роста равен: (1 + i).
Тогда базисный темп роста за весь период, исходя из постоянного темпа прироста, имеет вид: (1 + i)n.
Базисные темпы роста или коэффициенты (множители) наращения, зависящие от процентной ставки и числа периодов наращения, табулированы и представлены в Приложении 2. Экономический смысл множителя наращения состоит в том, что он показывает, чему будет равна одна денежная единица (один рубль, один доллар и т.п.) через n периодов при заданной процентной ставке i.
При краткосрочных ссудах начисление по простым процентам предпочтительнее, чем по сложным процентам; при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам значительно выше, чем по простым.
При любом i,
если 0 < n < 1, то (1 + ni) > (1 + i)n ;
если n > 1, то (1 + ni) < (1 + i)n ;
если n = 1, то (1 + ni) = (1 + i)n .
Таким образом, для лиц, предоставляющих кредит:
-более выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года);
-более выгодной является схема сложных процентов, если срок ссуды превышает один год;
-обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.
Пример 1. Сумма в размере 2'000 руб. дана в долг на 2 года по ставке процента равной 10% годовых. Определить проценты и сумму, подлежащую возврату.
Решение:
Наращенная сумма
S= P • (1 + i)n = 2'000 • (1 + 0,1)2 = 2'420 руб.
или
S = P • kн = 2'000 • 1,21 = 2'420 руб.,
где kн = 1,21
Сумма начисленных процентов
I = S - P = 2'420 - 2'000 = 420 руб.
Таким образом, через два года необходимо вернуть общую сумму в размере 2'420 руб., из которой 2'000 руб. составляет долг, а 420 руб. – "цена долга".
Достаточно часто финансовые контракты заключаются на период, отличающийся от целого числа лет.
В случае, когда срок финансовой операции выражен дробным числом лет, начисление процентов возможно с использованием двух методов:
-общийметод заключается в прямом расчете по формуле сложных процентов:
S = P • (1 + i)n, n = a + b,
где n– период сделки;
a– целое число лет;
b – дробная часть года.
-смешанный метод расчета предполагает для целого числа лет периода начисления процентов использовать формулу сложных процентов, а для дробной части года – формулу простых процентов:
S= P• (1 + i)a • (1 + bi).
Поскольку b < 1, то (1 + bi) > (1 + i)a, следовательно, наращенная сумма будет больше при использовании смешанной схемы.
Пример 2. В банке получен кредит под 9,5% годовых в размере 250 тыс. руб. со сроком погашения через два года и 9 месяцев. Определить сумму, которую необходимо вернуть по истечении срока займа двумя способами.
Решение:
Общий метод:
S= P • (1 + i)n = 250 • (1 + 0,095)2,9 = 320,87 тыс. руб.
Смешанный метод:
S = P• (1 + i)a • (1 + bi) =
= 250 • (1 + 0,095)2 • (1 + 270/360 • 0,095) =
= 321,11 тыс. руб.
Таким образом, по общему методу проценты по кредиту составят
I = S - P = 320,87 - 250,00 = 70,84 тыс. руб.,
а по смешанному методу
I = S - P = 321,11 - 250,00 = 71,11 тыс. руб.
Как видно, смешанная схема более выгодна кредитору.
Переменная ставка процентов
Необходимо отметить, что основная формула сложных процентов предполагает постоянную процентную ставку на протяжении всего срока начисления процентов. Однако, предоставляя долгосрочную ссуду, часто используют изменяющиеся во времени, но заранее зафиксированные для каждого периода ставки сложных процентов. В случае использования переменных процентных ставок, формула наращения имеет следующий вид:
S=P(1+i1)n1(1+i2)n2 • • • (1+ik)nk
где ik – последовательные во времени значения процентных ставок;
nk – длительность периодов, в течение которых используются соответствующие ставки.
Пример 5.Фирма получила кредит в банке на сумму 100'000 руб. сроком на 5 лет. Процентная ставка по кредиту определена в 10% для 1-го года, для 2-го года предусмотрена надбавка к процентной ставке в размере 1,5%, для последующих лет 1%. Определить сумму долга, подлежащую погашению в конце срока займа.
Решение:
Используем формулу переменных процентных ставок:
S = P • (1 + i1)n1 • (1 + i2)n2 • … • (1 + ik)nk =
= 100'000 • (1 + 0,1) • (1 + 0,115) • (1 + 0,11)3 =
= 174'632,51 руб.
Таким образом, сумма, подлежащая погашению в конце срока займа, составит 174'632,51 руб., из которых 100'000 руб. являются непосредственно суммой долга, а 74'632,51 руб. – проценты по долгу.
Датированные суммы
Использование значений денежных сумм без указания даты, когда они должны использоваться, является бессмысленным. Очевидно, что 1000 руб. наличными в настоящее время предпочтительнее, чем 1500 руб., которые вы получите через 50 лет. Сумма платежа вместе с датой погашения называется датированной суммой.
В общем случае датированные суммы сравниваются по следующему правилу эквивалентности: сумма Р, полагающаяся на данную дату, эквивалентна при данной норме сложного процента i сумме S , полагающейся нап периодов конверсии позже, если является справедливым хотя бы одно из следующих равенств:
S=P(1+i)n или P=(1+i)-n S
Таким образом, накопление или дисконтирование могут рассматриваться как простое преобразование заданной датированной суммы к другой дате. Преобразование делается в соответствии со следующей временной диаграммой:
 ΩΩΩ
ΩΩΩ
Прошлая и будущая суммы эквивалентны датированной сумме D.
Важным и полезным свойством эквивалентных датированных сумм является свойство 1: при данной норме сложного процента если А эквивалентно В и В эквивалентно С, то А эквивалентно С.
Для доказательства этого утверждения мы расположим данные на временной диаграмме следующим образом:
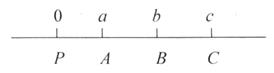
где 0 означает настоящее время и а, b, с представляют числа периодов конверсии от настоящего времени до соответствующих дат погашения.
Если А эквивалентно В, то B=A(1+i)b-a
Если В эквивалентно С, то C=(1+i)c-b B
Исключая из этих равенств сумму В, получим, что:
C=A(1+i)b-a(1+i)c-b=A(1+i)c-a
Полученный результат является условием эквивалентности датированных сумм А и С.
Это свойство не имеет места для норм простого процента и норм простого дисконта. Поэтому понятие эквивалентности для этих норм не применяется.
Серии датированных сумм
Сумма двух или большего числа датированных сумм, погашаемых в различные даты, практически не имеет смысла. Например, предположим, что 20000 руб. погашается через два года, а 30000 руб. погашается через пять лет. Сумма 20000 + 30000 = 50000 руб. не связана, с какой либо датой и поэтому мало о чем говорит. Однако если все рассматриваемые суммы преобразовать в эквивалентные датированные суммы с одной и той же датой погашения, то сумма таких эквивалентных сумм приобретает смысл и называется датированной суммой серии. Она будет изменяться в зависимости от даты, к которой преобразованы эквивалентные суммы. Для различных датированных сумм одной и той же серии справедливо следующее свойство 2: датированные суммы одной и той же серии, определенные для различных дат, являются эквивалентными.
Пусть А и В будут двумя датированными суммами, погашаемыми через а и b периодов начисления от настоящего времени. Пусть также U и V будут двумя датированными суммами этой серии, определенными для дат u и v (за единицу времени принимается период начисления). Представим эти данные на временной диаграмме:
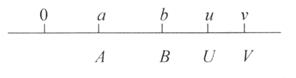
Преобразовывая значения А и В ко времени и согласно правилу эквивалентности и суммируя результаты, получим датированную сумму серии, погашаемую через u периодов:
U=A(1+i)u-a+B(1+i)u-b
Умножая обе части этого равенства на (1+i)v-u и производя очевидные упрощения, получим другую датированную сумму серии, погашаемую уже через v периодов начисления,
