Порядок расчета величины лизингового платежа

Для всех лизинговых схем исходным требованием является равенство современной стоимости потока лизинговых платежей затратам на приобретение оборудования.

Схема А. Регулярные постоянные платежи, сложные проценты.

В преобладающем большинстве случаев поток лизинговых платежей представляет собой постоянную ренту. Соответственно методы расчетов периодических лизинговых платежей базируются на теории постоянных финансовых рент.

Примем следующие обозначения:

R - размер постоянного платежа;

n – срок лизинга в месяцах, кварталах, годах (общее число платежей) (как правило в лизинговом контракте число платежей равно числу начислений процентов);

r - процентная ставка за период (норма доходности);

S – доля остаточной стоимости в первоначальной стоимости оборудования.

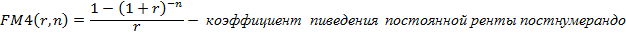
Если платежи постоянны во времени и погашают всю стоимость имущества, то при выплатах постнумерандо стоимость имущества для лизингодателя будет определяться по формуле:

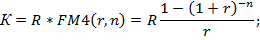
откуда:

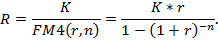
В некоторых схемах для упрощения расчетов размеров платежей можно применить коэффициент рассрочки платежей, определяющие долю стоимости оборудования, погашаемую пи каждой выплате:

Коэффициент рассрочки для постоянных рент постнумерандо при условии, что применяются сложные проценты равен:

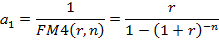
Коэффициент рассрочки для выплат пренумерандо равен:

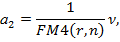
где ν – дисконтный множитель по ставке r,

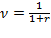
Размеры лизинговых платежей определяются путем умножения показателя стоимости имущества на коэффициент рассрочки:

R=K*a₁₍₂₎

Пусть первый платеж будет в k раз больше остальных (соответственно сокращается число остальных платежей). Тогда условие финансовой эквивалентности обязательств удовлетворяется следующими равенствами:

- для выплат постнумерандо:

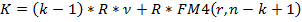
- для выплат пренумерандо:

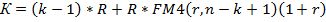
На основе этих равенств находятся необходимые значения лизинговых платежей:

- для выплат постнумерандо:

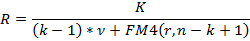
- для выплат пренуменрандо:

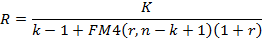
Пусть условием лизингового соглашения предусматривается выплата аванса (А). В этом случае уравнение эквивалентности будет иметь вид:

- для рент постнумерандо:

К=А+R*FM4(r,n)

- для рент пренумерандо:

К=А+R*FM4(r,n)(1+r)

Для расчета R применяются коэффициенты рассрочки.

R=(K-A)*а₁₍₂₎

Если лизинговый контракт предусматривает выкуп имущества по остаточной стоимости, доля которой в стоимости имущества равна S, то уравнение эквивалентности имеет вид:

- при платежах постнумерандо:

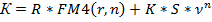
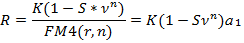
- при платежах пренумерандо:

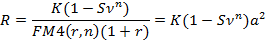
Если одновременно учитывается авансовый платеж и выкуп имущества уравнения эквивалентности будут иметь вид:

- для выплат постнумерандо:

К(1-Sνⁿ)=A+R*FM4(r,n)

- для выплат пренумерандо

К(1- Sνⁿ)=A+R*FM4(r,n)(1+r).

Размеры лизинговых платежей будут определяться по формуле:

- для выплат постнумерандо:

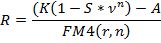
- для выплат пренумерандо:

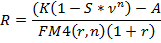
Вторая задача – деление суммы платежа по лизингу (R) на сумму амортизации долга и выплату процентов.

Сумма, идущая на погашение основного долга, находится как разность лизингового платежа и процентов на остаток задолженности.

1. Платежи постнумерандо

d_t=R-D_t-1*r, t=1, … ,n;

где d_t – сумма погашения основного долга в периоде t;

D_t-1 – остаток долга на конец периода t-1.

D₀=К.

- в первом периоду d₁=R-K*r.

Остаток задолженности последовательно определяется как

D_t=D_t-1-d_t

1. Платежи пренумерандо

d₁=R, d₂=R-K*r,d_t=R-D_t-1*R

Схема Б. Регулярные постоянные платежи

Исходное требование: величина платежа определяется размером сумм погашения основного долга и выплат процентов. Расчет выполняется по схеме погашения задолженности равными долями (суммами) (см. разд. 11.1).

Для схемы с полным погашением стоимости

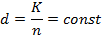
Платежи по лизингу в конце периода t определяются по формуле

R_t = D_t-1*r+d

где R_t – размер лизингового платежа в периоде t.

Остаток долга на конец периода последовательно находится как разность D_t=D_t-1-d

Cхема А. Нерегулярные платежи

Задается график лизинговых платежей (сроки и суммы). Сбалансированность выплат и задолженности достигается при определении размера последней выплаты. Исходное равенство имеет вид:

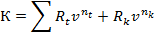
где R_t, n_t – сумма и срок t-го платежа;

R_k, n_k - сумма си срок последнего платежа.

Деление суммы платежа на проценты за кредит и суммы, погашающие основной долг, производится последовательно по формуле:

D_t=R_t-D_t-1*r

Схема Б. Нерегулярные платежи

Задается график погашения основного долга. Проценты за кредит последовательно начисляются на остаток задолженности.